Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997. – 190 с.

2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.

Л 57 екция 9. Дифференциал функции

Цель лекции: изучить понятие дифференциала; понять его геометрический смысл; научиться применять дифференциал в приближенных вычислениях.

План лекции

1. Понятие дифференциала и его геометрический смысл

2. Дифференциал сложной функции

3. Дифференциалы высших порядков

4. Применение дифференциалов к приближенным вычислениям

5. Векторная функция скалярного аргумента и ее дифференциал

6. Дифференциал длины дуги

Введение

Ранее производные функций рассматривались как мгновенная скорость роста, то есть узнавали, во сколько раз быстрее растет функция по отношению к росту аргумента в точке. Дифференциал функции, хотя и имеет общие правила с производной в их нахождении, однако несет совершенно другой геометрический смысл, а именно: происходит не приращение функции, а приращение касательной. Это свойство используется в приближенных вычислениях, поскольку вычислить текущее значение функции прямой линии проще, чем исходной функции.

Отдельно рассматривается понятие векторной функции. В силу ограниченности объема курса это понятие дается в рамках одного вопроса. Однако его понимание и дифференциала векторной функции необходимо при изучении тем: «Векторный анализ», «Интегральное исчисление» и др. Подобные функции встречаются практически во всех прикладных задачах на траекторию движения. Отдельно отметим важность понятий дифференциала функции в теме «Дифференциальные уравнения».

1. Понятие дифференциала и его геометрический смысл

1.1. Дифференциал функции

ПРИМЕР 1.

Для при приращении на определить .

Решение.

Таким образом, состоит из двух частей (линейной и нелинейной) относительно .

Пусть дифференцируема в некоторой точке , следовательно, существует или , следовательно, по второму определению предела – бесконечно малая величина в точке . Выразим

, (1)

п

58

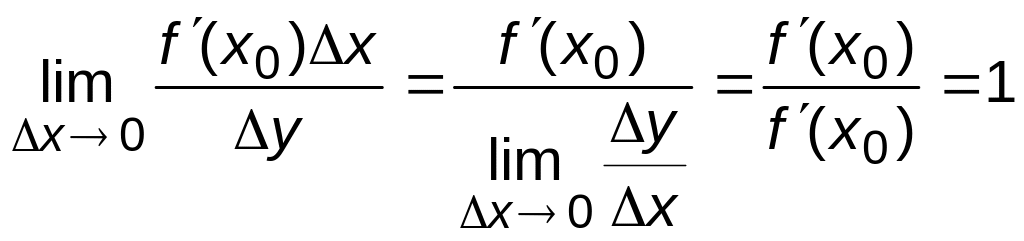ри следует, что . Сравним первое слагаемое с : . Следовательно ~ . Сравним второе слагаемое с : . Второе слагаемое (1) стремится к нулю быстрее, чем и даже . Обозначают .

Определение 1.

Главная, или линейная относительно , часть бесконечно малого приращения функции называется дифференциалом функции. Обозначается .

По определению . Для любых дифференциал определяется как . Если , то = , или

. (2)

Согласно определению 1 и выражению (2) дифференциал функции определяется как

, (3)

т. е. произведение производной этой функции на дифференциал независимой переменной. Из этого следует, что все формулы производных можно перенести на дифференциал.

1.2. Геометрический смысл дифференциала

Пусть – дифференцируемая функция. Обозначим через некоторую точку на кривой (рис. 1), приращение – через , тогда вторую точку, образованную этим приращением на кривой, обозначим . В обозначим угол . Определим = , или .

Д

59

ругими словами, дифференциал функции в точке, с геометрической точки зрения, есть приращение функции касательной в точке, тогда как приращение функции есть приращение ординаты точки графика. На рис. 1 видно, что . Очевидно, что для функции приращение касательной равно приращению функции в точке , поскольку касательная у функции совпадает с самой функцией.

ПРИМЕР 2.

Найти для . Имеем .