1.3. Лангранж теоремасы

Лангранж теоремасы (функцияның ақырғы өсімшелері туралы). Егер f(x) функциясы сегментінде үзіліссіз және ең болмағанда интервалында туындысы f´(x) ақырлы болса, ол интервалдың ішіндегі ең болмағанда бір c нүктесінде

теңдігі орындалады.

Дәлелдеу. егментінде қарастыратын мына көмекші функцияны алалық:

Ф(x) = f(c) – f(a) -

f(x) пен x-a функциялары сегментінде үзіліссіз, ең болмағанда интервалында ақырлы туындылары бар функциялар болғандықтан, сонымен бірге:

Ф(a) = f(a) – f(a) -

және

Ф(b) = f(b) – f(a) –

болуы себепті (7) көмекші функция Ролль теоремасының шарттарын түгелдей қанағаттандыратын болып шықты. Ендеше интервалының ішінде болатын ең болмағанда бір c нүктесі табылып, ол нүктеде Ф´(c) = 0 болады.

Бірақ:

Ф´(x) = f´(x) –

Сондықтан:

Ф´(c) = f´(c) –

яғни

Геометриялық мағынасы: y = f(x) графигі бойында A (a; f(a)) және B (b; f(b)) нүктелері арасынан C (c; f(c)) , a нүктесі табылып, графикке осы нүктедегі жанама АВ хордасына параллель болады (2-сурет).

у

Т

С

в

f(b)-f(a)

А

в-а

0 а с в х

2-сурет

f(b) – f(a) = f´(c) (b-a), a теңдігі Лагранж формуласы немесе ақырлы өсімше формуласы деп аталады. Оны кейде мынадай түрлерде қолданған тиімді:

f(b) – f(a) = f´(a + ) (b - a)

немесе

f(x+ ) – f(x) = f´(x + ) 0

Лагранж формуласының толып жатқан қолданылуының бір дербес жағдайына тоқталайық.

Теорема. Егер f(x) функциясы нүктесінде үзіліссіз болса және сол нүктеде не ақырлы , не ақырсыз шек

x

бар болса, туынды f´( ) те бар және осы шекке тең болады.

Дәлелдеу. Дәлелдемек болып отырған теоремада f(x) функциясы Лагранж теоремасының шарттарын түгелдей қанағаттандыратын болғандықтан үшін:

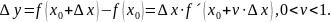
Бұдан:

Егер

деп белгілеп, v -ның шенелген шама екенін еске алсақ, және x –да (x )

x

яғни f´( ) бар болады, сонымен бірге

f´

x

теңдігі орындалады.

Ескерту. Лагранж теоремасының геометриялық түсініктемесін былай көрсетіп және

tg

түрінде дәлеледеуге болады.

Қисық бойынан бір нүктесі табылады, ал ол нүктедегі жанама хордаға параллель болады.

Мысалдар. 1-мысал. f(x) = lnx функциясына аралығында Лагранж формуласын қолданыңыз және сәйкес c нүктесін табыңыздар.

Шешуі. Функция берілген аралықта үзіліссіз дифференциалданады. c нүктесін f´(c) = теңдігінен табамыз: c =

2-мысал. параболасының нүктелері берілген (3-сурет). Жанама АВ хордасына параллель болатындай АВ доғасынан С нүктесін табу керек.

Шешуі. кесіндісінде берілген функциясы Лагранж теоремасының шарттарын қанағаттандырады.

Шарт бойынша:

Берілгендерді (6) Лагранж формуласына қойып, мыналарды аламыз:

Бұдан, мұндағы

Берілген функцияның туындысының болғандағы мәнін анықтаймыз:

бұдан,

Сонымен, нүктесінде жанама АВ хордасына параллель болады.

у В

Т

А

С

0 х

3-сурет