Мазмұны

Кіріспе

І бөлім.

1.1. Ферма теоремасы

1.2. Ролль теоремасы

1.3. Лангранж теоремасы

1.4. Коши теоремасы

II бөлім.

1.5. Орташа мәндер туралы теоремаларға қатысты жаттығулар

III бөлім.

Қорытынды

Пайдаланған әдебиеттер тізімі

К І Р І С П Е

Жоғары оқу орнындағы оқу процесінде де , мектеп математикасы курсында да дифференциал ұғымы негізгі ұғымдардың біріне жатады.

Анықтама. y = f(x) функциясының нүктесіндегі мәні өсімшесіне сәйкес өсімшесі мына түрде

(1)

жазылатын болса, онда f(x) функциясы нүктесінде дифференциалданады дейді. Мұндағы A дегеніміз –ке тәуелсіз қандай болса да бір сан, ал болса –тің функциясы және ол жағдайда –пен салыстырғанда жоғары ретті ақырсыз кіші шама.

Функцияның қандай болса да бір нүктеде дифференциалданатын болуы оның сол нүктеде ақырлы туындысының бар болуымен мәндес болып шығады. Сондықтан, функция туындысын табу амалын оны дифференциалдау деп те атайды. Дифференциалданатын функциялар төңірегінде дифференциалданатын функциялардың орта мәндері туралы теоремалар қарастырылады. Олардың қатарына: Ферма теоремасы, Ролль теоремасы, Лангранж теоремасы, Коши теоремасы жатады. Ферма мен Ролль теоремаларын функция туындысының түбірі туралы теоремалар деп те атайды. Пьер Ферма (1601-1665) – аты ақырсыз кішкенелер анализінің тарихы алдындағы кезеңімен тығыз байланысты Францияның көрнекті математигі. Мишель Ролль (1652-1719) – Франция математигі. Біраз уақыт дифференциалдық және интегралдық есептеуге қарсы болған кісі. Ол өзінің теоремасын тек алгебралық көпмүшеліктер (х-тің дәрежесі бойынша ) үшін ғана айтып кеткен. Ал Лагранж және Коши теоремаларын шектелген өсімшелер формуласы деп те атайды. Жозеф-Луи Лагранж (1736-1813) – Францияның үздік математигі және механигі. Августин-Луи Коши (1789-1857) - француз математигі.

Қарастырылатын Ролль, Лагранж, Коши теоремаларында туындының аргументі тәуелсіз айнымалының қандай болса да бір орташа с мәні болып табылады. Сондықтан туындылардың сәйкес мәндерін де орташа деп, ал сол аталған теоремаларды “орташа мәндер теоремалары” дейді.

І Бөлім

1.1. Ферма теоремасы

Ферма теоремасы : Егер функциясы :

1) сегментінде анықталған болса;

2) сол сегменттің ішкі c нүктесінде не ең үлкен, не ең кіші мәнін қабылдаса;

3) c нүктесінде ақырлы туынды  f ′ (c) бар болса;

Онда міндетті түрде f ′ (c) =0 .

Дәлелдеу. функциясы c нүктесінде ең кіші мәнін қабылдайды деп жорылық. Олау деу : барлық х - тер үшін

f(c) ≤ f(x)

арақатынасы орындалады деу болып табылады.

Егер x>c болса,

Бұдан

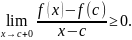(1)

Ал x<c болса,

онан:

(2)

Теореманың шарты бойынша :

(3)

Бұл соңғы шек x шамасы с нүктесінде қай жағынан ұмтылса да бірдей, яғни (3) шектің мәні х-тің с нүктесіне бір жағынан ұмтылуына тәуелді емес.

Демек, (1) мен (2) арақатынастарды бірге қарастырсақ, онда: f'(c)=0 болуға тиіс, дәлелдеу керегі де осы еді. Егер f(x) функциясы с нүктесінде өзінің ең үлкен мәнін қабылдайтын жағдайда да Ферма теоремасы осы сияқты дәлелденеді.

Ескертулер: 1. Теоремадағы с нүктесі сегментінің ішкі нүктесі болуы керек деген шарт өте маңызды шарт, өйткені ол шарт орындалмаса, теорема дұрыс болмайды. Неге десеңіз, сегментте берілген және ол сегменттің шеткі нүктелерінің бірінде ең үлкен, не ең кіші мәндерінің бірін қабылдайтын, сонымен бірге сол шеттік нүктеде туындысы бар, бірақ ол туынды нольге тең болмайтын функциялар толып жатыр.

2. Теореманы дәлелдеген уақытта f(x) функциясының c нүктесіндегі туындысы ақырсыздыққа айналмайтынына көзіміз жетті. Ендеше, теореманың формулировкасында «ақырлы туындысы бар» деудің орнына деудің орнына «туындысы бар» десе де болады.

Геометриялық мағынасы: y = f(x) функциясы графигінің нүктесіндегі жанамасы абцисса осіне параллель болады (8.1-сурет ).

8.1-сурет

Мысал: f(x)= функциясы [ 0, ] аралығында Ферма теоремасының шарттарын қанағаттандыра ма?

Шешуі. Жоқ, себебі: функция [ 0, ] кесіндісінде кемиді. Сондықтан өзінің ең үлкен мәнін х = 0, ең кіші мәнін х = нүктелерінде, яғни аралықтың шеткі (ішкі емес) нүктелерінде қабылдайды. Демек, Ферма теоремасы қолданылмайды:

f'