Ещё пример задания:
P-27. Сколько различных решений имеет система логических уравнений
(x1 x2) (x1 x2 x3) (x1 y1) = 1
(x2 x3) (x2 x3 x4) (x2 y2) = 1
…
(x6 x7) (x6 x7 x8) (x6 y6) = 1
(x7 x8) (x7 y7) = 1
x8 y8 = 1
где x1, …, x8, y1, …, y8, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (вариант 1, использование свойств битовых цепочек, М.А. Ройтберг):
перепишем систему с более понятными обозначениями:
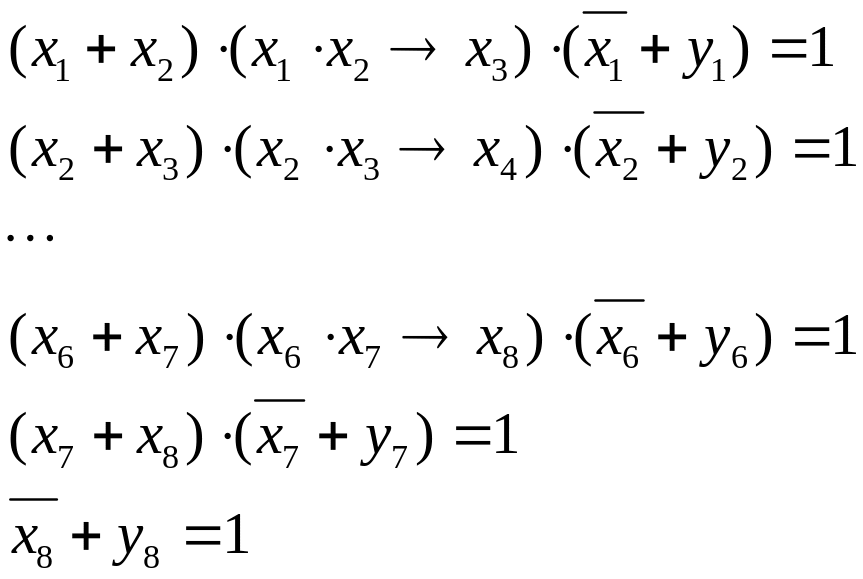
первые 6 уравнений однотипны, отличаются только сдвигом номеров переменных
будем рассматривать каждое решение как пару битовых цепочек (цепочек нулей и единиц)
и
первые сомножители в первых уравнениях,
,
означают, что в цепочке
не может быть двух нулей подряд (иначе
эта скобка в первых 6 уравнениях и всё
произведение равны нулю)вторые скобки,
,
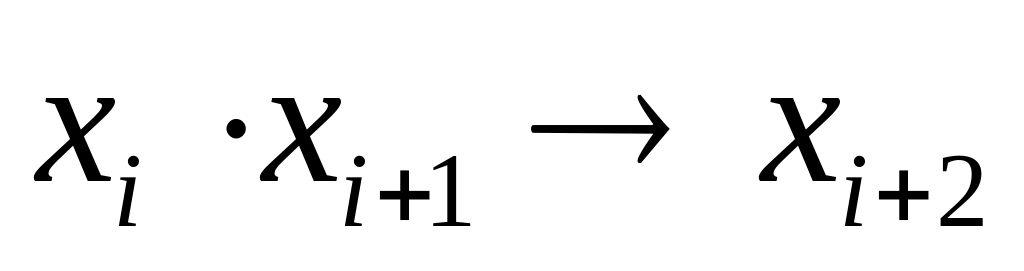означают, что если в цепочке
встретились две единицы подряд, то
потом будут только единицы, поскольку
в противном случае
и все произведение равно 0пока «забудем» про третьи сомножители (
);
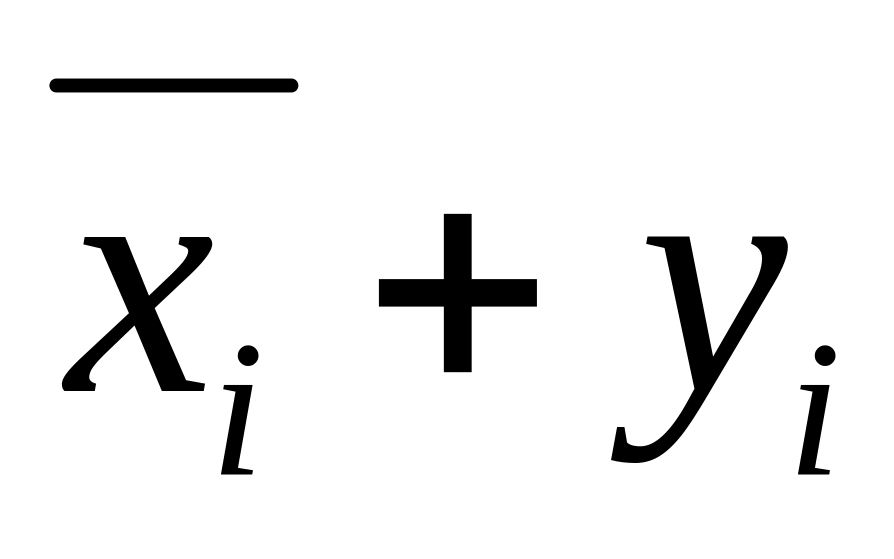тогда цепочка
в любом решении выглядит так: сначала
чередуются нули и единицы, а с некоторого
места идут только единицытакая цепочка полностью определяется позицией последнего нуля, т.е. есть всего 9 таких цепочек (позиция последнего нуля от 0 до 8, 0 значит, что нулей нет)
X0 = 11111111
X1 = 01111111
X2 = 10111111
X3 = 01011111
X4 = 10101111
X5 = 01010111
X6 = 10101011
X7 = 01010101
X8 = 10101010
третий сомножитель в каждом выражении – это импликация
это означает, что если ( ,
)
– решение и
,
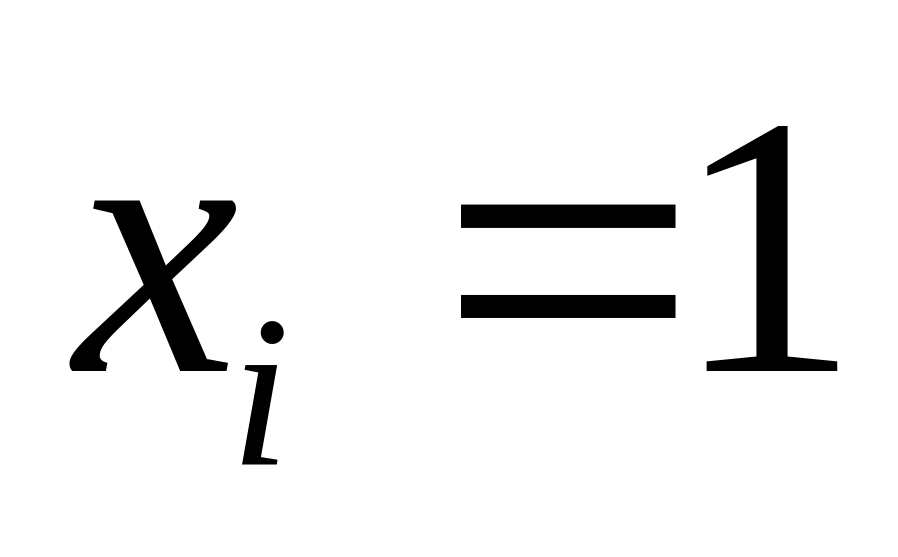то
;
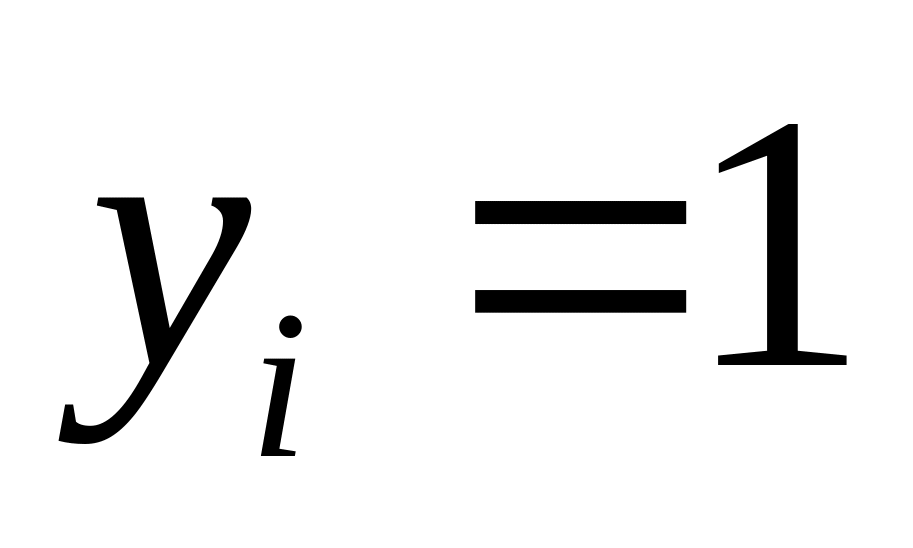если же
,
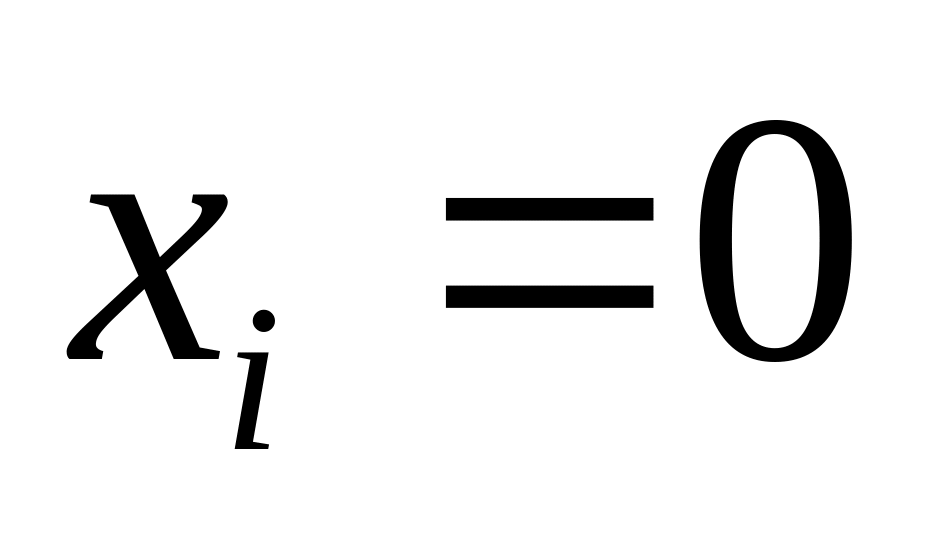то для
есть
два возможных значения – 0 и 1поэтому для каждого из указанных выше девяти векторов с количество возможных цепочек равно
, где
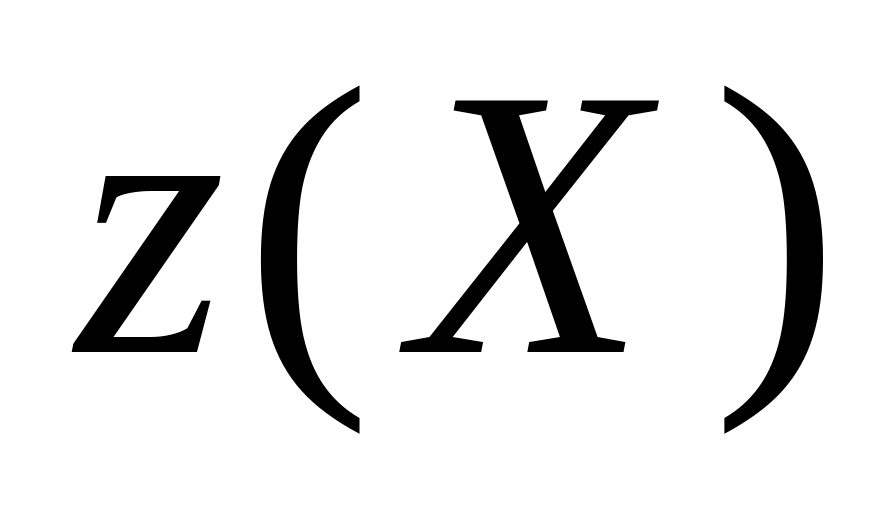–количество нулей в соответствующем
векторе
поэтому для
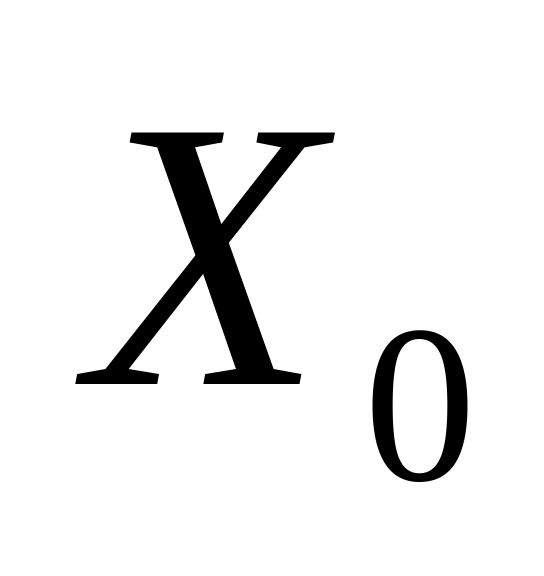(нет нулей) получаем 20 = 1 решение,
для
и
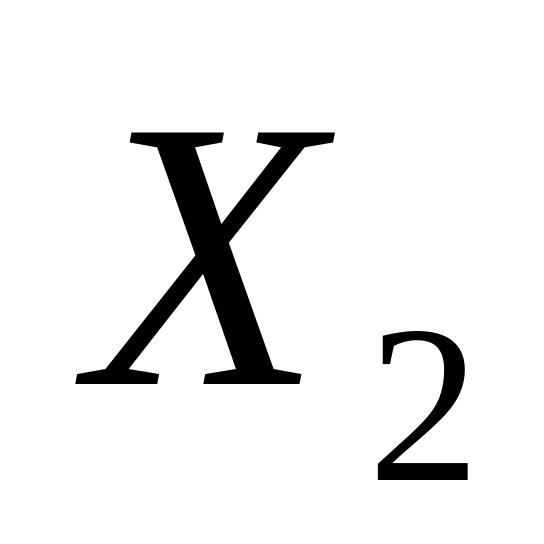(один нуль) – 21 = 2 решения; для
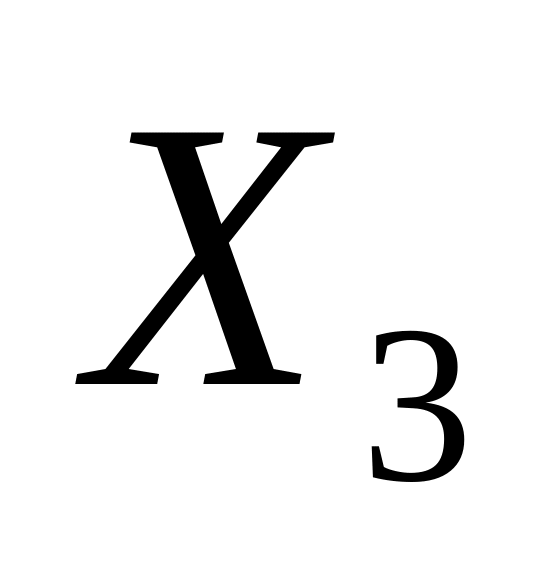и
(два нуля) – 22 = 4 решения; для
и
(три нуля) – 23 = 8 решений; для
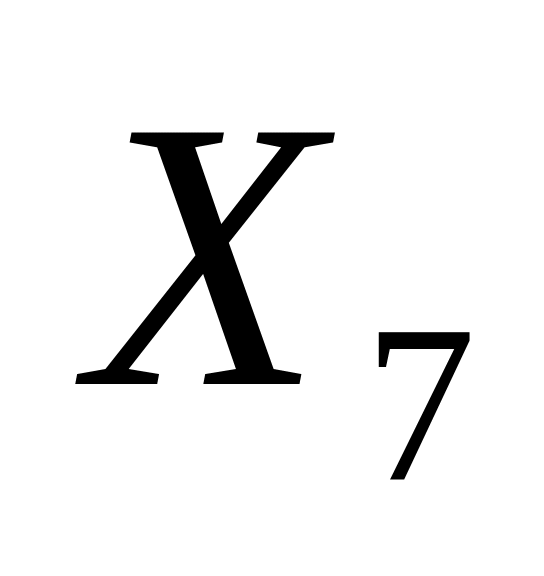и
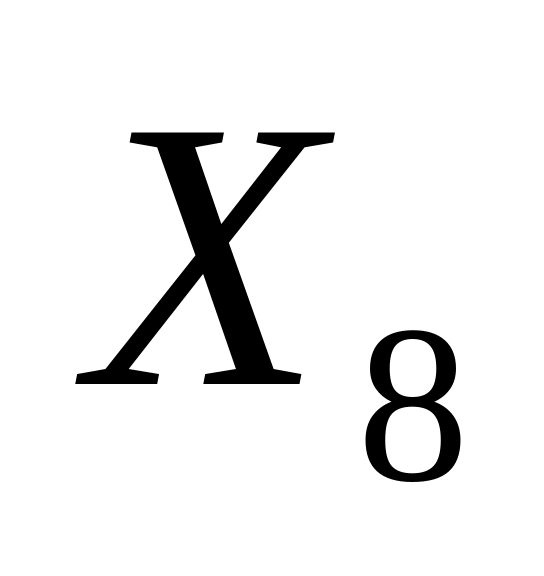(четыре нуля) – 24 = 16 решенийобщее количество решений системы 1 + 2*(21 + 22 +23 + 24) = 1 +2*30 = 61.
ответ: 61.
Ещё пример задания:
P-26. Сколько различных решений имеет система логических уравнений
(x1 x2) (x1 x2 x3) (x1 y1) = 1
(x2 x3) (x2 x3 x4) (x2 y2) = 1
(x3 x4) (x3 x4 x5) (x3 y3) = 1
(x4 x5) (x4 x5 x6) (x4 y4) = 1
(x5 x6) (x5 y5) = 1
x6 y6 = 1
где x1, …, x6, y1, …, y6, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (вариант 1, битовые цепочки, М.А. Ройтберг):
перепишем систему с более понятными обозначениями:
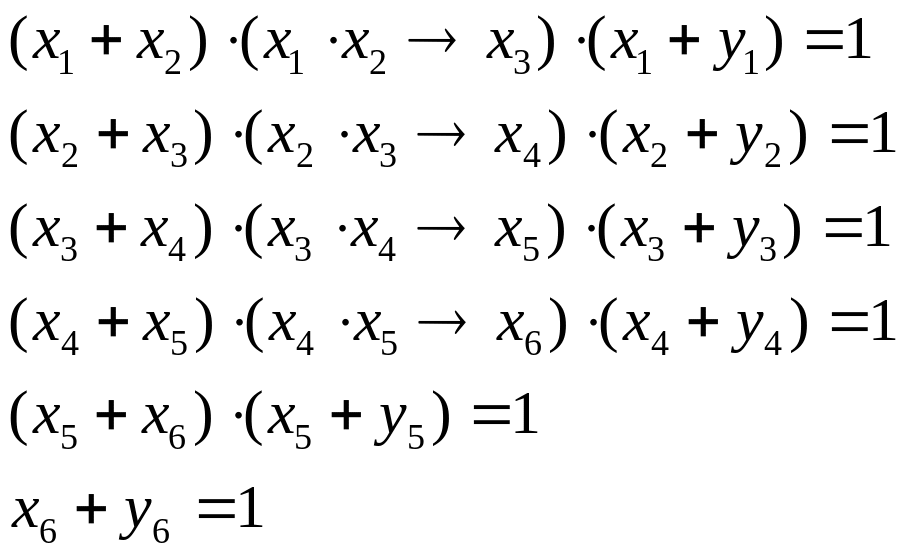
решением уравнения будут два набора логических переменных, и , которые можно представить в виде битовых цепочек:
,
первые 4 уравнения однотипны, отличаются только сдвигом номеров переменных; рассмотрим сначала их
сомножитель должен быть равен 1, поэтому в цепочке не должно быть двух идущих подряд нулей (иначе
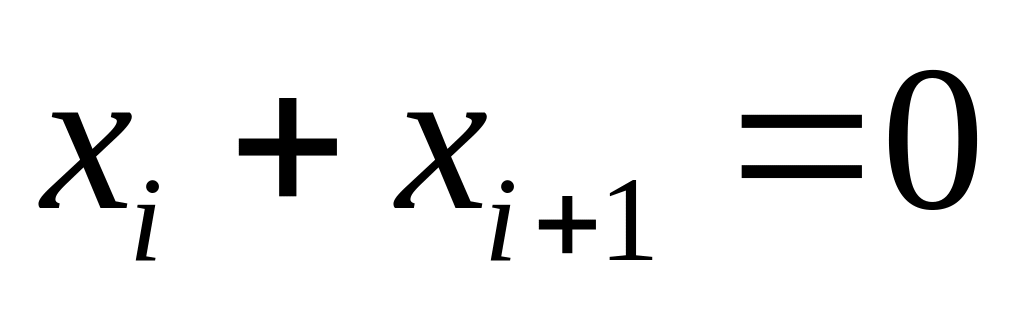и все произведение равно 0)сомножитель
должен быть равен 1, поэтому если в
цепочке
появились две единицы подряд, то дальше
идут только единицы (иначе
и все произведение равно 0)таким образом, если не учитывать (пока) сомножитель
в каждом из уравнений, существует всего
7 допустимых цепочек
,
каждая из которых определяется положением
последнего нуля (0 – вообще нет нуля):
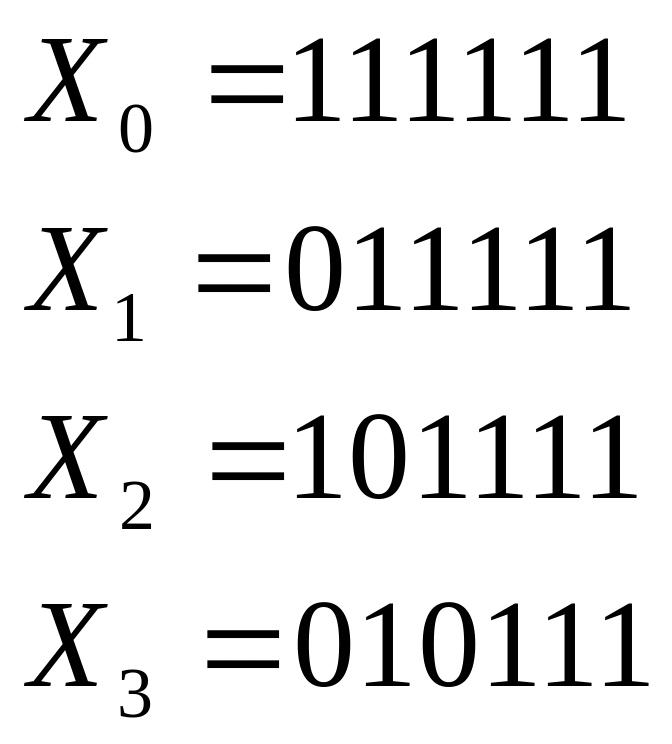
теперь рассмотрим сомножители , которые тоже должны быть равны 1; если
,
то сразу получаем
;
если же
,
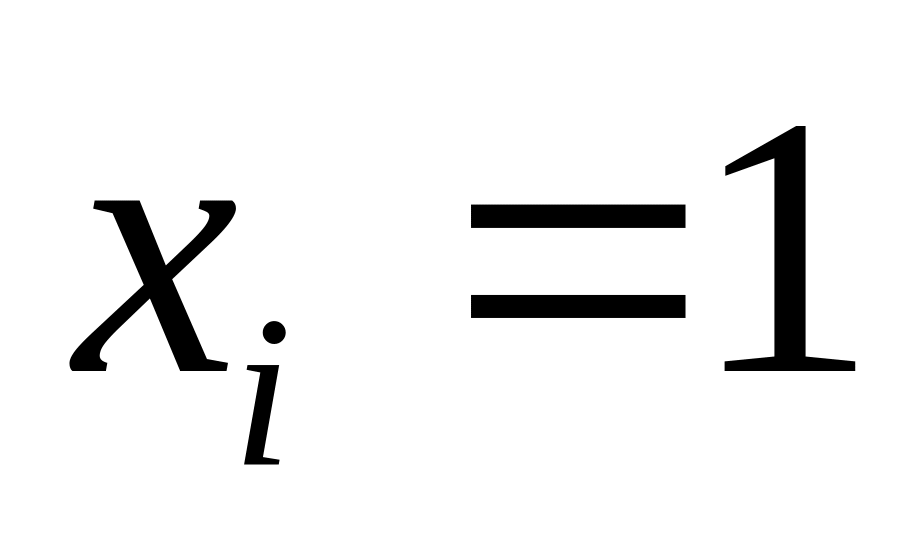то есть два варианта
таким образом, для каждой цепочки количество соответствующих цепочек равно
,
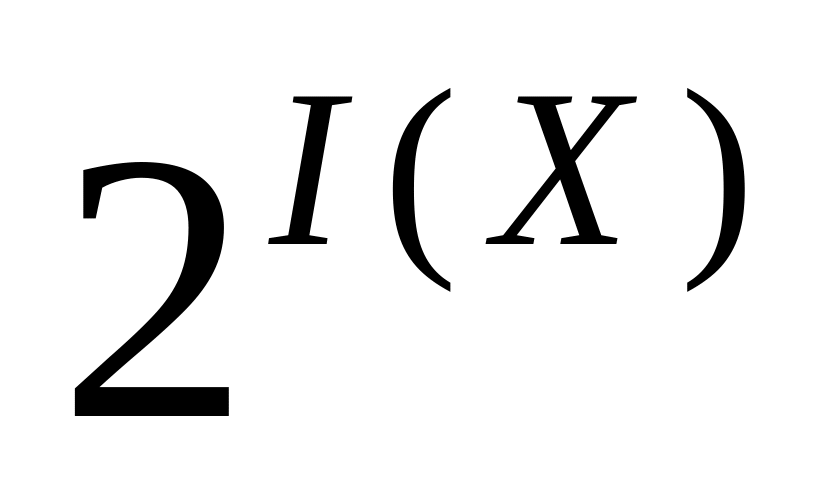где через
обозначено число единиц в цепочке
в цепочке есть 6 единиц, в цепочках и – по пять, в цепочках и – по четыре, в и – по три
поэтому общее число решений вычисляется как 26 +2∙(255555 + 24 + 23) = 64 + 2∙(325555 + 16 + 8) = 176
Ответ: 176.