
- •23 Преобразование логических выражений.
- •Пример 1:
- •Ответ: 53 Пример 2:
- •Перепишем систему уравнений в более понятном виде:
- •Будем решать задачу методом битовых цепочек;
- •Пример3 :
- •Перепишем систему уравнений в более понятном виде:
- •Будем решать задачу методом битовых цепочек;
- •Пример 4 (е.В. Хламов):
- •Перепишем систему уравнений в более понятном виде:
- •Пример 5:
- •Пример 6:
- •Ещё пример задания:
- •Ещё пример задания:
- •Ещё пример задания:
- •Ещё пример задания:
- •Ещё пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Заметим, что в третьем слагаемом тоже есть сомножитель , поэтому уравнение можно переписать в виде
- •Еще пример задания:
- •Еще пример задания:
- •Задачи для тренировки:
Пример 4 (е.В. Хламов):
P-34. Сколько различных решений имеет система логических уравнений
(x1 x2) (x2 x3) (x3 x4) = 1
(x1 y1 z1) (x1 y1 z1) (x1 y1 z1) = 1
(x2 y2 z2) (x2 y2 z2) (x2 y2 z2) = 1
...
(x4 y4 z4) (x4 y4 z4) (x4 y4 z4) = 1
где x1, …, x4, y1, …, y4, z1, …, z4, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
Перепишем систему уравнений в более понятном виде:
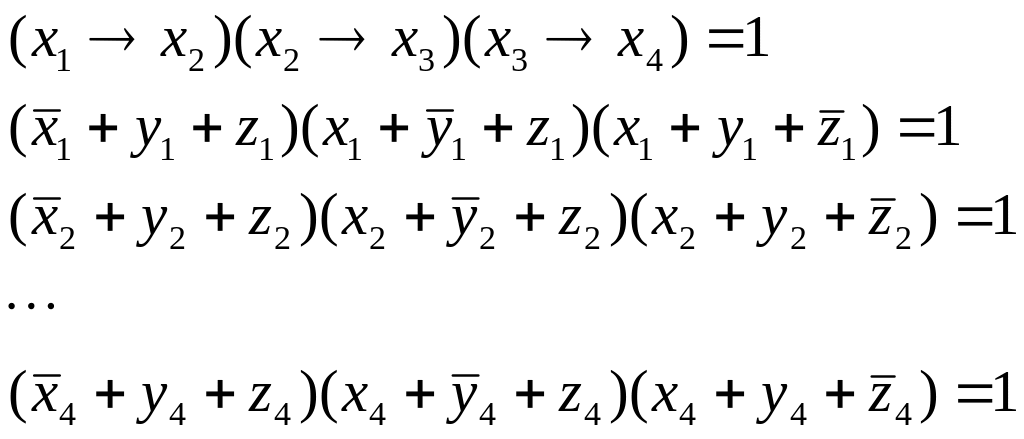
сначала решим первое уравнение, а затем посмотрим, как будет изменяться количество решений при добавлении переменных yi и zi и учёте остальных однотипных уравнений
в первом уравнении каждая скобка должна быть равна 1, поэтому в цепочке битов X = x1 x2 x3 запрещена комбинация 10; это значит, что после первой встретившейся единицы могут следовать только единицы, и любая цепочка-решение имеет структуру «все нули, потом – все единицы»
таких решений для первого уравнения – 5 штук:
0000, 0001, 0011, 0111 и 1111
теперь рассмотрим остальные уравнения, имеющие (для i=1, …, 4) одинаковую структуру
![]()
пусть в этом уравнении xi = 0, тогда получаем
![]()
этому уравнению соответствуют две
допустимых пары
![]() ,
а при двух оставшихся вариантах одна
из скобок обращается в 0
,
а при двух оставшихся вариантах одна
из скобок обращается в 0
при xi = 1 получаем
![]()
этому уравнению соответствуют три
допустимых пары
![]() ,
а при двух оставшихся вариантах одна
из скобок обращается в 0
,
а при двух оставшихся вариантах одна
из скобок обращается в 0
объединяя результаты пп. 6 и 7, получаем, что каждый нуль в решении X первого уравнения удваивает количество решений системы, а каждая единица – утраивает
таким образом первое решение X = 0000 даёт 16 = 24 решений системы, решение 0001 даёт 23 ∙ 3 = 24 решений системы, решение 0011 даёт 22 ∙ 32 = 36 решений системы, решение 0111 даёт 2 ∙ 33 = 54 решений и решение 1111 даёт 34 = 81 решений системы;
всего решений системы 16 + 24 + 36 + 54 + 81 = 211
Ответ: 211.
Пример 5:
P-32. Сколько различных решений имеет система логических уравнений
(x1 y1) (x2 y2)
(x2 y2) (x3 y3)
...
(x5 y5) (x6 y6)
где x1, …, x6, y1, …, y6, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (метод битовых цепочек):
перепишем уравнения в более понятном виде:

заметим, что по закону де Моргана
 и выполним замену переменных
и выполним замену переменных
![]()
получаем систему
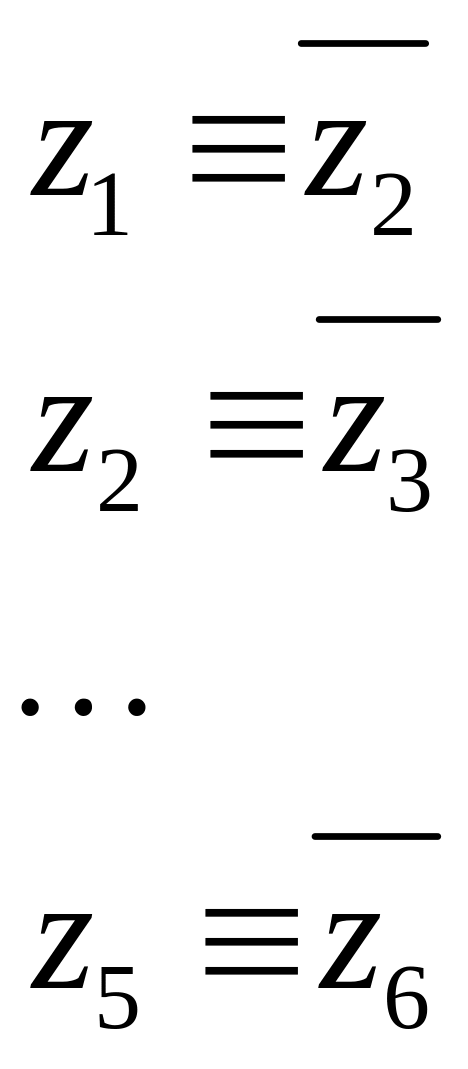
которая может быть записана в виде
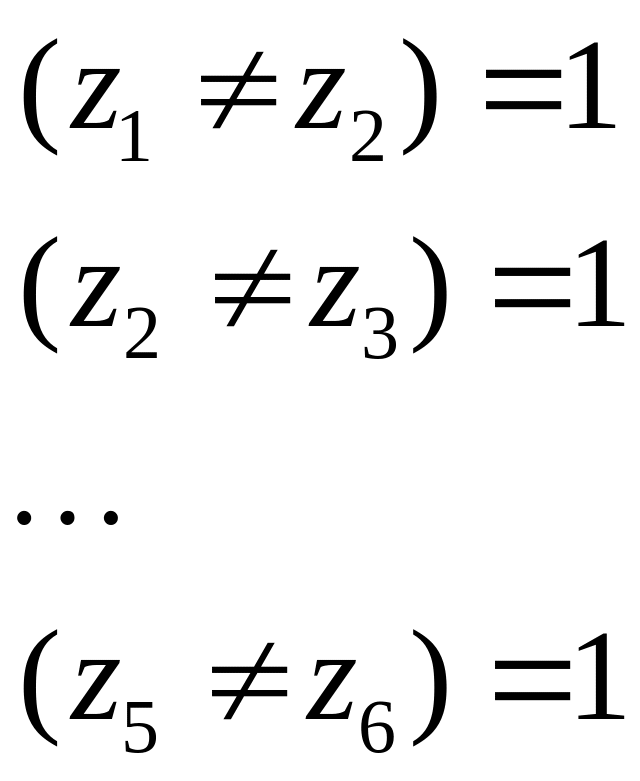
и сворачивается в одно уравнение
![]()
это уравнение накладывает такое ограничение на битовую цепочку
 :
соседние биты различны, что дает всего
дав решения:
:
соседние биты различны, что дает всего
дав решения:
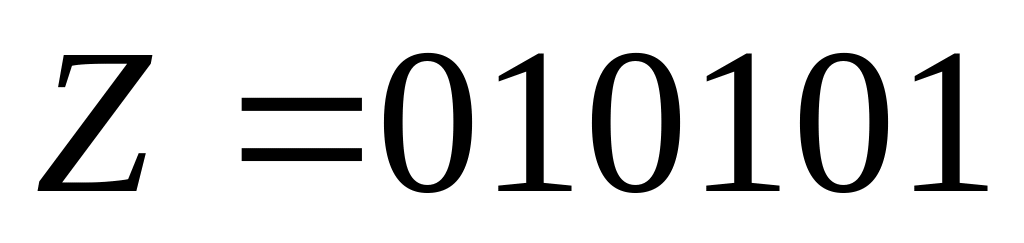 и
и

теперь нужно перейти к исходным переменным,
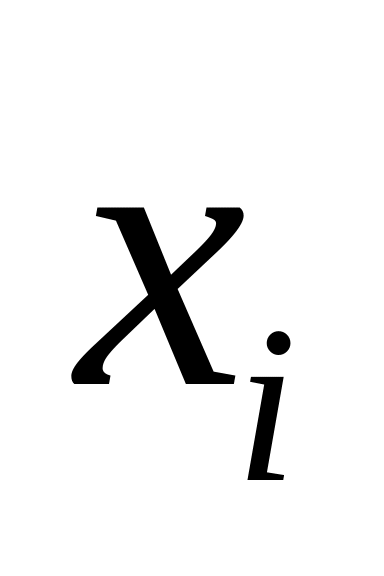 и
и

если
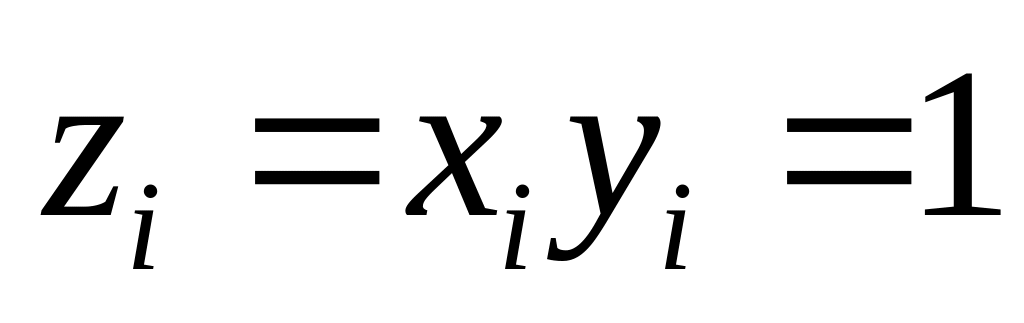 ,
то имеем всего один вариант исходных
переменных:
,
то имеем всего один вариант исходных
переменных:
 ,
то есть единица в решении Z
не увеличивает количество решений
в исходных переменных
,
то есть единица в решении Z
не увеличивает количество решений
в исходных переменныхесли
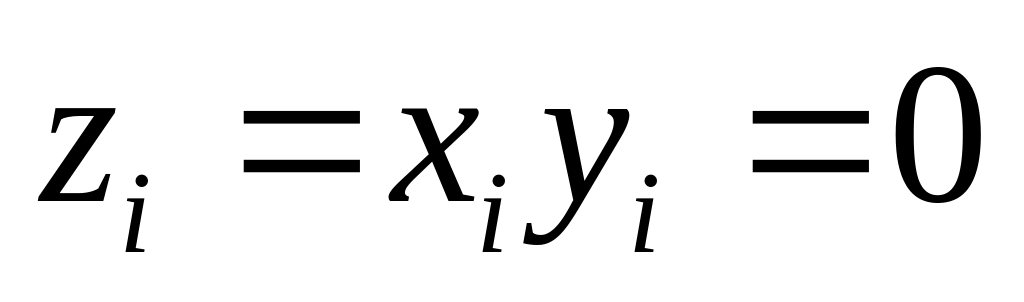 ,
то имеем три варианта исходных переменных:
,
то имеем три варианта исходных переменных:
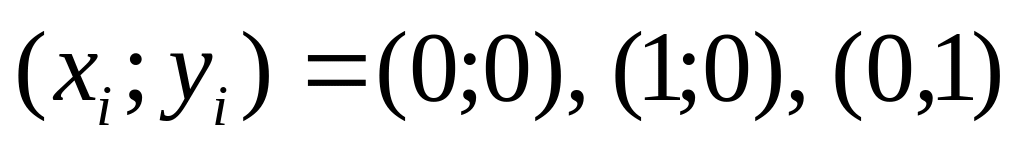 ,
то есть каждый ноль в решении Z
утраивает количество решений в
исходных переменных
,
то есть каждый ноль в решении Z
утраивает количество решений в
исходных переменныхпоскольку в каждом решении 3 нуля, каждое из двух решений Z даёт 33 = 27 решений в исходных переменных; таким образом, всего решений 2 · 27 = 54
Ответ: 54.
