23 Преобразование логических выражений.

• если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», потом – «импликация», и самая последняя – «эквиваленция»

• в приведённых задачах операция импликация считается лево-ассоциативной, то есть операции импликации в цепочке выполняются слева направо (соблюдая принцип «операции с одинаковым приоритетом выполняются слева направо»):

• правила преобразования логических выражений (законы алгебры логики):

Закон	Для И	Для ИЛИ
двойного отрицания
исключения третьего
исключения констант	A · 1 = A; A · 0 = 0	A + 0 = A; A + 1 = 1
повторения	A · A = A	A + A = A
поглощения	A · (A + B) = A	A + A · B = A
переместительный	A · B = B · A	A + B = B + A
сочетательный	A · (B · C) = (A · B) · C	A + (B + C) = (A + B) + C
распределительный	A + B · C = (A + B) · (A + C)	A · (B + C) = A · B + A · C
де Моргана

Пример 1:

Сколько различных решений имеет система логических уравнений

(x₁  (x₂  y₂))  (y₁  y₂) = 1

(x₂  (x₃  y₃))  (y₂  y₃) = 1

...

(x₇  (x₈  y₈))  (y₇  y₈) = 1

где x₁, …, x₈, y₁, …, y₈ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество наборов.

Решение:

1. перепишем систему уравнений в более понятном виде:

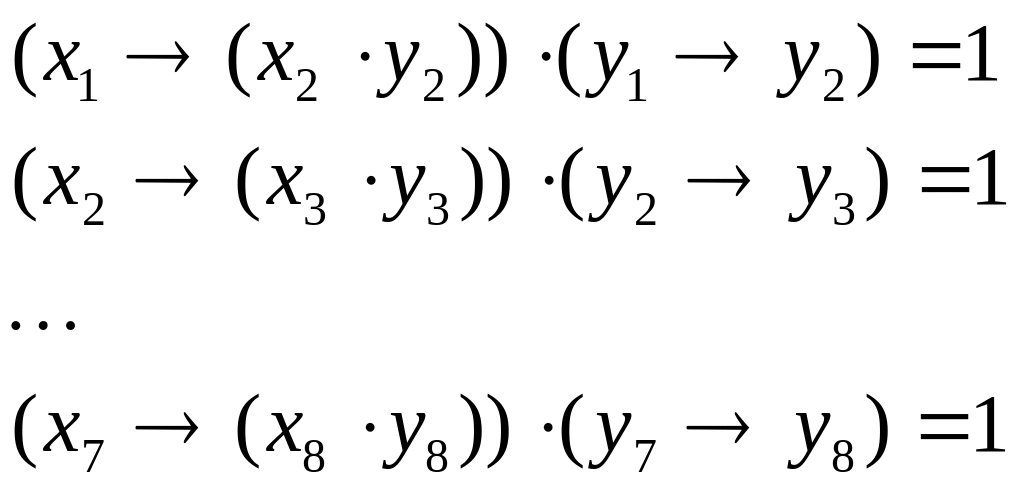
2. будем решать задачу методом битовых цепочек;

3. заметим, что первая скобка в каждом уравнении может быть переписана в виде произведения двух импликаций, например,

4. построим новую эквивалентную систему из трёх уравнений, сгруппировав сомножители «по вертикали»:

в этой системе первые два уравнения независимы, а третье представляет собой уравнение связи

5. из первого уравнение сразу следует, что в цепочке запрещена комбинация 10, то есть все допустимые цепочки X имеют структуру «все нули, потом – все единицы», их 9 штук (на 1 больше, чем число переменных):

00000000 00000001 00000011 00000111

00001111 00011111 00111111 01111111 11111111

6. те же самые решения (для цепочек ) будут и у второго уравнения, которое имеет точно такую же структуру

7. если бы третьего уравнения не было, система имела бы 81 решение (99) – каждая цепочка X может сочетаться с каждой цепочкой Y

8. остаётся учесть уравнение связи:

из которого следует, что если x_i = 1, то нужно выполнить условие y_i+1 = 1.

9. рассмотрим цепочку X = 00000000; в ней нет единиц, поэтому она сочетается со всеми Y-цепочками (9 решений)

10. рассмотрим цепочку X = 00000001; в ней одна единица, уравнение связи требует, чтобы следующий бит Y-цепочки был равен 1, но такого (9-го) бита в Y-цепочке нет поэтому эта X-цепочка сочетается со всеми Y-цепочками (9 решений)

11. рассмотрим цепочку X = 00000011; в ней две единицы, согласно уравнению связи требуется, чтобы 8-й бит Y-цепочки был равен 1, поэтому она сочетается только со всеми Y-цепочками, кроме одной – 00000000 (8 решений)

12. продолжая рассуждать тем же способом, находим, что следующие X-цепочки дают 7, 6, 5, 4, 3 и 2 решения, всего получается 2 · 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 = 53.