
1.5. Орташа мәндер туралы теоремаларға қатысты жаттығулар
1.
f(x)
= 4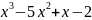 функциясына
кесіндісінде
Лагранж формуласын қолдануға бола ма?
функциясына
кесіндісінде
Лагранж формуласын қолдануға бола ма?
Шешуі.
Берілген функция
кесіндісінде үзіліссіз және әрбір x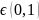 нүктесінде туындысы бар. Яғни, Лагранж
теоремасының шарттары орындалады.
нүктесінде туындысы бар. Яғни, Лагранж
теоремасының шарттары орындалады.
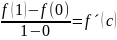 немесе f´(c)
= 0
болатындай c
нүктесін
12
немесе f´(c)
= 0
болатындай c
нүктесін
12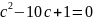 теңдеуінен табамыз: c
=
теңдеуінен табамыз: c
=
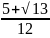 .
.
2.
Көрсетіңіздер:
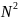 санынан артық тізбектес екі натурал
санның квадрат түбірлерінің бір-бірінен
алшақтығы
санынан артық тізбектес екі натурал
санның квадрат түбірлерінің бір-бірінен
алшақтығы
 –ден
аз болады.
–ден
аз болады.
Дәлелдеуі.
 кесіндісінде
f(x)
=
кесіндісінде
f(x)
=
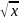 функциясына
Лагранж формуласын қолданамыз :
функциясына
Лагранж формуласын қолданамыз :
f(n+1)
– f(n) =

Егер
n
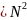 болса,
онда c
болса,
онда c
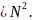 Олай
болса,
Олай
болса,
 яғни
яғни
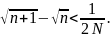
3. Дәлелдеңіздер: егер ақырлы немесе ақырсыз (a, b) интервалында f(x) функциясының шенелген f'(x) туындысы бар болса, онда f(x) функциясы (a, b) интервалында бірқалыпты үзіліссіз болады.
Дәлелдеуі.
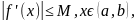 деп
алсақ, Лагранж формуласы бойынша
деп
алсақ, Лагранж формуласы бойынша
 жұбы
үшін :
жұбы
үшін :
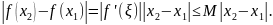
Егер
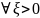 бойынша
бойынша
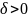 санын
санын
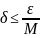 болатындай
етіп таңдасақ, онда
болатындай
етіп таңдасақ, онда
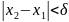 теңсіздігінен
теңсіздігінен
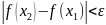 теңсіздігі
орындылытындығы , яғни функцияның (a, b)
аралығында бірқалыпты үзіліссіздігі
шығады.
теңсіздігі
орындылытындығы , яғни функцияның (a, b)
аралығында бірқалыпты үзіліссіздігі
шығады.
4.
f(x)
= 3 функциясы
функциясы
 кесіндісінде
Ферма теоремасы шарттарын қанағаттандыра
ма?
кесіндісінде
Ферма теоремасы шарттарын қанағаттандыра
ма?
Жауабы: жоқ
5. Берілген функция үшін көрсетілген аралықта Ферма теоремасы шарттары орындалатынын тексеріңіздер және f΄(c) = 0 болатын x = c мәнін табыңыздар:
a)
f(x)
= 3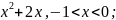
ә)
f(x)
= xlnx, 0
б)
f(x)
= -7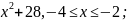
в)
f(x)
= -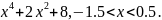
6. f(x) функциясы үшін көрсетілген аралықта Ролль теоремасының шарттары орындала ма, орындалса, f΄(c) = 0 болатын c мәні қандай?
1)
f(x)
=

Жауабы: иә, с = 1,5;
2)
f(x)
=
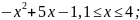
Жауабы:иә, с = 2.5;
3)
f(x)
=
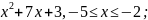
Жауабы:иә, с = 0.5;
4)
f(x)
= 4-
Жауабы: с = -3.5;
5)
f(x)
=
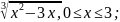
Жауабы:жоқ, у´(0) - шенелмеген;
6)
f(x)
=
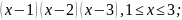
Жауабы:иә, с = 1.5;
7)
f(x)
=

Жауабы:жоқ, f’(2) жоқ;
8)
f(x)
=
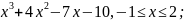
Жауабы:иә,
с
=
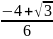 ;
;
9)
f(x) = ln sinx,
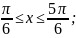
Жауабы:иә, с = ;
10)
f(x)
=

Жауабы:иә, с = ;
11)
f(x)
=
 1
1
Жауабы:иә, с = 1.5;
12)
f(x)
= 1-
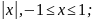
Жауабы:иә,
у´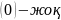 ;
;
13)
f(x)
=
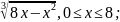
Жауабы:иә, с = 4;
14)
f(x) = tg x, 0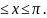
Жауабы:
жоқ, x
=
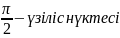 ;
;
7)
f(x)
=
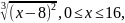 берілген.
f
(0) = f (16).
Бірақ f΄(x)
=
берілген.
f
(0) = f (16).
Бірақ f΄(x)
=
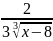 туындысы
(0, 16) интервалының ешқандай нүктесінде
0–ге тең емес. Бұл Ролль теоремасына
қайшы ма?
туындысы
(0, 16) интервалының ешқандай нүктесінде
0–ге тең емес. Бұл Ролль теоремасына
қайшы ма?
Жауабы:жоқ, өйткені теореманың шарты орындалмай тұр: f'(8) жоқ.
8) Көрсетілген аралықта берілген функция үшін Лагранж формуласын жазыңыздар:
a)
y
= sin 3x,
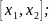
б)
y
= arc sin 2x,

ә)
y
= x (1-ln x) ,

9) Берілген функция үшін Лагранж теоремасының дұрыстығын тексеріңіздер. Дұрыс болса, Лагранж формуласындағы x = c нүктесін көрсетіңіздер:
1)
y
= 2x -
 ,
1
,
1 x
3;
x
3;
Жауабы: 2
2) y = , 0 x 1;
Жауабы: ln(e-1);
3) y = - 4x , 1 x 5;
Жауабы: 3
4)
y
=
 ,
,
 x
x
 ;
;
Жауабы: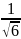 ;
;
5)
y
=
 , 0
x
3;
, 0
x
3;
Жауабы: дұрыс емес, f’(1) жоқ
6)
y
=
 ,
-2
x
2;
,
-2
x
2;
Жауабы:
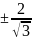 ;
;
7) y = ln x, 1 x e;
Жауабы:е-1;
8)
y
=
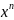 ,
0
x
a;
,
0
x
a;
Жауабы: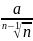 ;
;
9)
y
=
 , -
, -
 x
.
x
.
Жауабы: жоқ, y’(0) жоқ;
10) Лагранж формуласын қолданып, теңсіздікті дәлелдеңіздер :
1)
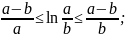
2)
 1
;
1
;
3)
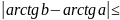 b – a ;
b – a ;
4)

5)
 ;
;
6)
n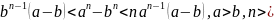 1;
1;
7)
n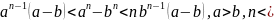 1;
1;
8)
 0
.
0
.
11)
кесіндісінде
(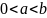 )
берілген
f(x)
және
функциялары
үшін Кoши
формуласын жазыңыздар:
)
берілген
f(x)
және
функциялары
үшін Кoши
формуласын жазыңыздар:
1)
f(x)
= sinx,
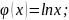
2)
f
(x) =
 .
.
12) Берілген функциялар үшін Коши теоремасының дұрыстығын тексеріңіздер және x = c нүктесін табыңыздар:
1)
f(x)
=
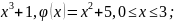
Жауабы: с = 2;
2)
f(x)
= -
Жауабы:
с
=
 ;
;
3)
f(x)
= 2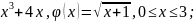
Жауабы:
с
=(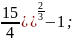
4)
f(x)
= cosx,

Жауабы:
с
=
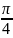 ;
;
5)
f(x)
=
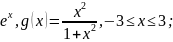
Жауабы: жоқ, g(-3)=g(3);
6)
f(x)
=
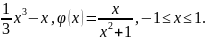
Жауабы:
с
= ;
;
13) f(x) = (x-1)(x-2)(x-3) функцияға Ролль теоремасы орындала ма?
Жауабы:
берілген f(x)
функциясы
 сегментте
дифференциалданады және сегменттің
x=1,
x=2,
x=3
нүктелерінде
нөлге айналады. Олай болса, f(x)
функцияға
сегментте
дифференциалданады және сегменттің
x=1,
x=2,
x=3
нүктелерінде
нөлге айналады. Олай болса, f(x)
функцияға
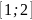 және
және
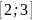 сегменттерде
Ролль теоремасының барлық шарттары
орындалады. f(x)
функция
үшінші дәрежелі көпмүшелік болғандықтан,
(1;3)
интервалдан f’(x)=0
теңдікті
қанағаттандыратын екі нүкте табылады.
Функцияны дифференциалдап және оны
нөлге теңестіріп, квадрат теңдеу
аламыз:3
сегменттерде
Ролль теоремасының барлық шарттары
орындалады. f(x)
функция
үшінші дәрежелі көпмүшелік болғандықтан,
(1;3)
интервалдан f’(x)=0
теңдікті
қанағаттандыратын екі нүкте табылады.
Функцияны дифференциалдап және оны
нөлге теңестіріп, квадрат теңдеу
аламыз:3 Сонымен жоғарыда айтылған екі нүктені
табамыз:
Сонымен жоғарыда айтылған екі нүктені
табамыз:

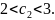
14)
f(x)=1-
функция
x=-1,
x=1 нүктелерде
нөлге айналады, бірақта f’(x)
барлық
x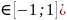 Ролль
теоремасын қараңыз).
Ролль теоремасына келетін қайшылықты
түсіндір.
Ролль
теоремасын қараңыз).
Ролль теоремасына келетін қайшылықты
түсіндір.
Жауабы:
Ролль теоремасының 2)-шарты орындалмайды:
f(x)
функцияның
x=0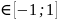 нүктеде
туындысы жоқ. Шынында да
нүктеде
туындысы жоқ. Шынында да
f’(-0)= f’(+0)=
f’(+0)=
15)
Барлық x,
y үшін
 теңсіздігінің
орындалатынын дәлелдейік.
теңсіздігінің
орындалатынын дәлелдейік.
Жауабы:
Oл
үшін Лагранж формуласын пайдаланамыз.
Косинус x
функциясы
 сегментте
Лагранж теоремасының барлық шарттарын
қанағаттандырады, сондықтан
сегментте
Лагранж теоремасының барлық шарттарын
қанағаттандырады, сондықтан
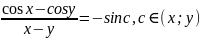 .
Осыдан
.
Осыдан
 Онда
Онда
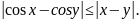
16)
f(x)=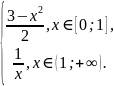
функциясының
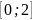 сегменттегі
c
аралық
мәнін Лагранж формуласын пайдаланып
табайық.
сегменттегі
c
аралық
мәнін Лагранж формуласын пайдаланып
табайық.
Жауабы: Функция x=1 нүктеде дифференциалданатынын тексерейік. Функцияның біржақты шектерінің анықтамасы бойынша :
f’(1-0)=
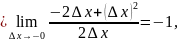
f’(1+0)=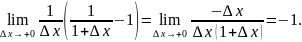
Демек f(x) функция x=1 нүктеде дифференциалданады. Енді Лагранждың формуласын сегментте f(x) функцияға пайдаланайық:
f(2)-f(0)=2.
f’(c), c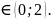
Сонда,
f(2)= ал
f(0)=
ал
f(0)= болғандықтан
және
болғандықтан
және
f’(x)=
онда
-1=
Осыдан
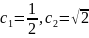 болады.
болады.
17)
f(x)= функция
үшін берілген жиында
Ролль
теоремасының шарттары орындалатынын
тексеріңіз және орындалған жағдайда
f’(c)=0
болатын
x=c
нүктелерін
табыңыз.
функция
үшін берілген жиында
Ролль
теоремасының шарттары орындалатынын
тексеріңіз және орындалған жағдайда
f’(c)=0
болатын
x=c
нүктелерін
табыңыз.
Жауабы: f(x) функциясы берілген жиында үзіліссіз, (1;2) аралықта ақырлы туындыға ие және f(1)=f(2)=0. Сондықтан бұл функцияға Ролль теоремасын қолдануға болады. f’(x)=-2x+3=0 шарттан c=1.5 екендігі шығады.
18) Көрсетілген кесіндіде анықталған функция үшін Лагранж теоремасының дұрыстығын тексеріп, f(b)-f(a)=f’(c)(b-a) формуладағы нүктелерін анықтаңыз.
f(x)=2x-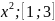
Шешуі. Берілген функция кесіндіде үзіліссіз, (1;3) аралықта f’(x)=2-2x ақырлы туындысы бар, яғни дифференциалданады. Демек, Лагранж теоремасын қолдануға болады. f(1)=1, f(3)=-3, b-a=3-1=2 және f’(c)=2-2c екендігін ескерсек, f(b)-f(a)=f’(c)(b-a) формула бойынша -3-1=f’(c) немесе -4=(2-2c) 2 болады. Бұдан c=2.
19)
f(x)
және
g(x)
функциялары
үшін берілген кесіндіде Коши теоремасының
дұрыстығын тексеріп, Коши формуласындағы
x=c
нүктесін
(бар
болса )
табыңыз:
f(x)=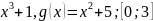 .
.
Шешуі.
Берілген функциялар
 кесіндісінде
үзіліссіз, (0;3) аралығында дифференциалданады.
f’(x)=3
кесіндісінде
үзіліссіз, (0;3) аралығында дифференциалданады.
f’(x)=3 әрі
(0;3) аралығында 2x
әрі
(0;3) аралығында 2x Демек, Коши теоремасының барлық шарттары
орындалады. f(0)=1,
f(3)=28, g(0)=5, g(3)=14 және
g’(c)=2,
f’(c)=3
Демек, Коши теоремасының барлық шарттары
орындалады. f(0)=1,
f(3)=28, g(0)=5, g(3)=14 және
g’(c)=2,
f’(c)=3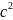 екендігін
ескеріп, Коши формуласына қойсақ:
екендігін
ескеріп, Коши формуласына қойсақ:
 немесе
3=
немесе
3=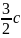 болады.
Бұдан
c=2.
болады.
Бұдан
c=2.
20)
f(x)=arctg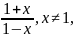 және
f(1)=0
функцияның
шектеулі
және
f(1)=0
функцияның
шектеулі
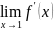 шегі
бар болатынын, ал бірақ функцияның
шектеулі
шегі
бар болатынын, ал бірақ функцияның
шектеулі
f’(1-0), f’(1+0) біржақты шектері жоқ болатынын дәлелдейік.
Дәлелдеуі:
Ол үшін Лагранж формуласын кез келген
 сегментте
жазайық:
сегментте
жазайық:
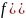
Осы
теңдіктен
 –да
шекке көшейік:
–да
шекке көшейік:
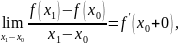
ал анықтама бойынша
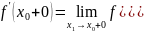
Енді
x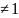 болсын,
онда
болсын,
онда
f’(x)=
ал функцияның біржақты шектерінің анықтамасы бойынша x=1 нүктеде :
f‘(1+0)=
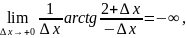
f’(1-0)=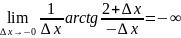 .
.
