
- •Тема 6. Дерева. 96
- •Тема 1 Множини. Операції над множинами
- •1. Основи теорії множин
- •2. Види множин
- •3. Операції над множинами
- •4. Розбиття і покриття.
- •5. Властивості операцій над множинами:
- •6. Ком’ютерне зображення множин
- •Тема 2 Комбінаторика
- •1. Класичні задачі комбінаторики
- •2. Правило суми та добутку
- •3. Основні формули
- •4. Задача про цілочислові розв'язки
- •5. Біном н’ютона
- •6. Арифметичний трикутник (трикутник Паскаля)
- •7. Розв’язування рекурентних рівнянь.
- •8. Числа Фібоначчі
- •Тема 3. Основи теорії відношень
- •1. Основні поняття теорії відношень
- •2. Способи задання бінарних відношень
- •3. Операції над відношеннями
- •4. Властивості бінарних відношень
- •1. Рефлексивність
- •2. Антирефлексивність
- •3. Симетричність
- •4. Несиметричність
- •5. Антисиметричність
- •6. Транзитивність
- •7. Антитранзитивність
- •5. Відношення еквівалентності, порядку, толерантності
- •Тема 4. Теорія функцій. Алгебри
- •1. Алгебраїчні структури
- •2. Алгебри булевих функцій
- •Тема 5. Теорія графів
- •1. Основні означення та властивості
- •2. Деякі спеціальні класи простих графів
- •3. Способи подання графів
- •3.1. Матриця інцидентності
- •3.2. Матриця суміжності
- •3.3. Подання графа списком пар (списком ребер)
- •3.4. Подання графа списками суміжності
- •3.5. Матриці досяжностей і контрдосяжностей
- •4. Шляхи та цикли. Зв’язність
- •4.1. Головні означення та результати. Термінологія
- •4.2. Характеристики зв’язності простого графа
- •5. Ізоморфізм графів
- •6. Ейлерів цикл у графів
- •7. Гамільтонів цикл у графі
- •8. Зважені графи та алгоритми пошуку найкоротших шляхів
- •9. Обхід графів
- •9.1. Пошук углиб у простому зв'язному графі
- •9.2. Пошук ушир у простому зв'язному графі
- •10. Планарні графи
- •11. Розфарбування графів
- •12. Незалежні множини вершин. Кліки
- •Тема 6. Дерева.
- •1. Основні означення та властивості
- •2. Рекурсія. Обхід дерев. Префіксна та постфіксна форми запису виразів
- •43018, Луцьк-18, вул. Львівська,75
Тема 3. Основи теорії відношень
1. Основні поняття теорії відношень
2. Способи задання бінарних відношень
3. Операції над відношеннями
4. Властивості бінарних відношень
5. Відношення еквівалентності, порядку, толерантності
1. Основні поняття теорії відношень
Відношення – одне з основних понять сучасної математики. Мову відношень використовують для опису зв'язків між об'єктами та поняттями. Найзручніший спосіб задати зв'язок між елементами двох множин - записати впорядковані пари елементів, що перебувають у цьому зв'язку.
Відношення реалізують у математичних термінах на абстрактних множинах реальні зв'язки між реальними об'єктами. Відношення застосовуються при побудові комп'ютерних баз даних, які організовані у вигляді таблиць даних. Зв'язки між групами даних у таблицях описуються мовою відношень. Самі дані обробляються і перетворюються за допомогою операцій, математично точно визначених для відношень. Такі бази даних називаються реляційними і широко застосовуються для збереження та обробки найрізноманітнішої інформації: виробничої, комерційної, статистичної тощо. Відношення також часто використовуються в програмуванні. Такі складові структури даних, як списки, дерева тощо звичайно використовуються для опису деякої множини даних разом з відношенням між елементами цієї множини.
Декартовим
добутком множин А та В
(позначають
![]() )
називають множину всіх пар (а,b),
таких, що
)
називають множину всіх пар (а,b),
таких, що
![]() .
Зокрема, якщо А=В, то обидві компоненти
належать до А. Такий добуток позначають
через А2
і називають декартовим
квадратом множини А.
Аналогічно, декартовим добутком множин
.
Зокрема, якщо А=В, то обидві компоненти
належать до А. Такий добуток позначають
через А2
і називають декартовим
квадратом множини А.
Аналогічно, декартовим добутком множин
![]() (позначають
(позначають
![]() )
називають множину всіх впорядкованих
наборів (кортежів)
)
називають множину всіх впорядкованих
наборів (кортежів)
![]() довжини п
таких, що
довжини п
таких, що
![]() .
Частковий випадок
.
Частковий випадок
![]() позначають
позначають
![]() і називають п-м
степенем множини Х.
і називають п-м
степенем множини Х.
Прпиклад.
Нехай
![]() ,
,
![]() ,
,![]() .
.
Тоді
![]()
![]()
![]()
п- арне
відношення R на
множинах
- це
підмножина декартового добутку цих п
множин:
![]() .
.
Якщо
набір елементів
![]() належить відношенню
R,
то стверджують, що елементи
знаходяться у відношенні
R.
належить відношенню
R,
то стверджують, що елементи
знаходяться у відношенні
R.
Під
п- арним відношенням
R
на множині X
розуміється підмножина
п-го степеня
цієї множини:
![]() .
.
Якщо
п =
1, то відношення називається унарним,
якщо п
= 2 -бінарним. Зауважимо,
що унарне відношення R
на множині X
- це підмножина в
самому X
:
![]() .
.
Приклад.
Відношенням на множинах
А, В, С з
попереднього прикладу є будь-яка
підмножина множини
![]() ,
зокрема
,
зокрема
![]() ,
,
![]()
Розглянемо окремо бінарні відношення, які є "базисними" у тому розумінні, що будь-яке п-арне відношення можна зобразити у вигляді ланцюжка бінарних відношень, що послідовно конструюються. Цей очевидний факт є наслідком асоціативності декартового добутку множин.
2. Способи задання бінарних відношень
Якщо
R
- бінарне відношення
на множинах Х,У, то
факт
![]() часто записується у
вигляді
часто записується у
вигляді
![]() . і говорять, що елемент
. і говорять, що елемент
![]() знаходиться у відношенні
R
з елементом
знаходиться у відношенні
R
з елементом
![]() .
.
Будь-яке бінарне відношення може бути задане у вигляді списку, елементами якого є пари, з яких складається відношення.
На
множинах чисел А =
{1,2,3,4,5,6,7,8,9}; В
= {24,25,26} побудуємо
відношення "дільник", яке складається
з упорядкованих пар виду
![]() ,
де x
– дільник y,
,
де x
– дільник y,
![]() ,
,
![]() .
.
Приклад. Позначимо це відношення через R :
![]() .
.
Бінарне відношення R на множинах X і У може бути задане за допомогою матриці
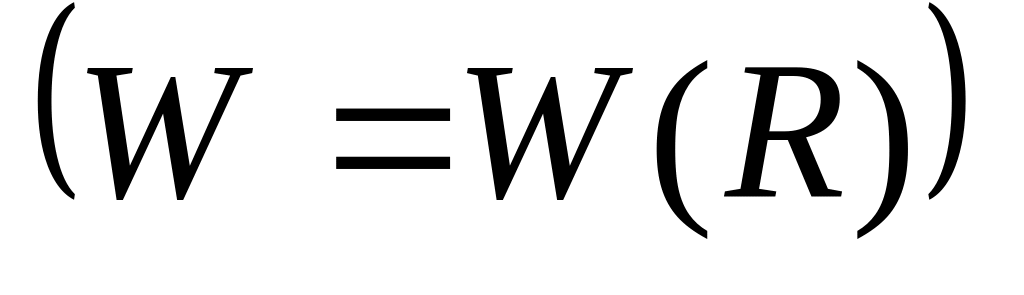 ,
рядки якої відповідають елементам
множини X, стовпці - елементам множини
У. Якщо
,
рядки якої відповідають елементам
множини X, стовпці - елементам множини
У. Якщо
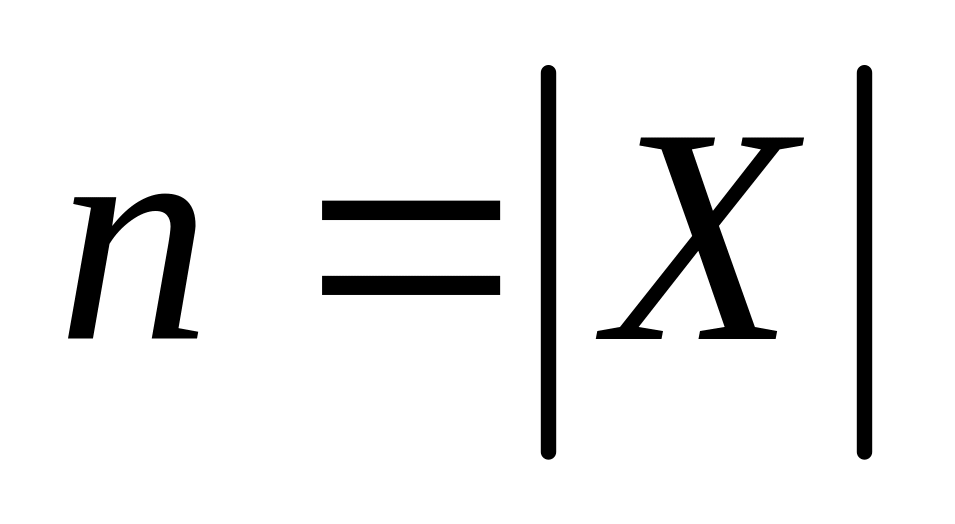 ,
,
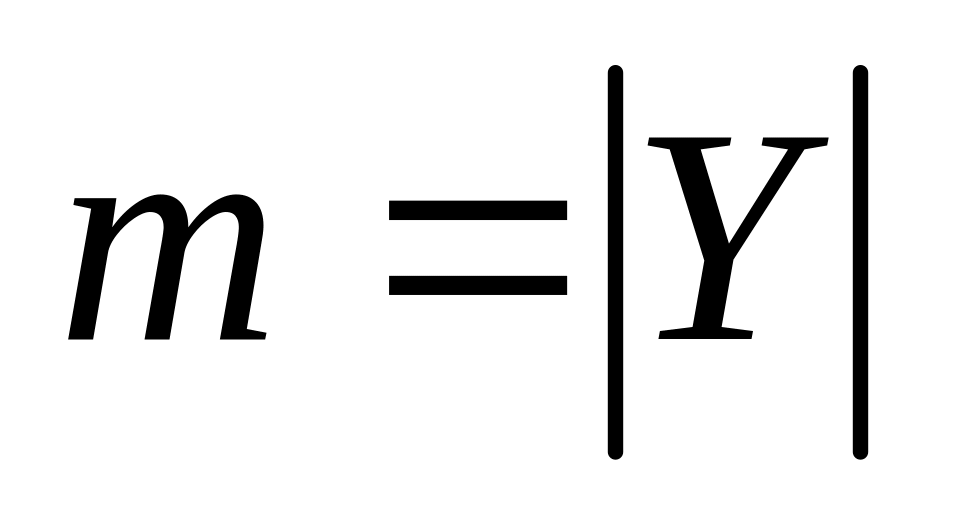 – кількість елементів множин X і Y
відповідно, то довільна матриця W
має розмір
– кількість елементів множин X і Y
відповідно, то довільна матриця W
має розмір
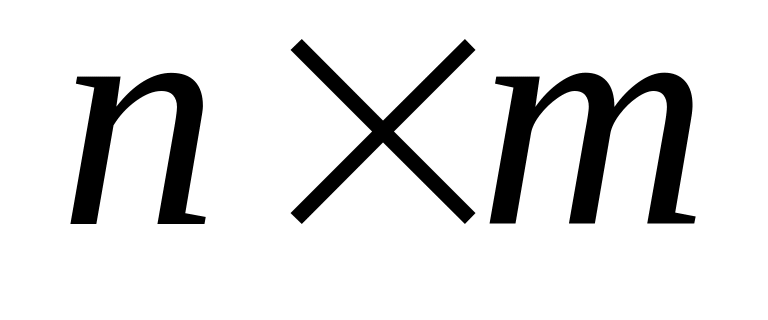 .
Елемент
.
Елемент
 матриці відповідає парі
матриці відповідає парі
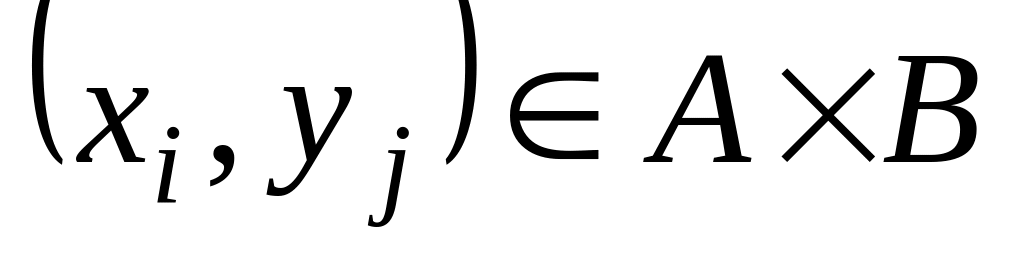 декартового добутку множин, причому
декартового добутку множин, причому
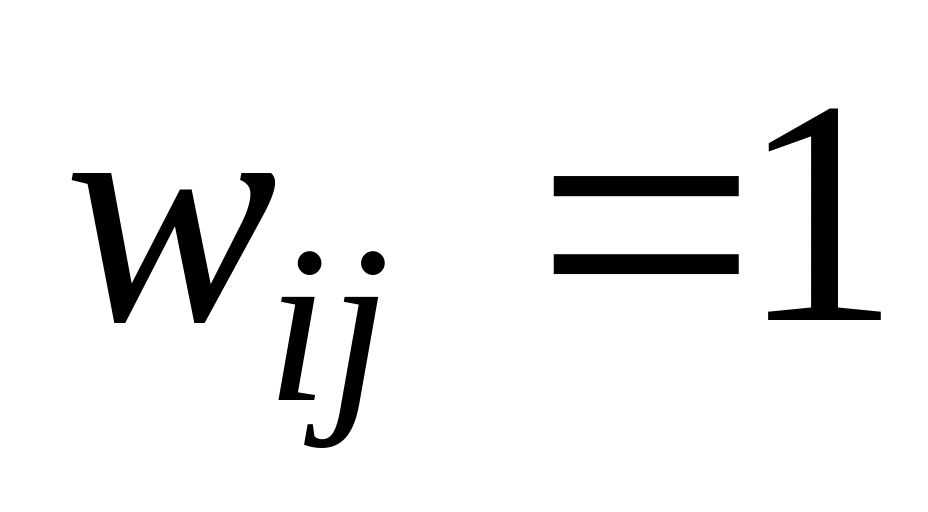 ,
якщо
,
якщо
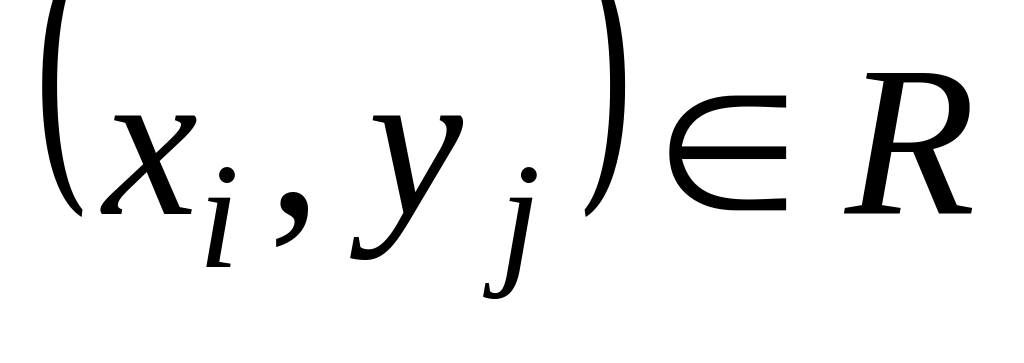 ,
і
,
і
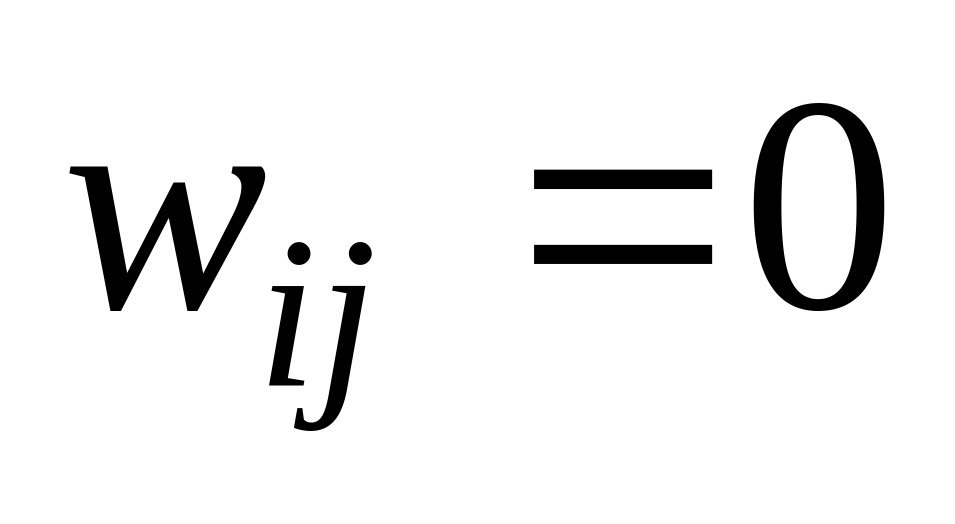 ,
якщо
,
якщо
 ,
тобто відношення R
не містить пару
,
тобто відношення R
не містить пару
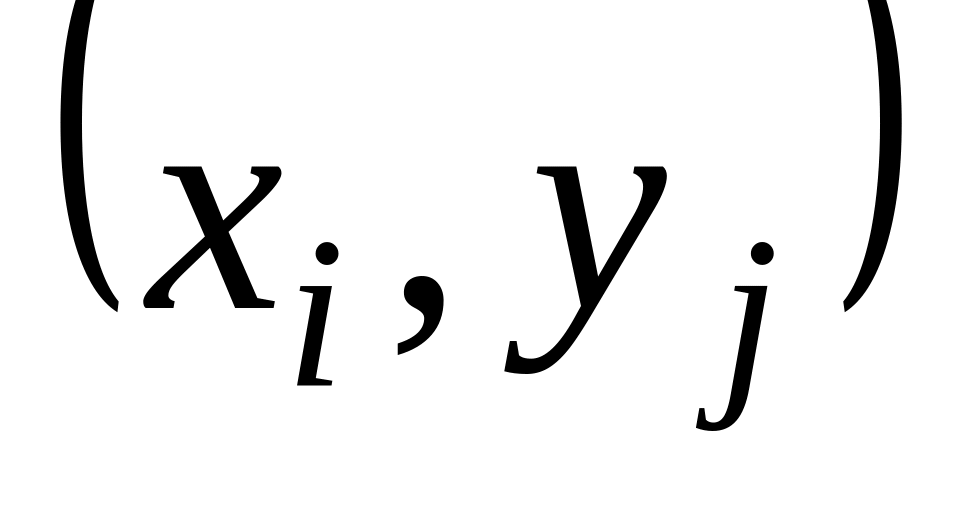 .
.
Приклад. Наступна матриця W задає відношення R "дільник" для числових множин А і В з попереднього прикладу:

Бінарне відношення R на множинах X, Y може бути задане графічно.
На
площині зобразимо точками
![]() елементи множин X
і Y.
Якщо пара
елементи множин X
і Y.
Якщо пара
![]() належить відношенню R,
з'єднаємо точки х
,у
лінією, яка спрямована від першого
елемента пари до другого. Позначивши
таким чином всі пари, що належать
відношенню R,
одержимо фігуру, яка називається графом
відношення. Спрямовані лінії, що з'єднують
пари точок називаються дугами,
а точки, що зображують елементи множин
- вершинами
графа. Якщо бінарне відношення R
задане на одній множині
належить відношенню R,
з'єднаємо точки х
,у
лінією, яка спрямована від першого
елемента пари до другого. Позначивши
таким чином всі пари, що належать
відношенню R,
одержимо фігуру, яка називається графом
відношення. Спрямовані лінії, що з'єднують
пари точок називаються дугами,
а точки, що зображують елементи множин
- вершинами
графа. Якщо бінарне відношення R
задане на одній множині
![]() то вершинами графа
будуть елементи множини X
.
то вершинами графа
будуть елементи множини X
.
Бінарні відношення можна задавати графічно за допомогою діаграм Хассе.

Граф відношення «батько»
Відношення ''батько" в даному випадку задане на множині, що складається з 9 осіб. Упорядковані пари елементів множини, що належать відношенню, з'єднанні дугами графа. Перший елемент такої групи с батьком, другий - його дитиною. Дуга графа спрямована від першого елемента до другого.
Розглянемо
деякі часткові випадки відношень. Нехай
задане бінарне відношення R
на множині
![]() .
Можливий випадок,
коли
.
Можливий випадок,
коли
![]() – таке відношення називається повним.
Для п'ятиелементної
множини А граф
повного відношення зображено на рис.
2,б. Може трапитися, що
– таке відношення називається повним.
Для п'ятиелементної
множини А граф
повного відношення зображено на рис.
2,б. Може трапитися, що
![]() , –
таке відношення називається порожнім.
При
, –
таке відношення називається порожнім.
При
![]() граф зображено на рис. 2,в. Якщо відношення
містить всі можливі пари виду (а,а)
і не містить інших
пар елементів, то таке відношення
називається тотожним.
Граф цього відношення
зображено на рис. 2,а
для
.
граф зображено на рис. 2,в. Якщо відношення
містить всі можливі пари виду (а,а)
і не містить інших
пар елементів, то таке відношення
називається тотожним.
Граф цього відношення
зображено на рис. 2,а
для
.

а) б) в)
Рис.2. Граф підношення: а) тотожного: б) повного: в)порожнього.
Якщо повне відношення задане за допомогою матриці, то всі елементи цієї матриці дорівнюють одиниці. Матриця порожнього відношення складається з нульових елементів.
Ми
вивчили три способи задання відношень.
Переліченням елементів можливо задавати
n-арні
відношення при
![]() .
За допомогою матриці
і графа зручно задавати тільки бінарні
відношення.
.
За допомогою матриці
і графа зручно задавати тільки бінарні
відношення.
