4. Задача про цілочислові розв'язки

Цю задачу формулюють так: знайти кількість розв'язків рівняння у цілих невід'ємних числах, де п – ціле невід'ємне число.

Узявши такі невід'ємні цілі числа що можна одержати сполучення з повтореннями з r елементів по п, а саме: елементів першого типу – х1 одиниць, другого – х2, ..., r-го – х_r. Навпаки, якщо є сполучення з повтореннями з r елементів по п, то кількість елементів кожного типу задовольняють вимоги рівняння у цілих невід'ємних числах. Отже, кількість цілих невід'ємних розв'язків цього рівняння дорівнює:

Приклад. Знайдемо кількість невід'ємних цілих розв'язків рівняння х1+х2+х3=10. Безпосереднє використання попередньої формули дає

Кількість розв'язків рівняння x1+х2+...+хr = п у цілих невід'ємних числах можна визначити й тоді, коли на змінні накладено певні обмеження.

Приклад. Знайдемо кількість невід'ємних цілих розв'язків рівняння

де

Зробимо заміну змінних:

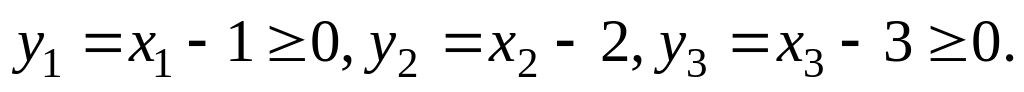
Отримаємо рівняння:

отже, кількість цілочисельних розв’язків:

Приклад. Визначимо кількість розв'язків нерівності в невід'ємних цілих числах. Уведемо допоміжну змінну х4, яка може набувати цілих невід'ємних значень, і перейдемо до еквівалентної задачі: визначити кількість розв'язків рівняння х₁+х₂+х₃+х₄ = 10 в невід'ємних цілих числах. Отже,

Перестановки з повтореннями. Розглянемо задачу: Маємо предмети r різних видів. Скільки різних комбінацій (перестановок) можна зробити з предметів 1-го виду, з предметів 2-го виду, …, з предметів r-го виду? Число предметів в кожній перестановці . Такі комбінації називаються перестановками з повтореннями. Їх число позначається і обчислюється за формулою:

.

Приклад. Скількома способами можна розмістити в ряд 5 чорних, 4 білих і 3 червоних фішки?

Розв’язок. Ця задача на перестановки з повтореннями. Маємо фішки 3 різних видів: чорних , білих , червоних . Всього фішок 12. Отже за формулою маємо способів.

Зауваження. Якщо , , то маємо .

5. Біном н’ютона

Числа виникають як коефіцієнти при розкритті дужок в біномі .

Наприклад

Кожен з 8 доданків в 2-му рядочку перетворень отримали при перемноженні 3-х змінних, які вибираємо по одному з кожної дужки. Видно, що рівно 3 доданки містять одну змінну a і дві b. Це відбувається тому що у нас є способи вибору двох дужок із трьох, звідки ми беремо змінну b, а з тої що залишилася вибираємо a.

В загальному випадку, розкриваючи дужки в біномі , ми будемо отримувати члени виду ( де r набуває кожне із значень від 0 до п при перемноженні символів b, взятих з r дужок, і a , взятих із (n-r) тих дужок, що залишилися. Так як є рівно способів r дужок з n, то в нас буде в точності членів виду при . Звідси

.

або .

Ця формула називається біномом Н’ютона. Тому коефіцієнти називають біноміальними коефіцієнтами.

Тепер узагальним біноміальну теорему для випадку знаходження коефіцієнтів розкладу .

Теорема. Для заданого додатного числа п

, де сума взята по всім невід’ємним цілим числам , таким що .

Приклад. Знайдемо коефіцієнт при в розкладі .

Розв’язок. Цей коефіцієнт рівний .