3.5. Матриці досяжностей і контрдосяжностей

Матриця досяжностей визначаються наступним чином:

Множини вершин графа G, досяжних із заданої вершини , складається з таких елементів , для яких -й елемент в матриці досяжностей рівний 1. Очевидно що всі діагональні елементи в матриці R рівні 1, оскільки кожна вершина досяжна із себе самої з допомогою шляху довжиною 0.

Оскільки Г являється множиною таких вершин , які досяжні із з використанням шляхів довжиною 1 (тобто Г – така множина вершин, для яких в графі існують дуги ) і оскільки Г являється множиною вершин, досяжних із з допомогою шляхів довжиною 1, то множина Г(Г )= складається із вершин досяжних із з використанням шляхів довжиною 2. Аналогічно являється множиною вершин, які досяжні і з допомогою шляхів довжиною p.

Так як будь-яка вершина графа G, яка досяжна із , повинна бути досяжна з використанням шляху (або шляхів) довжиною 0, або 1, або 2,…, або p (з деякими кінцевими, але, можливо достатньо більшим значенням p), то множина вершин, досяжних із , можна представити в вигляді

(1)

Таким чином, множина R може бути получено отримано послідовним виконанням (зліва на право) операція об’єднання в співвідношенні (1), до тих пір, поки «протікаюче» не перестане збільшуватися по розміру при наступній операції об’єднання. З цього моменту наступні операції не будуть давати нових членів множині і, таким чином буде утворено досяжна множина R . Число об’єднань, яке потрібно виконати, залежить від графа, але, очевидно, що число p менше числа вершин в графі.

Матрицю досяжностей можна вистроїти так. Знаходимо досяжні вершини R для всіх вершин способом, наведеним вище покладемо , якщо , і =0 в протилежному випадку. Отримана таким образом матриця R являється матрицею досяжностей.

Матриця контрдосяжностей Q= виявляється наступним чином:

Контрдосяжною множиною Q графа G являється множина таких вершин, що із будь-якої вершини цієї множини можна досягнути вершину . Аналогічно побудови досяжної множини R на основі відношення (1) можна «сформулювати» множину Q , використовуючи наступний вираз:

(2)

де і т. д.

Операції виконуються зліва на право до тих пір, поки наступна операція об’єднання не перестане змінювати «поточну» множину Q .

Із визначень очевидно, що стовбець матриці Q (в якому , якщо , і в противному випадку) співпадає із рядком матриці R, тобто , де – матриця транспонована до матриці досяжностей R.

Приклад 20. Знайти матриці досяжностей і зворотніх досяжностей для графа G, приведеного на рис. 1.

Рис. 19

Матриця суміжності графа G має вид

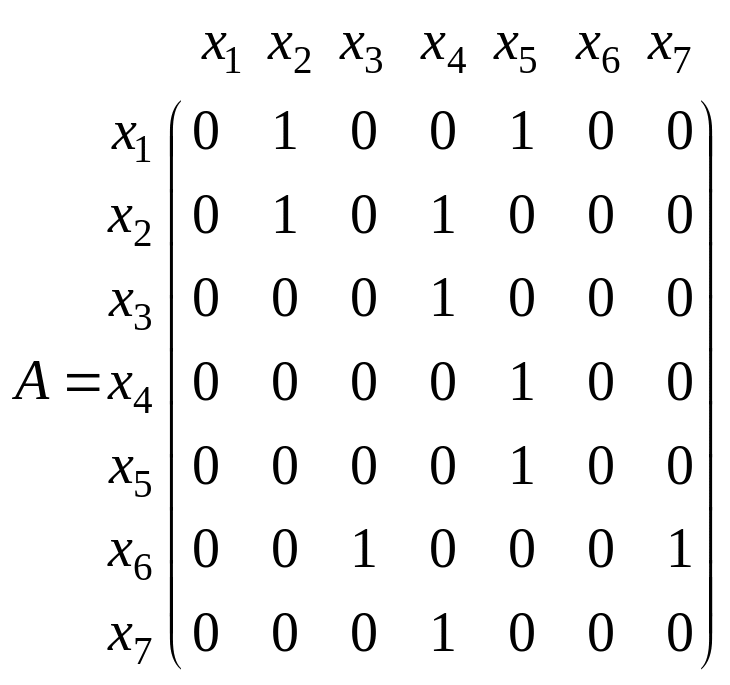
Множини досяжностей находяться з допомогою співвідношення (2.1):

,

,

,

,

,

.

З цього слідує що, матриця досяжностей буде мати вигляд

Матриця обернених досяжностей така:

Потрібно відмітити, що оскільки всі елементи матриць R і Q рівні 1або 0, то кожну стрічку можна зберігати в двійковому форматі, використовуючи одне (або більше) машинних слів. Таким чином знаходження матриць R і Q з вичисляючої точки зору являється дуже простою завданням, оскільки об’єднання множин в відповідності з виразами (1) і (2) і зрівняння поточних множин після кожного об’єднання, проведене для вияснення необхідності продовження процесу побудови відповідних множин, - все що можна здійснити на ЕОМ з допомогою однієї логічної операції .

Так як R є множиною вершин, досяжних із , а Q – множина вершин із яких можна досягнути , то R Q – множина таких вершин кожна із яких належить як мінімум до одного шляху слідуючому від до . Ці вершини називаються істотними або не від’ємними від відносно двох кінцевих вершин і . Всі інші вершини називаються несуттєвими або надлишковими, оскільки їх видалення впливає на шляхи від до .

Матриці досяжностей і зворотніх досяжностей, визначені вище, являються повними в тому сенсі, що на довжині шляхів від до не накладались ніякі обмеження. З іншої сторони можна визначити матриці обмежених досяжностей і контрдосяжностей – потрібно вимагати щоб довжини шляхів не перевищували деякого заданого числа. Ці обмежені матриці також можуть бути побудовані з допомогою співвідношень (1) і (2) – потрібно діяти точно так, як раніше, при знаходженні «неограничених» матриць, але тепер p буде верхньою границею можливих шляхів.