2. Алгебри булевих функцій

Розглянемо дві алгебри. Алгебру з операціями заперечення, кон’юнкції та диз’юнкції називають алгеброю Буля, а алгубру з операціями кон’юнкції та додавання за mod2 − алгеброю Жегалкіна.

Таблиця 1. Елементарні булеві функції

№ п/п	Позначення функції	Назва функції
			0	0	1	1
			0	1	0	1
		Кон’юнкція	0	0	0	1
		Диз’юнкція	0	1	1	1
		Імплікація	1	1	0	1
		Обернена імплікація	1	0	1	1
		Рівносильність	1	0	0	1
		Нерівносильність (сума за модулем 2)	0	1	1	0
		Функція Шеффера (інверсія кон’юнкції)	1	1	1	0
		Функція стрілка Пірса-Вебба (інверсія диз’юнкції)	1	0	0	0
		Інверсія імплікації	0	0	1	0
		Інверсія, обернена імплікації	0	1	0	0
		Повторення (змінна )	0	0	1	1
		Інверсія (функція НЕ )	1	1	0	0
		Повторення (змінна )	0	1	0	1
		Інверсія (функція НЕ )	1	0	1	0
		Одинична функція (константа 1)	1	1	1	1
		Нульова функція (константа 0)	0	0	0	0

Алгебри булевих функцій

Розглянемо дві алгебри. Алгебру з операціями заперечення, кон’юнкції та диз’юнкції називають алгеброю Буля, а алгубру з операціями кон’юнкції та додавання за mod2 − алгеброю Жегалкына.

Закони алгебри Буля:

• закони асоціативності

, ;

• закони комутативності , :

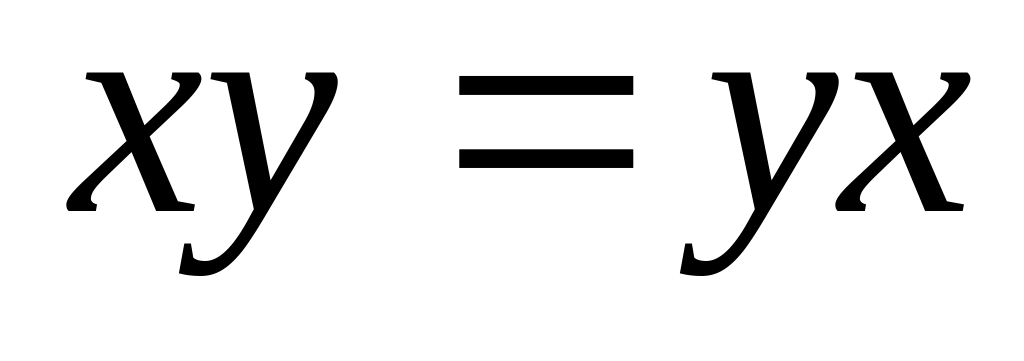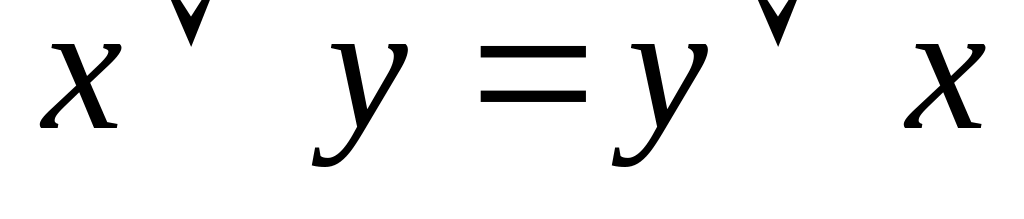• дистрибутивний закон для кон’юнуції щодо дизюнкції ;

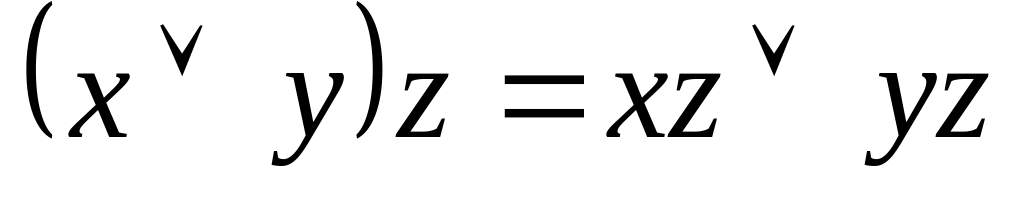• дистрибутивний закон для диз’юнкції щодо кон’юнкції ;

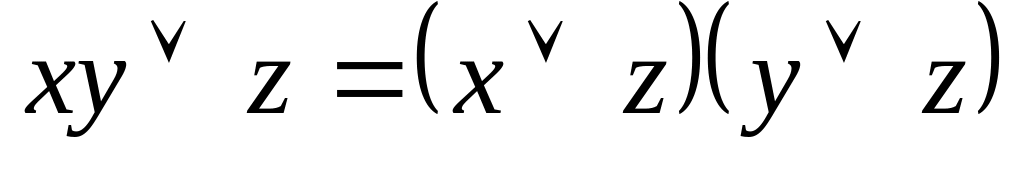• закон подвійного заперечення ;

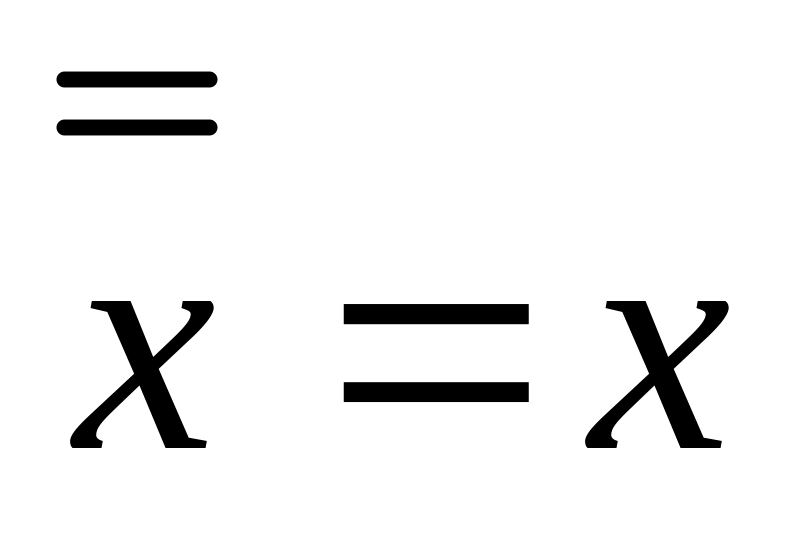• закони де Моргана , ;

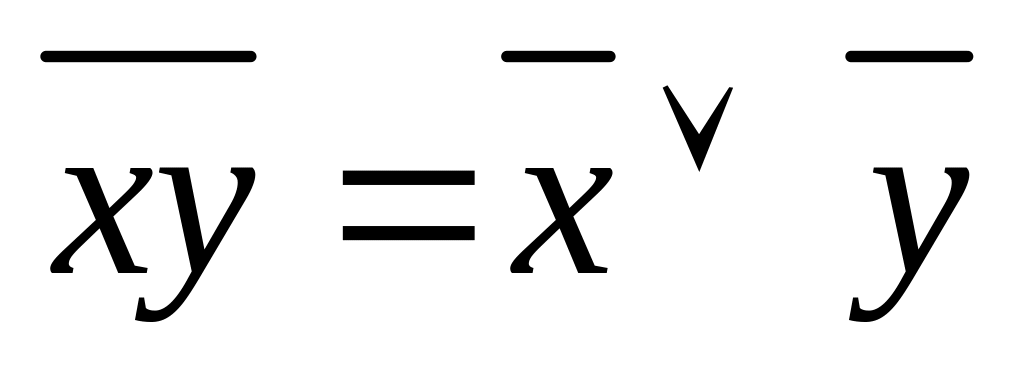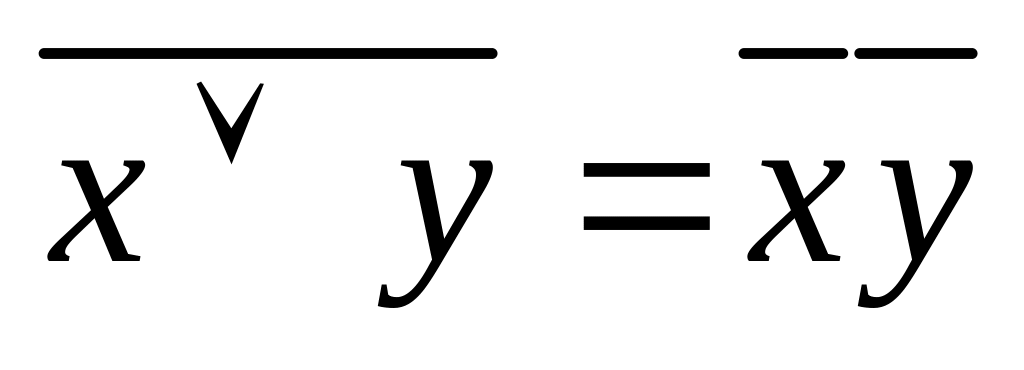• закони ідемпотентності , ;

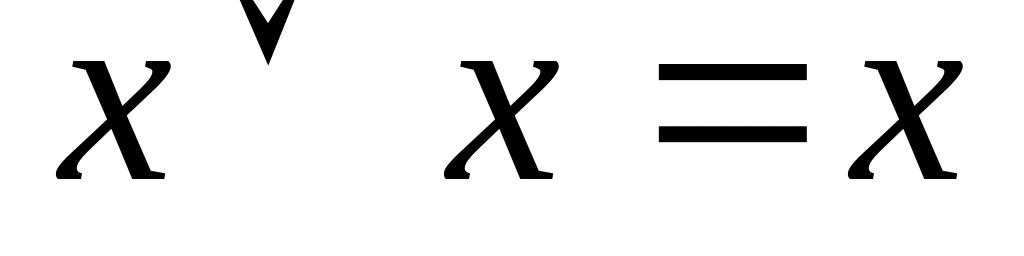• закони поглинання , ;

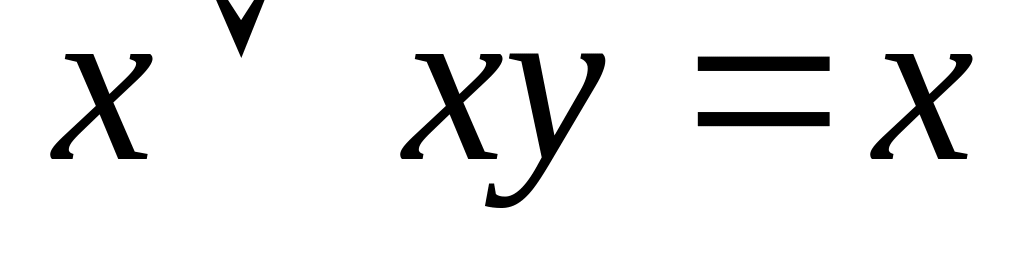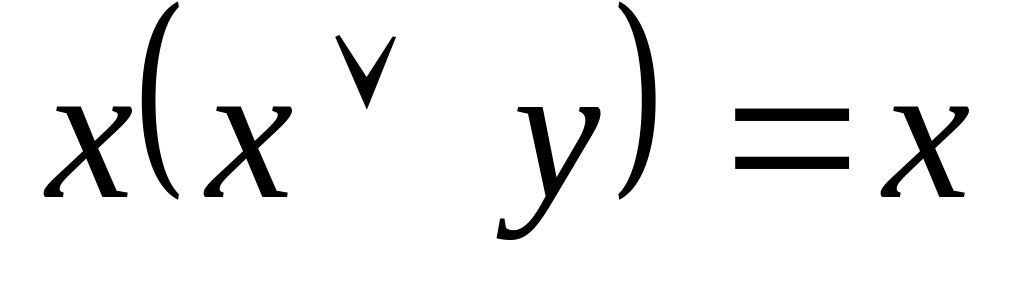• співвідношення для констант , , , , , ;

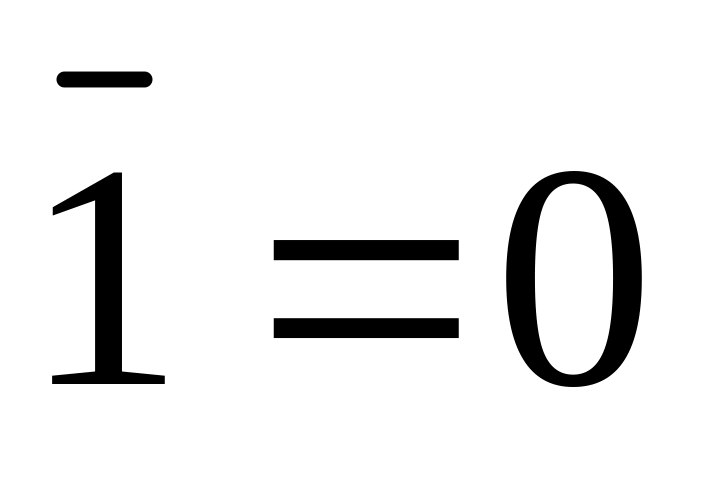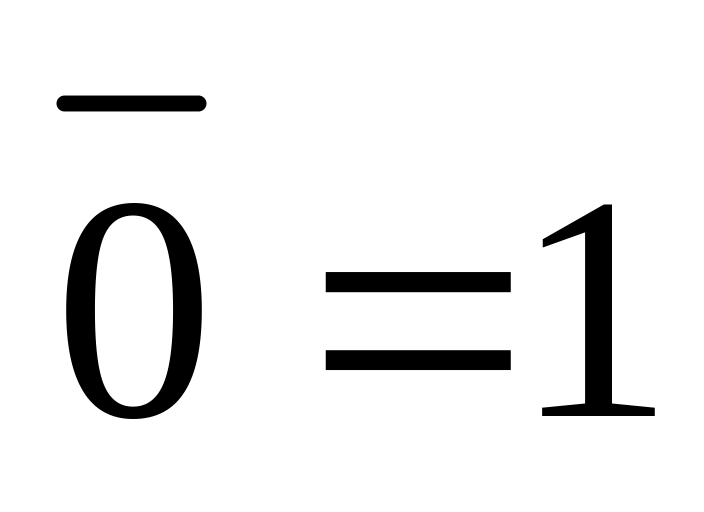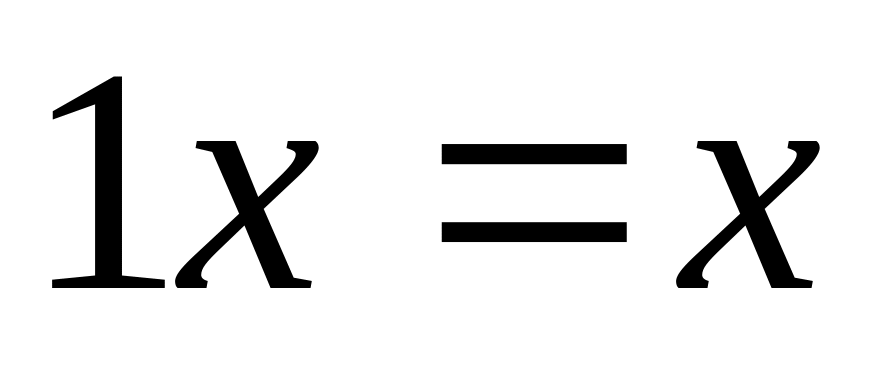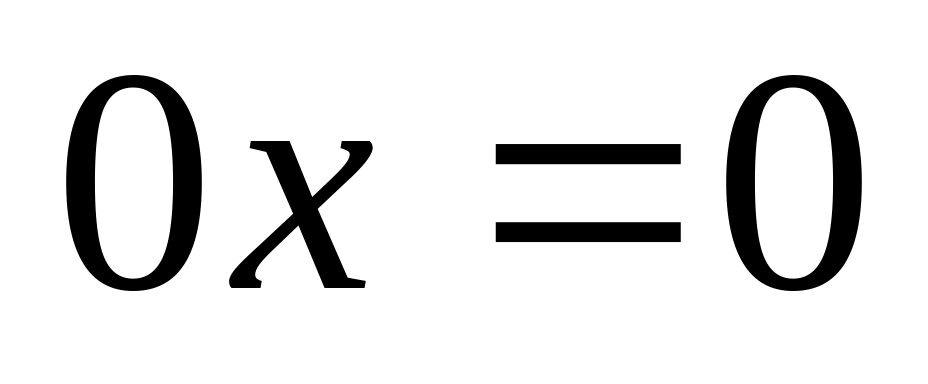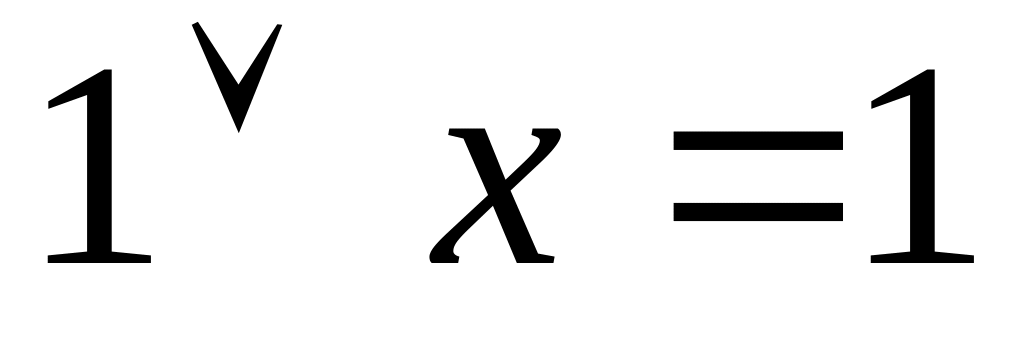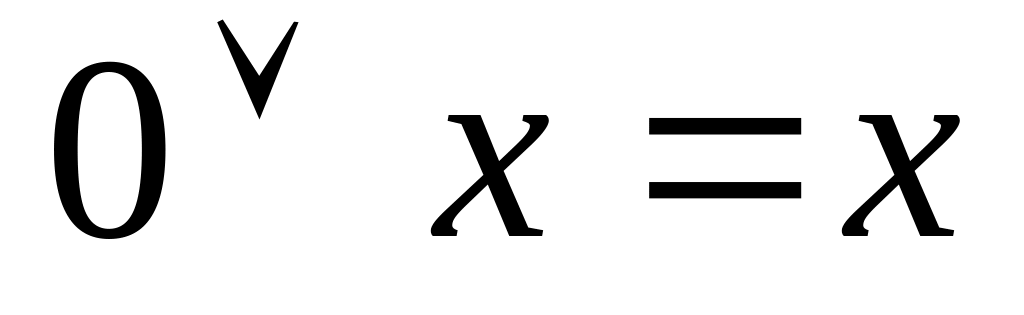• закон виключеного третього ;

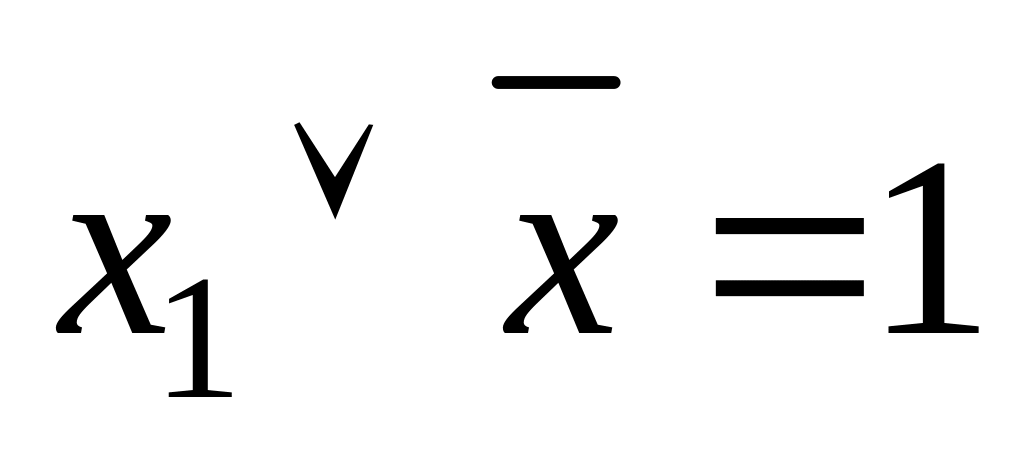• закон суперечності .

Закони алгебри Жегалкіна:

• закони асоціативності , ;

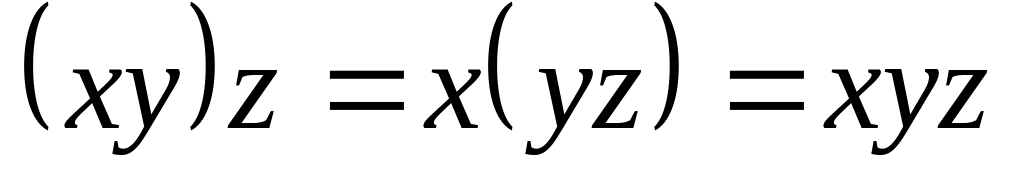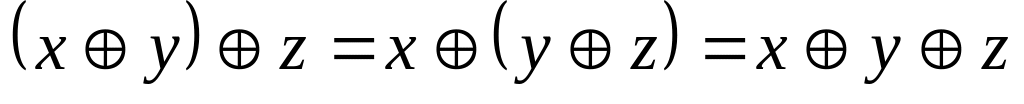• закони комутативності , ;

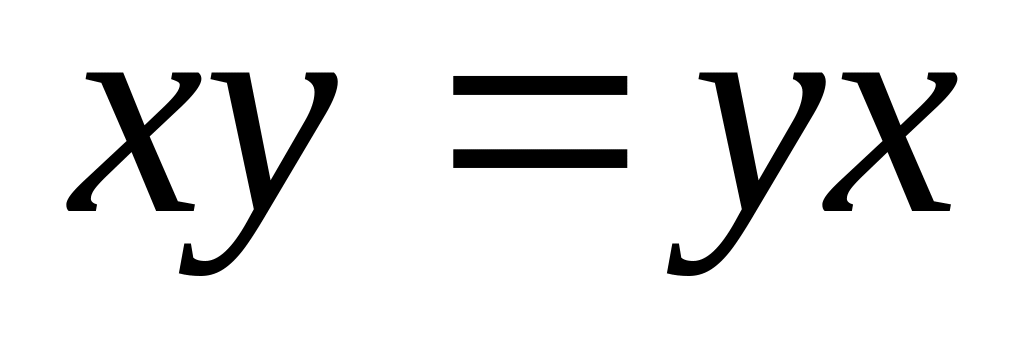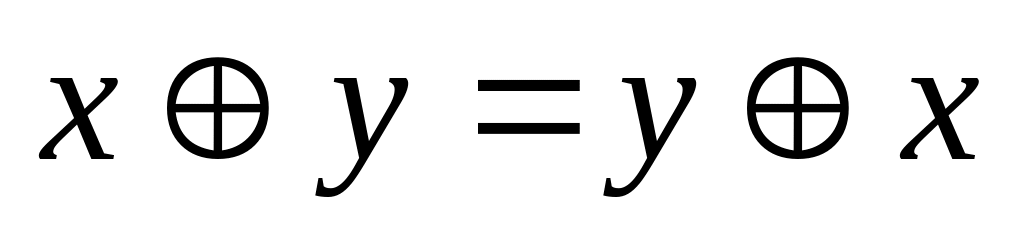• дистрибутивний закон для кон’юнкції щодо додавання за mod2 ;

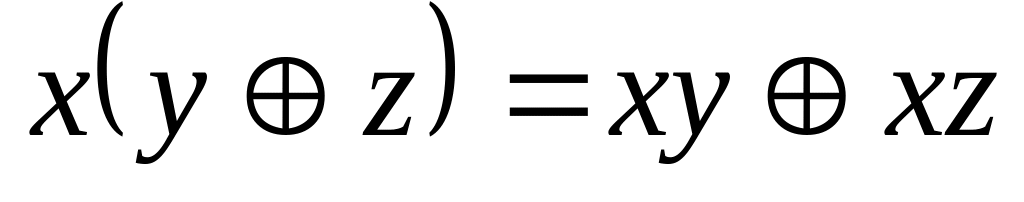• співвідношення для констант , , ;

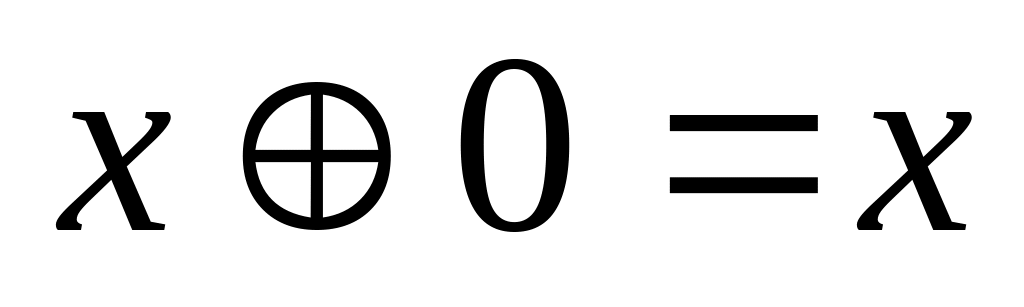• закон ідемпотентності для кон’юнкції ;

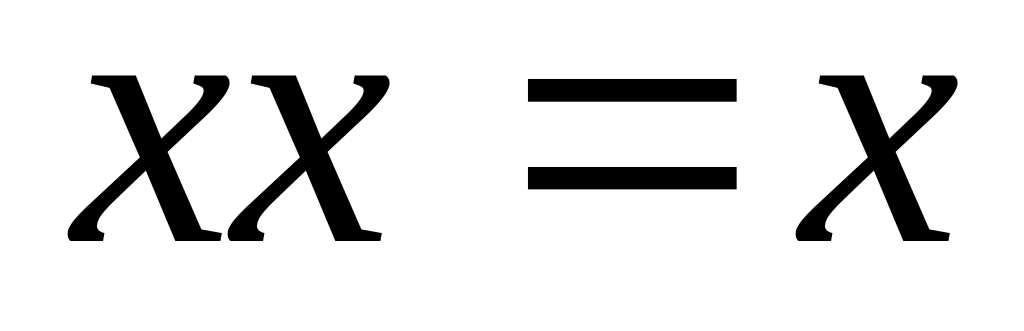• закон зведення подібних чденів у разі додавання за mod2 .

Правильність цих еквівалентностей можна довести зи допомогою таблиць.

Наведемо еквівалентності, які дають змогу перетворити будь-яку формулу булевої алгебри в рівносильну до неї формулу Жегалкіна й навпаки:

• ;

• ;

• .

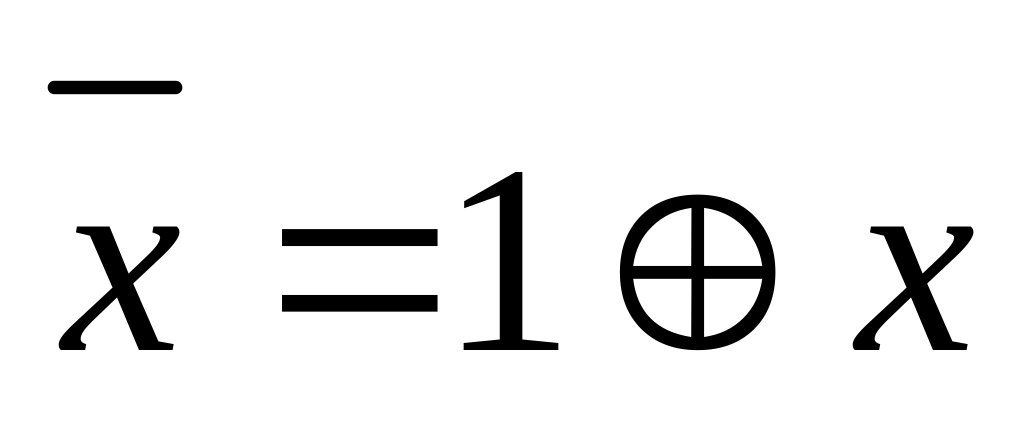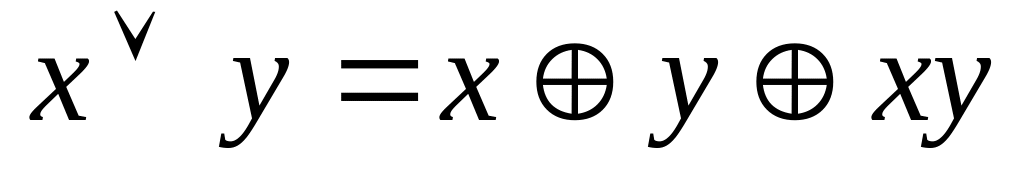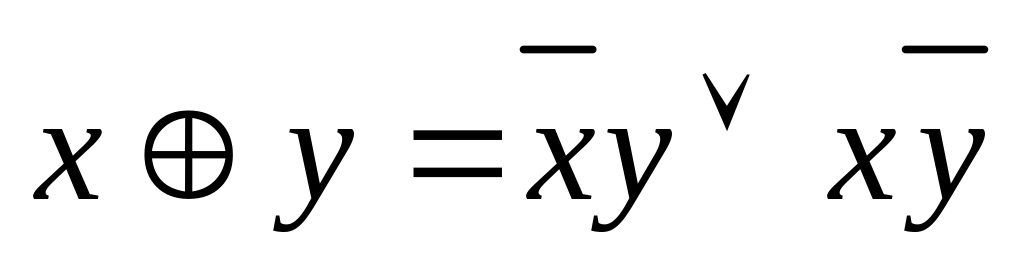За допомогою законів алгебри Буля та Жигалкіна можна спрощувати різні формули в цих алгебрах.

Диз’юнктивність нормальні формули

Уведемо позначення , де − параметр, який дорівнює 0 чи 1. Очевидно, що

Зауважимо, що .

Зафіксуємо множину змінних .

Елементарною кон’юнкцією називають вираз , де − змінні з множини , причому всі різна. Число називають кон’юнкції. У разі кон’юнкцію називають порожньою та вважають, що дорівнює 1.

Приклад. Елементарними кон’юнкції − це, наприклад , а вирази − не елементарні кон’юнкції.

Елементарну кон’юнкцію, яка місиь усі змінні з множини , називають конституентою одиниці. Інакше кажучи, конституента одиниці − це елементарна кон’юнкція з рангом . Очевидно, що всі різних конституент одиниці для фіксованої множини змінних стільки, скільки двійкових наборів з компонентами, тобто .

Диз’юнктивною нормальною формою (ДНФ) називають диз’юнкцію елементарних кон’юнкцій , у якій попарно різні.

Є алгоритм, який дає змогу для будь-якої формули булевої алгебри на основі тотожних перетворень знайти рівносильну, побудовану зі змінних і їх заперечень за допомогою самих лише кон’юнкцій і диз’юнкцій (тобто заперечення можуть стояти лише над змінними). Для використовують закони де Моргана та закон подвійного заперечення.

На другому етапі домагаються, щоб усі кон’юкції виконувалися рішене, ніж диз’юнкції, для чого розкривають дужки на підставі дистрибутивного закону для кон’юнкції або рівносильності (див приклад). Далі х використанням співвідношень для констант і закону суперечності вилучають нулі та, виходячи із законів ідемпотентності, об’днують рівні члени. Нв цьому процес отримання ДНФ закінчують.

Теорема. Будь-яку булеву функцію можна єдиним способом подати в ДДНФ.

Із доведення теореми випливає, що для функції, заданої таблицею, ДДНФ будують так: для кожного набору, на якому функція набуває значення 1, будують віддповідно йому конституентну одиниці; диз’юнкція всіх цих конституент − це ДДНФ даної функції.

Приклад. Побудуємо ДДНФ для функції, заданої табл.

Таблиця 1

х1	х2
0 0 1 1	0 1 0 1	1 0 0 1

Функція набуває значення 1 на наборах (00) і (11), отже .

Будь-яку ДНФ можна завести до ДДНФ розщепленням кон’юнкцій, які містять не всі змінні: якщо кон’юнкція не містить змінної , то

.

Приклад. Перетворимо ДНФ на досконалу. Застосувавши розщеплення для кон’юнкції , одержемо

.

Кон’юнктивні нормальні форми

Двоїстим способом, замінюючи в означеннях нулі одиницями й навпаки, диз’юнкції кон’юнкціями й навпаки, означають поняття елементарної диз’юнкції, конституенти нуля, кон’юнктивної нормальної форми, досконалої кон’юнктивної нормальної форми.

Елементарною диз’юнкцією називають вираз , у якому всі різні, . Число називають рангом диз’юнкції.

Кон’юнктивною нормальною формою (КНФ) називають кон’юнкцію елементарнихдиз’юнкцій , у якій усі різні.

Елементарну диз’юнкцію, яка містить усі змінні з множини , називають ституентою нуля.

Досконалою кон’юнктивною нормальною формою (ДКНФ) називають КНФ, у якій кожна елементарна диз’юнкція − конституента нуля.

Поліном Жигалкіна

Елементарну кон’юнкцію називають монотонною, якщо вона не містить заперечень змінних. Наприклад, − монотонні кон’юнкції.

Формулу

де − попарно різні монотонні кон’юнкції змінних із множини , називають поліномом Жегалкіном. Найбільший із рангів елементарнихкон’юнкцій, що входять у поліном, називабть степенем полінома. За окремим означенням 0 також уватимемо поліномом Жегалкіна.

Приклад. Формули − поліномом Жегалкіна, а − ні.

Теорема. Будь-яку булеву функцію можна єдиним способом подати у вигляді полінома Жегалкіна.

Метод невизначених коефіцієнтів. Для функції записують найзагальніший вигляд полінома Жегалкіна із невизначеними коефіцієнтами . Зокрема, поліном від двох змінних має загальний вигляд

,

а від трьох змінних −

.

Для кодного двійкового набору значень змінних записують рівнянь . Розв’язавши їх, отримують коефіціенти полінома .

Приклад. Побудуємо поліном Жигалкіна для функції . Прирівняємо значення функції та полінома на всіх чотирьох наборах значень змінних і одердимо систему рівнянь відносно неозначених коефіціентів:

,

,

,

.

Розв’язавши її, визначаємо, що й, отже, .

Побудова полінома Жегалкіна на основі рівносильних перетворень. Спочатку будують рівносильну фрмулу, к якій є лише операції та заперечення, а потім всюди замінюють на . Після цього тривіальними перетвореннями отримують поліном Жегалкіна.

Приклад. Побудуємо поліном Жегалкіна для функції . Використовуючи введені раніше еквівалентності, одержимо

.

Побудова полінома Жегалкіна за ДДНФ булевої функції. Цей спосіб грунтується на доведенні теореми. Його доцільність застосовувати тоді, коли функцію задоно ДДНФ або цю форму легко знайти.

Приклад. Побудуємо таким методом поліном Жегалкіна для функції . Спочатку перетворимо цю ДНФ на досконалу:

.

Повторивши доведення теореми маємо

Поліном Жегалкін має цікаву властивість, зручну для знаходження істотних змінних функцій.

Теорема. Усі змінні булевої функції,які входить у її поліном Жегалкіна, істотні.

Література:

1. Комп’ютерна дискретна математика: Підручник/ М.Ф. Бондаренко, Н.Ф. Білоус, А.Г. Руткас. – Харків: «Компанія СМІТ», 2004. – 480 с. с.42-52.

2. Нікольський Ю.В., Пасічник В.В., Щербина Ю.М. Дискретна математика. – К.: Видавнича група ВНV, 2007. – 368 с.

3. Зарипова Э.Р., Кокотчикова М.Г. Дискретная математика. Лекции по дискретной математике. Часть 1,2. – Издательство: РУДН, 2013. – 116 с.