
- •Закон больших чисел в форме Чебышева
- •Основное утверждение
- •Испытание практически достоверного события
- •Сжатие распределения с ростом числа слагаемых
- •Усиленный закон больших чисел.
- •Теорема Гливенко основная теорема статистики
- •Центральная предельная теорема Содержание теоремы
- •Различно распределенные слагаемые
Лабораторная работа N1
Теория вероятности и математическая статистика
Студент: Машеров Д.
Группа А-13-08
Преподаватель: Тигетов Д.Г.
Теорема Бернулли
Если проводится n независимых испытаний случайного событияA, вероятность которогоP(A) = p, то относительная частота/nпоявления событияA ( число появленийA) при большом nприближенно равна вероятностиp:
 .
.
, или

 при
при ,
,
если для любого >0 и для достаточно большихnсоотношение
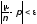 (1)
(1)
выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:
 при
при .
.
Пример.Бросание симметричной монеты.
Вероятность появления герба p=0.5.можно показать (с помощью центральной предельной теоремы), что, например, если n (1.5/)2, то соотношение (1) выполняется с вероятностью 0.997, а еслиn (1.3/)2, тос вероятностью 0.99; последняя в данном случае нас вполне устраивает как практическая достоверность. Положим= 0.1; тогда соотношение
| /n - 0.5 | < 0.1 (a)
выполняется
с вероятностью 0.99 при n 170.если=0.03,
то соотношение
170.если=0.03,
то соотношение
| / n - 0.5 | < 0.03 (б)
выполняется
с вероятностью 0.99 при n
 1850.
Бросание монеты моделируем генерацией
случайной величины,
принимающей значения 1 ("герб") и 0
("цифра") с вероятностями 1/2. Число
появлений "герба" вnиспытаниях
1850.
Бросание монеты моделируем генерацией
случайной величины,
принимающей значения 1 ("герб") и 0
("цифра") с вероятностями 1/2. Число
появлений "герба" вnиспытаниях
 ,
,
где k- результатk-го испытания.

Посчитаем число успехов(сумма всех значений), и среднее арифметическое:
Для 170 испытаний:
0.494 – 0.5 =0.041< 0.1.
Для 1850
0.481 – 0.5 =0.001< 0.03.
Оба результата удовлетворяют соотношениям (а) и (б).
Закон больших чисел в форме Чебышева
Основное утверждение
Одно из основных утверждений закона
больших чисел состоит в том, что значение
среднеарифметического
 случайных величин с равными математическими
ожиданиями
случайных величин с равными математическими
ожиданиями при большомn(при некоторых широких
условиях) оказывается приближенно
равнымa:
при большомn(при некоторых широких
условиях) оказывается приближенно
равнымa:

, или
 при
при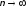 ,
,
если для любого >0 и достаточно больших nсоотношение
 (2)
(2)
выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:
 приn
.
приn
.
это одно из утверждений закона больших чисел.
Теоремы Чебышева.Если -
последовательность попарно независимых
случайных величин, имеющих конечные
дисперсии, ограниченные одной и той же
постоянной:
-
последовательность попарно независимых
случайных величин, имеющих конечные
дисперсии, ограниченные одной и той же
постоянной:
 ,
,
то для любого >0
 при
при .
.
Испытание практически достоверного события
Случайные величины распределены равномерно на отрезке [0,1]. Если значениезадавать произвольно, а число испытаний выбирать из условияn(9D/2), то (как нетрудно показать) соотношение (2) выполняется с вероятностьюP=0.997, а еслиn(5.4D/2) - то сP=0.98. Последняя нас устраивает, как практическая достоверность.
Положим 1 =0.1 и2 =0.02, определим два соответствующих значенияn1 =45 иn2 =1125, и проверим (2) экспериментально (в нашем случаеa=0.5). Выполнение аналогично п.1. При генерации случайных чисел нужно задать полное имя новой переменной, например, LIMIT.unif.
Задание. Проверить (2) экспериментально для экспоненциально распределенных слагаемых с M=1. Принять1 =0.2 и2 =0.05.
Выполнение:для экспоненциально
распределенных слагаемых с M=1
мы проверили утверждение, что



 ;
;

Оба результата удовлетворяют соотношениям.
Невыполнение закона больших чисел
Рассмотрим случайную величину,
распределенную по закону Коши с
плотностью (3)
(3)
Это распределение не имеет математического
ожидания. Для последовательности
независимых случайных величин,
распределенных по закону Коши (3), закон
больших чисел не выполняется. Если бы
среднеарифметическое

 сходилось с ростомnк какой-либо
константе, то, в силу симметрии
распределения, такой константой мог
быть только 0. Однако, 0 не является точкой
сходимости. Действительно, можно
показать, что при любом>0 и при любом сколь угодно большом
n
сходилось с ростомnк какой-либо
константе, то, в силу симметрии
распределения, такой константой мог
быть только 0. Однако, 0 не является точкой
сходимости. Действительно, можно
показать, что при любом>0 и при любом сколь угодно большом
n
 (4)
(4)
с вероятностью
 arctg.
Эта вероятность, как видно, не стремится
к 0 с ростомn. Например, если= 0.03, то вероятность выполнения (4) равна
приближенноP
0.98, т.е. событие (4) практически
достоверно, и можно уверенно ожидать
его выполнения с одного раза. Если
=1, то вероятность (4) равна 0.5, и
выполнение его хотя бы раз можно уверенно
ожидать, проделав 7 экспериментов (т.к.
вероятность невыполнения ни разу равна
(0.5)7 = 1/128). И это при любом фиксированномn, например,n = 1000. Проверим это
экспериментально.
arctg.
Эта вероятность, как видно, не стремится
к 0 с ростомn. Например, если= 0.03, то вероятность выполнения (4) равна
приближенноP
0.98, т.е. событие (4) практически
достоверно, и можно уверенно ожидать
его выполнения с одного раза. Если
=1, то вероятность (4) равна 0.5, и
выполнение его хотя бы раз можно уверенно
ожидать, проделав 7 экспериментов (т.к.
вероятность невыполнения ни разу равна
(0.5)7 = 1/128). И это при любом фиксированномn, например,n = 1000. Проверим это
экспериментально.
Сгенерируем 7 выборок объемом n=1000 и проверим (4) при=1.
Заготовим
таблицу 7v1000c, сгенерируем
выборки со значениями из закона Коши .
.
Определим среднее значение на всех 7 выборках:
Убеждаемся, что хотя бы в одной выборке модуль среднего превосходит 1.
![]()
В 1,4,5,6 выборках модуль больше 1.
График выборки:

Из-за скачков, среднее становится слишком большим.
Сжатие распределения с ростом числа слагаемых
Закон больших чисел в форме Чебышева означает, что распределение случайной величины

сжимается с ростом n. Если математические ожидания одинаковы, т.е. Mi=a,то сжатие происходит в окрестности точкиa.
Аналитическииллюстрировать сжатие
можно, если распределение для
 легко выписывается. Например, если i
распределены нормально N(a,
2), то случайная величина
легко выписывается. Например, если i
распределены нормально N(a,
2), то случайная величина распределена по N(a, 2/n).Построим графики плотностей дляn =1,
4, 25, 100 и=1,a
=1 (сделаем это в целях освоения пакета).
распределена по N(a, 2/n).Построим графики плотностей дляn =1,
4, 25, 100 и=1,a
=1 (сделаем это в целях освоения пакета).
Статистическиубедиться в сжатии
можно, наблюдая гистограммы при различных
значенияхn(например, дляn =10,
40, 160, 640). Сгенерируем kраз (например,
хотя бы k =20) случайную величину
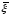 :
: и построим для этой выборки средних
гистограммуHn.Сравнивая
гистограммы для различныхn, мы
заметим сжатие (сделать самостоятельно).сжатие можно
увидеть определением для каждогоn по
и построим для этой выборки средних
гистограммуHn.Сравнивая
гистограммы для различныхn, мы
заметим сжатие (сделать самостоятельно).сжатие можно
увидеть определением для каждогоn по минимального
минимального min,максимального
min,максимального max
значений и размаха w
=
max
значений и размаха w
=
 max
-
max
-
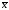 min
.
min
.
Аналитически:
Построим графики нормального распределения для n=1, 4, 25, 100, т.е. для= 0,5, 0,2, 0,1, аргументы меняются от -2 до 2




Видно, что графики сжимаются около 1.
2)Статистически
Получим к= 20 выборок объемомn= 640 из распределенияR[0, 1].
Посчитаем для n=10,40,160,640 среднее значения, и для них среднее отклонение, минимум и максимум:

График
разброса средних арифметических.

Видно, что с ростом испытаний средние арифметические значения становятся ближе к друг другу, причем уплотнение движется в сторону 0.5 – среднего значения одного испытания.
