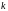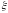- •Лабораторная работа № 1
- •Цель работы
- •Краткие теоретические сведения
- •Написание скриптов в математическом пакете MatLab
- •Исходные данные по вариантам
- •1.5. Порядок выполнения работы
- •1.6. Содержание отчета
- •1.6.2. Цель работы.
- •1.7. Вопросы для самоконтроля
- •Лабораторная работа № 2 «Типовые динамические звенья систем автоматического управления»
- •2.1. Цель работы
- •2.2. Краткие теоретические сведения
- •2.3. Написание скриптов в MatLab
- •2.4. Исходные данные
- •2.5. Порядок выполнения работы
- •2.6. Содержание отчета
- •2.6.2. Цель работы.
- •2.7. Вопросы для самоконтроля
2.3. Написание скриптов в MatLab
Задать в математическом пакете MatLab значения коэффициентов в соответствии с заданиями по вариантам, а также выражения для полиномов числителя и знаменателя каждого из рассмотренных типовых звеньев: пропорционального, интегрирующего, апериодического звена 1-го порядка, реального дифференцирующего и колебательного.
Затем сформировать передаточные функции каждого из типовых звеньев командой tf. Искомые характеристики систем могут быть найдены следующими командами MatLab
нахождение реакции системы на единичное ступенчатое воздействие .
step(W)
нахождение реакции системы на единичное импульсное входное воздействие;
impulse(W)
Амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой
nyquist(W)
Логарифмическую амплитудно-фазовую характеристику системы в полярных координатах можно получить воспользовавшись командой
bode(W)
Расчет полюсов системы производится в командном окне при помощи команды
pole(W)
Расчет нулей системы производится в командном окне при помощи команды
zero(W)
Все указанные характеристики можно построить командой ltiview.
Например, для колебательного звена:
k=1;
T=1;
xi=0.5;
B5=[k];
A5=[T^2,2*T*xi,1];
W5=tf(B5,A5);
ltiview({'step';'impulse';'bode';'nyquist';'pzmap'},W5);
После построения графиков необходимо щелчком мыши на диаграмме Найквиста вызвать контекстное меню и отключить пункт меню Show→Negative Frequencies.
Для сохранения полученных характеристик необходимо сначала преобразовать их в рисунок, для этого выбрать пункт меню File→Print to Figure, затем скопировать его в отчет из меню Edit→Copy Figure, после чего вставить в файл с отчетом.
Далее необходимо произвести исследование влияния значений коэффициентов колебательного звена на его характеристики. Для этого необходимо сформировать новые передаточные функции.
 для исследования
влияния значения коэффициента усиления
(увеличение коэффициента усиления
вдвое).
для исследования
влияния значения коэффициента усиления
(увеличение коэффициента усиления
вдвое).
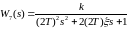 для исследования
влияния значения постоянной времени
(увеличение коэффициента вдвое).
для исследования
влияния значения постоянной времени
(увеличение коэффициента вдвое).
 для исследования
влияния значения коэффициента
демпфирования (уменьшение коэффициента
в два раза).
для исследования
влияния значения коэффициента
демпфирования (уменьшение коэффициента
в два раза).
 – консервативное
звено (коэффициент демпфирования
– консервативное
звено (коэффициент демпфирования
 ).
).
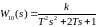 – апериодическое
звено второго порядка (коэффициент
демпфирования
– апериодическое
звено второго порядка (коэффициент
демпфирования
 ).
).
Построить их типовые характеристики командой ltiview, при этом выводить характеристики базового колебательного звена. На одном графике производить не более одной модификации звена. Например, для консервативного звена
B9=[k];
A9=[T^2,0,1];
W9=tf(B9,A9);
ltiview({'step';'impulse';'bode';'nyquist';'pzmap'},W5,W9);
После построения последнего графика необходимо настроить вывод графика переходной характеристики. Для этого открыть меню Edit→Viewer Preferences, выбрать вкладку Parameters, после чего настроить значение в поле Time Vector→Define stop time до такого значения, чтобы график переходной характеристики консервативного звена совершал 3-4 колебания.
2.4. Исходные данные
Исходные данные по вариантам представлены в таблице 2.1.
Таблица 2.1
Параметры динамических звеньев
Варианты |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0,5 |
1 |
2 |
3 |
1 |
2 |
1 |
0,5 |
1 |
2 |
|
2 |
1 |
0,5 |
1 |
0,2 |
1 |
3 |
1,5 |
2,5 |
3,5 |
|
0,6 |
0,2 |
0,4 |
0,5 |
0,4 |
0,3 |
0,4 |
0,6 |
0,2 |
0,5 |
Варианты |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1 |
2 |
1,5 |
2 |
1 |
1 |
2 |
1 |
1 |
3 |
|
2 |
4 |
0,8 |
3 |
0,5 |
1,5 |
2,5 |
3 |
1 |
2 |
|
0,4 |
0,3 |
0,5 |
0,6 |
0,5 |
0,3 |
0,2 |
0,4 |
0,6 |
0,5 |
Варианты |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
2 |
1 |
0,5 |
1 |
2 |
1 |
2 |
1,5 |
2 |
0,5 |
|
1 |
3 |
1,5 |
3,5 |
2,5 |
2 |
3 |
1 |
3,5 |
0,5 |
|
0,5 |
0,6 |
0,3 |
0,4 |
0,5 |
0,3 |
0,4 |
0,6 |
0,5 |
0,5 |