
- •Лабораторная работа № 1
- •Цель работы
- •Краткие теоретические сведения
- •Написание скриптов в математическом пакете MatLab
- •Исходные данные по вариантам
- •1.5. Порядок выполнения работы
- •1.6. Содержание отчета
- •1.6.2. Цель работы.
- •1.7. Вопросы для самоконтроля
- •Лабораторная работа № 2 «Типовые динамические звенья систем автоматического управления»
- •2.1. Цель работы
- •2.2. Краткие теоретические сведения
- •2.3. Написание скриптов в MatLab
- •2.4. Исходные данные
- •2.5. Порядок выполнения работы
- •2.6. Содержание отчета
- •2.6.2. Цель работы.
- •2.7. Вопросы для самоконтроля
1.5. Порядок выполнения работы
1.5.1. Ознакомиться с пакетом прикладных программ MATLAB (см. Приложение А).
1.5.2. В соответствии с вариантом задания (см. табл. 1.1) записать дифференциальное уравнение по аналогии с (1.1).
1.5.3. Получить систему в нормальной форме Коши в соответствии с (1.6).
1.5.4. Осуществить моделирование системы дифференциальных уравнений в математическом пакете MatLab, для чего реализовать два m-файла в соответствии с 1.3 (листинги 1.1 и 1.2).
1.5.5. Осуществить моделирование системы при следующих условиях:
а)
 .
Начальные условия нулевые. Продолжительности
интервалов моделирования подобрать
самостоятельно. На монитор выводить
графики сигналов
.
Начальные условия нулевые. Продолжительности
интервалов моделирования подобрать
самостоятельно. На монитор выводить
графики сигналов
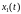 и
и
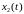 .
При этом график функции
будет являться графиком переходной
характеристики
.
При этом график функции
будет являться графиком переходной
характеристики
 ,
а график функции
,
а график функции
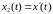 будет являться
графиком импульсной переходной функции
будет являться
графиком импульсной переходной функции
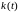 .
Скопировать результаты в отчет. Оценить
время переходного процесса и
перерегулирование, а также установившееся
значение переходной характеристики.
.
Скопировать результаты в отчет. Оценить
время переходного процесса и
перерегулирование, а также установившееся
значение переходной характеристики.
б) . Начальные условия ненулевые в соответствие с табл. 1.2. (внести соответствующие изменения в листинг второго скрипта в команде ode45, а также в названии рисунка title). На монитор выводить графики сигналов и . Скопировать результаты в отчет.
в)
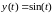 (внести изменение в первый скрипт,
заменив строку кода y=1;
на строку y=sin(t);).
Начальные условия нулевые (внести
соответствующие изменения в листинг
второго скрипта в команде ode45,
а также в названии рисунка title).
Продолжительности интервалов моделирования
подобрать самостоятельно. На монитор
выводить графики сигналов
и
.
Скопировать результаты в отчет.
(внести изменение в первый скрипт,
заменив строку кода y=1;
на строку y=sin(t);).
Начальные условия нулевые (внести
соответствующие изменения в листинг
второго скрипта в команде ode45,
а также в названии рисунка title).
Продолжительности интервалов моделирования
подобрать самостоятельно. На монитор
выводить графики сигналов
и
.
Скопировать результаты в отчет.
г) . Начальные условия ненулевые (внести соответствующие изменения в листинг второго скрипта в команде ode45, а также в названии рисунка title). Продолжительности интервалов моделирования подобрать самостоятельно. На монитор выводить графики сигналов и . Скопировать результаты в отчет.
1.5.6. Оформить отчет в соответствии с 1.6.
1.5.7. Подготовиться к защите лабораторной работы, для чего ответить на вопросы для самоконтроля 1.7 и разобрать соответствующие разделы, изученные на лекциях и семинарских занятиях.
1.6. Содержание отчета
Отчет должен содержать следующие разделы:
1.6.1. Титульный лист установленного образца, содержащий номер и название лабораторной работы, Ф.И.О. автора, учебную группу, Ф.И.О. и должность преподавателя, номер варианта, место и год выполнения работы
1.6.2. Цель работы.
1.6.3. Исходные данные в соответствии с вариантом задания.
1.6.4. Математическая модель динамической системы в форме обыкновенного дифференциального уравнения.
1.6.5. Полученная система дифференциальных уравнений в нормальной форме Коши.
1.6.6. Результаты моделирования системы.
1.6.7. Значение перерегулирования, установившегося значения и времени переходного процесса.
1.6.8. Выводы.
1.7. Вопросы для самоконтроля
1.7.1. Каким образом можно получить из обыкновенного дифференциального уравнения систему уравнений в нормальной форме Коши? Сколько уравнений будет в этой системе?
1.7.2. Назовите виды математических моделей системы?
1.7.3. Какой численный метод интегрирования реализует функция ode45?
1.7.4. Поясните принцип составления модели вход – выход?
1.7.5. На каких графиках построены переходная характеристика и импульсная переходная функция? Почему?
1.7.6. Как связаны между собой переходная характеристика и импульсная переходная функция системы?
1.7.7. Как связаны между собой сигналы и ? Почему?
1.7.8. Почему переходную характеристику и импульсную переходную функцию называют временными характеристиками?
