Тема 5. «Истечение жидкости из отверстия в тонкой стенке. Расчёт простого водопровода»

Задача 10.  Из открытого резервуара, в котором поддерживается постоянный уровень, по стальному трубопроводу (эквивалентная шероховатость ∆_э ) состоящему из труб различного диаметра d и различной длины L, вытекает в атмосферу вода, расход которой Q и температура t ^oС. Требуется: 1.Определить скорости движения воды и потери напора (по длине и местные) на каждом участке трубопровода. 2.Установить величину напора Нв резервуаре. 3.Построить напорную и пьезометрическую линии (можно без соблюдения масштаба).

Пусть d₁= d₃=15 мм, d₂=20 мм, длины всех трёх участков одинаковы и равны L₁= L₂= L₃= 1 м. Расход жидкости принимаем равным Q = 30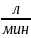 . Эквивалентную шерохова-тость труб принимаем равной ∆э= 0,1 мм

Решение.

.Запишем уравнение Бернулли для сечений 1-1 и 5-5: (только для этих сечений известны давления Р₁=Р_ат и Р₅=Р_ат): [ + + ]= [ + + ] + h_1-5

Рис.6 к задаче 10.

За нулевой уровень удобно принять плоскость, проходя-щую через ось трубопровода О-О. В этом случае z₁=Н, z₅=0. Средняя скорость в сечении 1-1 гораздо меньше скорости в сече-нии 5-5. Это следует из уравнения неразрывности струи:u₁ · S₁ = u₅ · S₅ ; u₅ = u_{4 -5} u₁ · (D²)= u₅ · (d₅²) следует, что скорость жидкости на первом участке 1-2 гораздо меньше ско-рости на участке 4-5 и ею можно пренебречь. Скорость в пятом сечении-это скорость на участке 4-5, в 4-ом –на участке 3-4, в третьем -2-3. В принципе, эти обозначения условны. При расчётах линейных и местных потерь напора, как будет показано ниже, выбираются скорости на конкретных участках.С учётом сказанного, уравнение Бернулли для данного случая принимает следующий вид: Н = α₅·[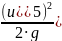 ]+ h_1-5 Величина напора в резервуаре идёт на создание скоростного напора и на преодоление всех потерь напора, чтобы донести нужный расход (задаваемый расход) до конца трубопровода.Коэффициент Кориолиса α₅= 1 для турбулентного течения и α₅=2 для ламинарного течения. Чтобы определить вид движения жидкости, рассчитаем число Рейнольдса, для участка 4-5.Re = ; при температуре 20⁰С плотность воды ρ = 10³ , динамическая вязкостьη = 10^-3 Па с.

Скорость на участке 4-5: u₅= = u₅= =2,83

Re_4-5 = Re_2-3 = =42460.

( = 1,5 10^-2 м) Это турбулентный режим движения, α₅=1.На участке 3-4 значение скорости u₃= = = = 1,59 .

Re_3-4= = 31800. Это так же турбулентный режим течения жидкости.

Полные потери напора на участке 1-5 ( h_1-5 ) складываются из линейных потерь на участках между сечениями 1-2, 2-3, 3-4 и 4-5 и местных потерь в сечениях 2-2, 3-3 и 4-4.

h_1-5 = h_1-2^л+h_2-3^л+h_3-4^л+h_4-5^л+h₂^м+h₃^м+h₄^м.

Для нахождения линейных потерь используем формулу Дарси:h^л= λ_тр · ( ) · .

На участке 1-2 (между сечениями 1-1 и 2-2) линейные потери малы и ими можно пренебречь. На участке 2-3, 3-4 и 4-5:

h_2-3^л= λ_2тр · ( ) · ; h_3-4^л= λ_3тр ·( ) · .

h_4-5^л=λ_4тр · ) · .

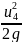Местные потери в сечениях 2-2, 3-3 и 4-4 находим по формуле Вейсбаха

h₂^м= ε₂· ; h₃^м= ε₃· ; h₄^м= ε₄· .

При внезапном расширении в сечениях (2-2) и (4-4) скорость выбирается после местного сопротивления (u₂ и u₄), а при внезапном сужении в сечении (3-3) скорость выбирается до местного сопротивления (u₂).Из справочника находим:ε₂ =0,5 (выход из бака в трубу). Для внезапного расширения при отноше-нии = 0,56 ε₃ =0,19. Для внезапного сужения при

= 0,56 ε₄ = 0,22.

Значения скорости на участке 2-3 и 4-5 одинаковы и равны: u₅ =u_2-3 = u_4-5= 2,83 . Для нахождения коэффициента гидравлического трения на участке 2-3 необходимо подобрать формулу из соответствующей области турбулентного режима. Для этого вначале рассчитаем значения: 10 = = 1500 и 560 = = 84100. 4000<42460 <84000. Это вторая область турбулентного течения Для расчёта коэффициента гидравлического трения выбираем формулу Альтшуля:

λ_2-3=0,11( + )^0,25= 0,11(0,0067+ 0,0016)^0,25 = 0,033 λ _3-4=0,11( + )^0,25= 0,11(0,005 + 0,002)^0,25 =0,032. λ_4-5= λ_2-3=0,033

Расчёты показывают, что коэффициент линейных (гидравлических) потерь по всей длине трубы примерно одинаков: λ=0,03.

Находим линейные потери напора на всех трёх участках:

h_2-3^л= h_4-5^л=λ_2тр· ) · ;

h_2-3^л = 0,03·( ) · [ ] = 0,82 м.

h_3-4^л= λ_2тр · ) · .

h_3-4^л = 0,03· ( ) · [ ] = 0,19 м.

Находим местные потери:

h₂^м= ε₂· =0,5·[ ] = 0,20 м

h₃^м= ε₃· = 0,19· ] = 0,08 м .

h₄^м= ε₄· ) =0,22 · ] = 0,09 м.Полные потери напора на участке 1-5:

h_1-5 = h_1-2^л+h_2-3^л+h_3-4^л+h_4-5^л+h₂^м+h₃^м+h₄^м.

h_1-5 = 0+0,82 м +0,19 м+ 0,82 м+0,20 м+0,08 м+0,09 м=2,2 м. Величина напора в резервуаре:

Н = α₅·[ ]+ h_1-5 = [ ]+2,2 м = 0,41 м +2,2 м = 2,61 м.

Вернёмся ещё раз к уравнению Бернулли: [ + + ]= [ + + ] + h_1-2

В левой части сумма + + называется напором в первом сечении. Он всегда больше, чем напор во втором сечении + + на величину потерь h_1-2 . Следовательно, чтобы найти напор во втором сечении, надо из значений напора в сечении 1 вычесть потери напора.

Напорную . линию строим следующим образом. Откладываем вдоль вертикальной оси(трубопровод начинается в сечении (2-2)) Н= 2,61 м. В сечении (2-2) теряется на местном сопротивлении (вход в трубу) h₂^м=0,20 м . При движении жидкости по трубе на участке между сечениями (2-2) и (3-3) в виде линейных потерь напора теряется h_2-3^л=0,82 м. Местные потери напора в сечении (3-3) равны h₃^м=0,08 м.

Линейные потери на участке (3-4) составляют h_3-4^л= 0,19 м. Местные потери в сечении (4-4) h₄^м=0,09 м. Линейные потери на участке (4-5) h_4-5^л=0,82 м. Соединяем полученные точки и строим напорную линию. Для построения пьезометрической линии из значений напора в соответствующих точках вычитаем скоростной напор ( ). На участках (2-3) и (4-5) = 0,41 м, а на участке (3-4) скоростной напор = 0,13 м.

На участке (4-5) скоростной напор =0,41 м. Соеди-няем полученные токи прямыми и получаем пьезометрическую линию.

Рис. 7. Примерное изображение напорных линий (полного и пьезометрического напоров).

Примечание: рисунок выполнен не в масштабе.