Тема 4 : «Основы газодинамики»

Основной отличительной особенностью движения газа по трубам от движения ка­пельных жидкостей заключается в том, что капельные жидкости характеризуются малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства прак-тических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости.

При движении газа таких допущений делать нельзя. Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных по-терь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неоди­наковы в различных сечениях газопровода. Рассмотрим наибо-лее простой случай газопро­вода (воздуховода) – трубы одинакового диаметра (простой газопровод S = const) при установившемся движении газа. Тогда в соответствии с уравнением не-раз­рывности потока газа массовый расход газа вдоль газопровода является величиной посто­янной = const. При этом объёмный расход Q_v газа будет меняться от одного сечения газопрово-да к другому, т.к. плотность газа зависит от давления, которое по длине газопро­вода меняется. При этом должна изменяться и температура газа по длине газопровода, и, как след­ствие, также и вязкость газа. Однако для решения практических задач движе-ние газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизо­ляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёз­ным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = const  и η = const. При таких условиях: = 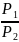. Для всего потока постоянным будет число Рейнольдса, и, как следствие, будут одинаковым коэффи­циенты трения и гидравлических сопротивлений по длине потока.

Объёмный расход: Q_v = . в этом случае меня-ется от сечения к сечению. Тогда скорость движения газа также будет меняться вдоль длины газопровода. Так как массовый расход = 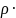u S = const (масса газа, движущегося по трубе, не меняется от сечения к сечению), то при постоянном диаметре трубы (S = const )скорость и плотность в сечениях связаны соотношением:

= . u = = = .

Число Рейнольдса: Re = = .

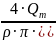Отметим, что в последнем выражении все величины, входящие в правую часть ра­венства, являются величинами постоянными, отсюда: Re = const.   По этой причине для определения величины потерь напора можно воспользоваться обычным уравнением Бернулли. Для горизонтальной трубы одинакового диаметра линейные потери определяются как: 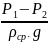= h_λ. Средняя плотность определяется как сумма = .

Линейные потери можно определить, как и в случае с жидкостью по формуле Дарси:

h_λ= . В качестве скорости берут среднюю скорость u = 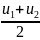. Коэффициент линейных потерь (движение турбулентное, Re ≥ 4000) можно определить по формуле Альтшуля: =0,11 · ( + )^0,25 или Блазиуса (для гидравлически гладких труб) = . Эквивалентную шероховатость берут из таблиц для жидкости.

Задача 8.Массовый расход транспортируемого газа по трубе диаметром 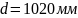составляет = 180 . Определить скорости движения газа в начальном и конечном сечениях, если плотность газа уменьшилась с = 45 до = 25 .

Решение.

Находим скорость движения газа в начальном сечении (на начальном участке газопровода):

u₁ = = = = = 4,9 .

В конечном сечении (на конечном участке газопровода):

u₂ = = = = = 8,8 .

Вывод: уменьшение плотности газа вследствие его расширения за счёт падения давления (потери энергии на преодоление сил трения) приводит к увеличению скорости его движения при неизменном диаметре. В жидкостях в таких условиях скорость не меняется, так как жидкость практически несжимаема.

Задача 9.Определить потери давления на участке прямого газопровода длиной 100м и диаметром 1020 мм, ес-ли массовый расход газа (азота) составляет = 180 , а плотность газа уменьшилась с = 45 до = 25 . Труба шероховатая, эквивалентная шероховатость составляет ∆_э=0,1 мм (новая стальная труба). Коэффициент динамичес-кой вязкости (для азота) при нормальных условий принять равным η = 17,8 10^-6 Па с.Для определения коэффициента линейных потерь λ_тр использовать формулу для жидкости.

Решение.

Для определения потерь давления используем уравнение Бернулли для трубы одинакового диаметра и уравнение Дарси для линейных потерь напора:

= h_λ и h_λ= .

Определим средние значения плотности и скорости по длине газопровода:

ρ_ср = = 35 . u = = 6,85 .

Число Рейнольдса:

Re= = = 12,6 10⁶

Так как число Рейнольдса больше 560 (5,7 10⁶), то для нахождения коэффициента гидравлического трения исполь-зуем формулу Альтшуля в виде:

=0,11 · ( + )^0,25.

=0,11 · ( )^0,25 = 0,11 (0,98 10^-4)^0,25 = 0,011.

Находим падение давления на данном участке газопровода:

Р₁ – Р₂ = ρ_ср = 35 = 886 Па.