Киреев Б.Н.

Основы гидропривода. Гидравлические

и пневматические системы.

1. Методика решения типовых задач.

При решении многих проблем в самых разнообразных отраслях промышленности часто при-ходится встречаться с вопросом о движении различных жидкостей и газов, а также с вопросом о силовом (механическом) их воздействии на те или другие поверхности и на обтекаемые ею твер-дые тела.

Изучение законов движения жидкостей и газов привело к созданию различных гидро- и пневмоустройств, широко используемых в настоящее время на практике. Наибольшее распрос-транение получили гидравлические (гидронасосы, гидродвигатели) и пневматические (пнев-модвигатели) машины.

Расчёты проводятся с использованием единиц измерения системы СИ. В отдельных случа-ях используются внесистемные единицы. В большинстве задач решения снабжены рисунками и подробными пояснениями.

Цель:

- изучить методику решения задач по гидравлике, газодинамике, гидравлическим машинам, гидроприводу;

- использовать полученные знания для выполнения самостоятельной (контрольной) работы.

Задание 1. Прежде чем приступать к изучению методики решения задач, необходимо изучить лекционный материал по данной тематике.

Задание 2. Изучить методику решения типовых задач, используя приведенные ниже примеры

Задание 3. Использовать данную методику при выполнении самостоятельной и конт-рольной работы. Варианты работ и контрольные задания приведены ниже.

Основы гидравлики

Тема 1: « Физические свойства жидкостей»

Задача 1.Определить коэффициент динамической и кинематической вязкости воды, если шарик d= 2мм , из эбонита, плотность которого ρ_ш=1,2· 10³ падает в воде с постоянной скоростьюu = 0,33 . Плотность воды ρ_ж=10³ .

Решение.

При движении шарика в жидкости с постоянной скоро-стью результирующая сила, равная сумме трёх сил (силы сопро-тивления движению F_c, силы тяжести F_т и выталкивающей силы F_выт) равняется нулю (согласно второму закону Ньютона F_рез= m•a=0, так как ускорение равно нулю). F_рез= F_т- F_выт-F_с = m•a=0 (1) ОтсюдаF_c= F_т- F_выт (2)

Сила сопротивления определяется по формуле Стокса: F_c= 6π·r·η·u = 3π· d· η· u. (3) Вес шарика определяется по фор-муле: F_т=mg = ρ_ш·V·g = ρ_ш · ( ) · g. (4) Выталкивающая сила равна весу вытесненной жидкости: F_выт= ρ_ж· V· g = ρ_ж· ( ) · g (5) Подставляем в формулу (2) значения сил из (3), (4) и (5), получаем:

Рис. 1 к задаче 1.Схема сил, действующих на падающее равномерно тело в жидкости.

3π· d· η· u = ρ_ш· ( ) · g – ρ_ж· ( ) · g(6) Из формулы (6) находим значение динамической вязкости воды: η = =

η = 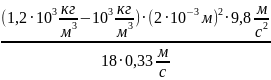= 1,32 · 10^-3 Па · с. Коэффициент кинематической вязкости: χ = = =1,32 · 10^-6 .

Ответ: коэффициент кинематической вязкости воды при комнатной температуре χ =1,32 · 10^-6 .

Задача 2.Определить избыточное давление на дне океана, глубина которого Н=10 км, приняв плотность морской воды ρ₀ = 1025 и считая ее несжимаемой. Определить плот-ность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости к=2020 МПа.

Решение

Избыточное давление на глубине Н без учёта сжимаемости воды:

Р = ρgH= 1025 •9,8 •10⁴ м = 10,04 •10⁷ Па = 100,4 МПа. Модуль объёмной упругости k = - ∙ v. Сжимаемость жидкости: β_р= = - · . Заменяя значения бесконечно малых изменений dV на значения конечных изменений объёма ∆V, находим значения сжимаемости: β_р= 1/к = - · . β_р = = = 4,95 •10^-10( ). Конечное значение объёма V= V₀·(1- β_р·∆p). По определению удельного объёма υ = . Следовательно, при давлении Р:

ρ = = ;

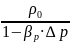ρ = =1079

Ответ: значения плотности морской воды на глубине 5 км ρ = 1079 .