Работа № 5. Критерий хи-квадрат проверки гипотез

Критерий хи-квадрат Пирсона является весьма общим методом построения тестов для проверки различных гипотез. Рассмотрим исходную схему.

1. Проверка простой гипотезы о вероятностях

Обозначим:

A₁, ..., A_m-m возможных исходов некоторого опыта; p₁, ..., p_m - вероятности cooтветствующих исходов, ;

n - число независимых повторений опыта;

n₁, ..., n_m - число появлений соответствующих исходов в n опытах, ;

p, ..., p - гипотетические значения вероятностей, p> 0, .

Требуется по наблюдениям n₁,...,n_m проверить гипотезу Н о том , что вероятности p₁, ..., p_m имеют значения p, ..., p, т.е.

Н: p_i= p, i=1, ...,m.

Оценками для p₁, ..., p_m являются =n₁ /n,..., =n_m/n. Мерой расхождения между гипотетическими и эмпирическими вероятностями принимается величина

,

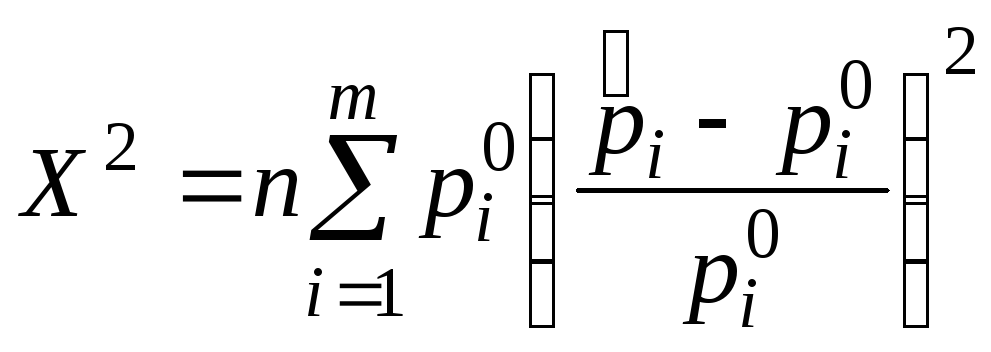которая с точностью до множителя n есть усредненное с весами p значение квадрата относительного отклонения значений от p. Статистика X² называется статистикой хи-квадрат Пирсона. Для ее вычисления используются две формулы:

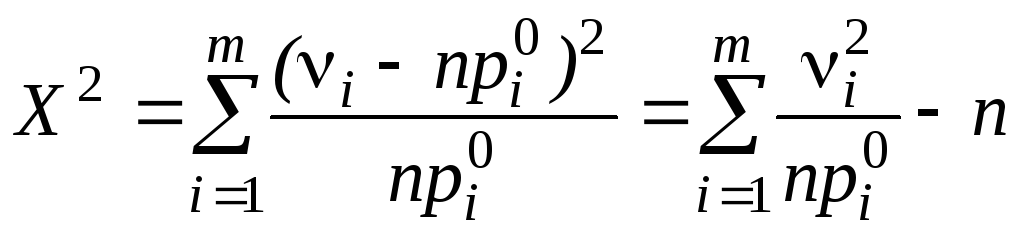. (1)

Условно статистику можно записать так:

Н - наблюдаемые частоты n_i, Т - теоретические (ожидаемые) частоты np. Поскольку по закону больших чисел® p_i при n®¥, то

.

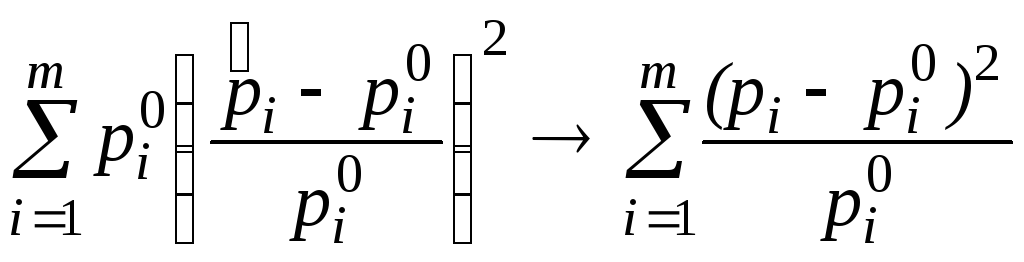Последняя величина равна 0, если верна Н; если же Н не верна, то X² ®¥.

Процедура проверки гипотезы состоит в том, что если величина X² приняла “слишком большое” значение, т.е. если

X² ³ h, (2)

то гипотеза Н отклоняется; если это не так, будем говорить, что наблюдения не противоречат гипотезе. На вопрос, что означает “слишком большое” значение, отвечает

Теорема К. Пирсона. Если гипотеза Н верна и p_i⁰ > 0,i=1,...,m, то при n® ¥ распределение статистики Х² асимптотически подчиняется распределению хи-квадрат с m- 1 степенями свободы, т.е.

Р{ X² < x / H } ® F_m-1(x) º P{ c²_m-1< x }.

Порог h выберем из условия: вероятность ошибки первого рода должна быть малой - равной выбираемому значению a - уровню значимости:

P{ отклонить H/ H верна} = P{X ² ³h / H}@P{c²_m-1 ³ h} =a,

откуда

h = Q(1-a, n -1) (3)

- квантиль уровня 1-a распределения хи-квадрат с m -1 степенями свободы.

Процедура (2) - (3) проверки Н может быть записана иначе: гипотеза Н отклоняется, если

P{c²_m-1 ³ X²} £ a, (4)

т.е. если мала вероятность получения (при справедливости Н) такого же расхождения, как в опыте (т.е. X²), или ещё большего. Вероятность слева в (4) называется минимальным уровнем значимости (при любом значении a, большем P{X²_m-1³ X²}, гипотеза, очевидно, отклоняется).

Замечание. Теорему Пирсона можно применять, если все ожидаемые частоты

np³10,i=1, ...,m; (5а)

если m порядка десяти и более, достаточно выполнения

np ³ 4,i=1, ...,m. (5б)

Если (5) не выполняется, необходимо некоторые исходы А_i объединять

2. Проверка сложной гипотезы о вероятностях

Пусть A₁, ...,A_m -m исходов некоторого опыта, n - число независимых повторений опыта, n₁,...,n_m - числа появлений исходов. Проверяемая гипотеза Н предполагает, что вероятности исходов P(A_i) являются известными функциями p_i(a) k-мерного параметра a = (a₁,...,a_k), т.е.

Н: Р(А_i) = p_i(a), i = 1, ..., m,

но значение а неизвестно.

Для проверки гипотезы Н определим статистику

(6)

По теореме Фишера, если Н верна, то при n ® ¥ распределение статистики Х² асимптотически подчиняется распределению хи-квадрат с числом степеней свободы f = m -1- k, и потому отклоняем Н, если

³h, (7)

где h = Q(1-a, f) - квантиль уровня 1- a распределения хи-квадрат с числом степеней свободы f; такой порог обеспечивает выбранный уровень a вероятности P(отклонить Н / Н) ошибки 1-го рода. Если (7) не выполняется, делаем вывод, что наблюдения не противоречат гипотезе. Распределению хи-квадрат с f = m -1-k степенями свободы асимптотически подчиняется также статистика

, (8)

где - оценка максимального правдоподобия для а, и потому в (7) может быть использована статистика (8) вместо (6). Процедура (7) может быть записана иначе: если

P{c_f² ³ X²} £ a (9)

то гипотеза Н отклоняется.