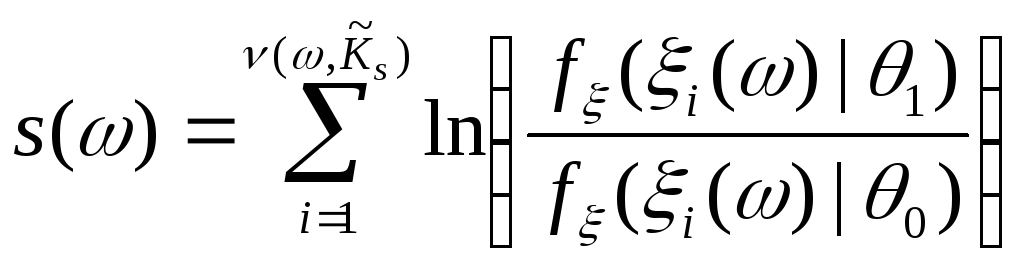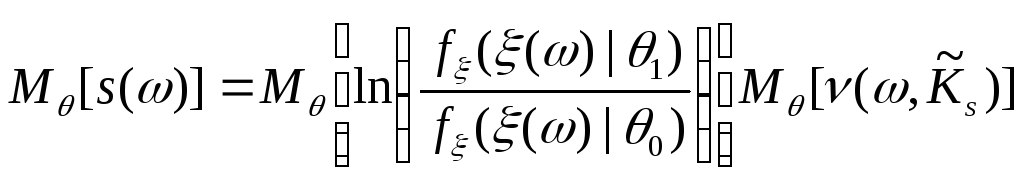3. Последовательный критерий отношения вероятностей.
В параграфах 1 и 2 рассматривались задачи
проверки параметрических гипотез, в
которых количество случайных величин
![]() в наблюдении
в наблюдении![]() являлось фиксированным числом.
являлось фиксированным числом.
Представим себе задачу проверки
параметрической гипотезы
![]() и альтернативной гипотезы
и альтернативной гипотезы![]() ,
в которой объем наблюдения
,
в которой объем наблюдения![]() не фиксирован и наблюдения можно получать
последовательно: на нулевом шаге
наблюдение отсутствует, на первом шаге
наблюдением является одна случайная
величина
не фиксирован и наблюдения можно получать
последовательно: на нулевом шаге
наблюдение отсутствует, на первом шаге
наблюдением является одна случайная
величина![]() ,
на втором шаге наблюдением является
две случайные величины
,
на втором шаге наблюдением является
две случайные величины![]() ,
и так далее, на
,
и так далее, на![]() -ом
шаге наблюдением является вектор
-ом
шаге наблюдением является вектор![]() ,
и при этом число шагов ничем не ограничено.
,
и при этом число шагов ничем не ограничено.
Подобная трактовка наблюдения приводит к новому классу критериев, которые называются последовательные критерии(раздел статистики, в котором изучаются последовательные критерии, называетсяпоследовательный анализ). На каждом шаге последовательный критерий принимает в точности одно из следующих решений:
1. остановиться и принять гипотезу
![]() (отклонить
(отклонить![]() );
);
2. продолжить и получить следующее наблюдение;
3. остановиться и принять гипотезу
![]() (отклонить
(отклонить![]() ).
).
Наилучшие критерии, рассмотренные в
предыдущих параграфах (минимаксный,
байесовский и равномерно наиболее
мощный), в каком-то смысле тоже являются
последовательными критериями, которые
на первых
![]() шагах выбирают «продолжить и получить
следующее наблюдение», а на
шагах выбирают «продолжить и получить
следующее наблюдение», а на![]() шаге принимают
шаге принимают![]() либо
либо![]() и останавливаются. Каждый из рассмотренных
критериев оказывался «наилучшим» в
каком-то смысле: минимаксный критерий
минимизировал наибольшую из двух
вероятностей ошибок, байесовский
критерий минимизировал значение функции
средних потерь, равномерно наиболее
мощный минимизировал вероятность ошибки
второго рода при условии ограниченной
вероятности ошибки первого рода.
и останавливаются. Каждый из рассмотренных
критериев оказывался «наилучшим» в
каком-то смысле: минимаксный критерий
минимизировал наибольшую из двух
вероятностей ошибок, байесовский
критерий минимизировал значение функции
средних потерь, равномерно наиболее
мощный минимизировал вероятность ошибки
второго рода при условии ограниченной
вероятности ошибки первого рода.
Каждый последовательный критерий, как и всякий критерий, также обладает величинами вероятностей ошибок первого и второго родов, и дополнительно характеризуется средним количеством шагов, проделанных до момента остановки и принятия одной из гипотез. Очевидно, что в классе последовательных критериев с заданными величинами вероятностей ошибок первого и второго родов наилучшим следует считать тот критерий, который в среднем требует наименьшего числа шагов до остановки. Оказывается, в некоторых случаях такие критерии существуют и могут быть получены в явном виде как последовательные критерии отношения вероятностей.
Рассмотрим основные положения
последовательного анализа на примере
следующей простой задачи различения
двух простых гипотез. Поскольку количество
случайных величин в наблюдении не
ограничено, то следует считать, что
задана последовательность случайных
величин
![]() для которой определена последовательность
функций распределения
для которой определена последовательность
функций распределения![]() первых
первых![]() случайных величин:
случайных величин:
![]() ,
,
![]() .
.
Будем считать, что каждая из функций
![]() удовлетворяет условиям (C1)
и (C2) (указанным в параграфе
2).
удовлетворяет условиям (C1)
и (C2) (указанным в параграфе
2).
Основная гипотеза
![]() заключается в том, что
заключается в том, что![]() ,
а альтернативная гипотеза
,
а альтернативная гипотеза![]() заключается в том, что
заключается в том, что![]() .
.
Каждый последовательный критерий
![]() на
на![]() -ом
шаге располагает наблюдением
-ом
шаге располагает наблюдением![]() ,
образованным первыми
,
образованным первыми![]() случайными величинами последовательности
(при
случайными величинами последовательности
(при![]() наблюдения нет), на основе которого
принимает в точности одно из следующих
решений:
наблюдения нет), на основе которого
принимает в точности одно из следующих
решений:
остановиться и принять
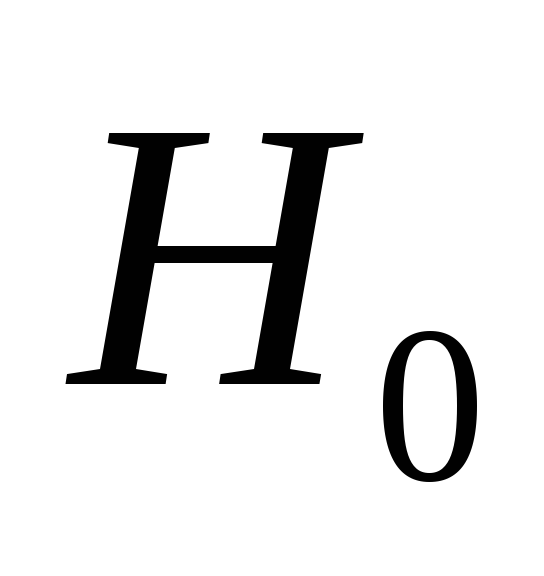 ;
;продолжить и перейти к наблюдению
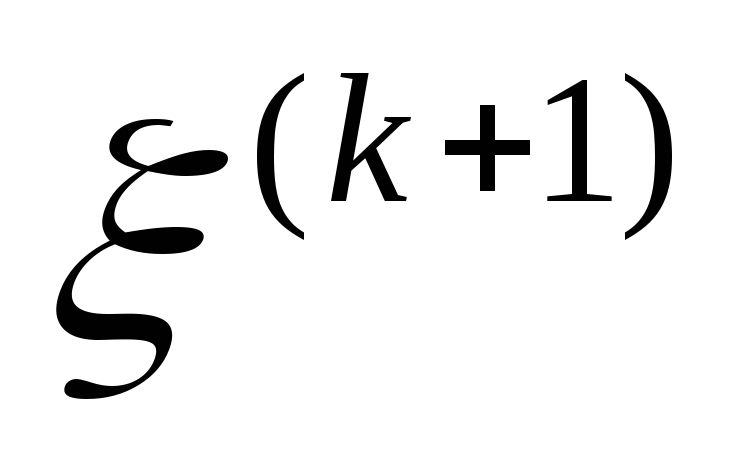 ;
;остановиться и принять
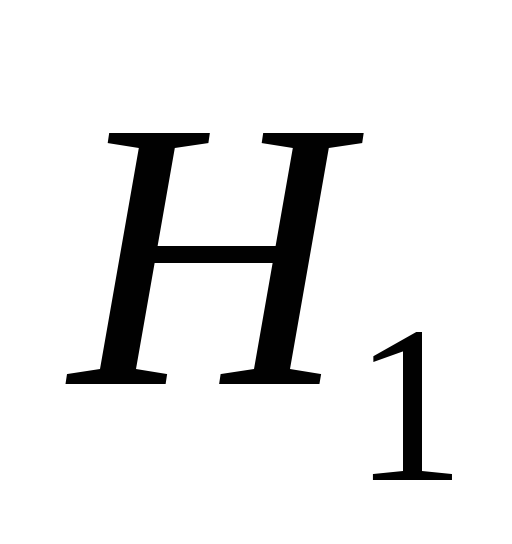 .
.
Пусть множество
![]() есть множество всех возможных реализаций
есть множество всех возможных реализаций![]() последовательности
последовательности![]() :
:
![]() .
.
Для каждого
![]() определим множества
определим множества![]() и
и![]() :
пусть
:
пусть![]() – множество таких последовательностей
– множество таких последовательностей![]() ,
для которых критерий
,
для которых критерий![]() выбрал остановку на шаге
выбрал остановку на шаге![]() и принял гипотезу
и принял гипотезу![]() ,
а множество
,
а множество![]() – множество таких последовательностей
– множество таких последовательностей![]() ,
для которых критерий
,
для которых критерий![]() выбрал остановку на шаге
выбрал остановку на шаге![]() и принял гипотезу
и принял гипотезу![]() .
.
Вполне очевидно, что при фиксированном
![]() :
:
![]() ,
,
поскольку критерий не может одновременно
принять и
![]() и
и![]() .
Кроме того для любых
.
Кроме того для любых![]() и
и![]() ,
,![]() :
:
![]() ,
,
![]() ,
,
поскольку критерий не может для одной
и той же последовательности
![]() одновременно остановится на шаге
одновременно остановится на шаге![]() и на шаге
и на шаге![]() ,
если остановка произошла на шаге
,
если остановка произошла на шаге![]() ,
то шага
,
то шага![]() вовсе не будет.
вовсе не будет.
Каждому последовательному критерию
![]() соответствуют конечные или счетные
совокупности множеств
соответствуют конечные или счетные
совокупности множеств![]() и
и![]() ,
и наоборот, задание двух совокупностей
,
и наоборот, задание двух совокупностей![]() и
и![]() однозначно определяет некоторый
последовательный критерий
однозначно определяет некоторый
последовательный критерий![]() ,
поэтому в дальнейшем будем использовать
обозначение
,
поэтому в дальнейшем будем использовать
обозначение![]() .
.
В соответствии с определением множеств
![]() и
и![]() ,
множество
,
множество![]() есть множество последовательностей
есть множество последовательностей![]() ,
при которых критерий
,
при которых критерий![]() останавливается и принимает гипотезу
останавливается и принимает гипотезу![]() ,
множество
,
множество![]() есть множество последовательностей
есть множество последовательностей![]() ,
при которых критерий
,
при которых критерий![]() останавливается и принимает гипотезу
останавливается и принимает гипотезу![]() .
Очевидно, что
.
Очевидно, что![]() ,
но не обязательно
,
но не обязательно![]() .
.
В случае, когда
![]() для всякой последовательности
для всякой последовательности![]() критерий
критерий![]() никогда не останавливается (на каждом
шаге критерий
никогда не останавливается (на каждом
шаге критерий![]() принимает решение продолжить и получить
следующее наблюдение). К сожалению,
такие критерии тоже попадают в класс
последовательных критериев, поэтому
при формулировке последовательного
критерия следует отдельно рассматривать
вопрос об остановке критерия за конечное
число шагов.
принимает решение продолжить и получить
следующее наблюдение). К сожалению,
такие критерии тоже попадают в класс
последовательных критериев, поэтому
при формулировке последовательного
критерия следует отдельно рассматривать
вопрос об остановке критерия за конечное
число шагов.
Согласно определению вероятность ошибки
первого рода критерия – это вероятность
принять гипотезу
![]() в случае, когда верна гипотеза
в случае, когда верна гипотеза![]() .
Последовательный критерий принимает
гипотезу
.
Последовательный критерий принимает
гипотезу![]() ,
когда
,
когда![]() ,
а если верна гипотеза
,
а если верна гипотеза![]() ,
то
,
то![]() ,
поэтому вероятность ошибки первого
рода критерия
,
поэтому вероятность ошибки первого
рода критерия![]() :
:
![]() ,
,![]() .
.
где вероятность вычисляется при значении
![]() .
.
Вероятность ошибки второго рода – это
вероятность принять гипотезу
![]() в случае, когда верна гипотеза
в случае, когда верна гипотеза![]() .
Последовательный критерий принимает
гипотезу
.
Последовательный критерий принимает
гипотезу![]() ,
когда
,
когда![]() ,
а если верна гипотеза
,
а если верна гипотеза![]() ,
то
,
то![]() ,
поэтому вероятность ошибки второго
рода критерия
,
поэтому вероятность ошибки второго
рода критерия![]() :
:
![]() ,
,![]() .
.
Определение 8.12.
Критерий
![]() являетсякритериемсилы
являетсякритериемсилы![]() ,
если:
,
если:
![]() ,
,
![]() .
.
Кроме вероятностей ошибок первого и
второго родов, каждый последовательный
критерий
![]() характеризуется случайной величиной
количества шагов до остановки,
характеризуется случайной величиной
количества шагов до остановки,![]() .
Если для элементарного события
.
Если для элементарного события![]() наблюдение
наблюдение![]() ,
то это означает, что критерий
,
то это означает, что критерий![]() остановился на шаге с номером
остановился на шаге с номером![]() ,
то есть количество шагов
,
то есть количество шагов![]() .
Отсюда следует определение для случайной
величины
.
Отсюда следует определение для случайной
величины![]() :
:
![]() ,
если
,
если![]() .
.
Поскольку для каждого последовательного
критерия
![]() количество шагов до остановки
количество шагов до остановки![]() является величиной случайной, то для
является величиной случайной, то для![]() определена функция распределения
определена функция распределения![]() ,
зависящая от параметра
,
зависящая от параметра![]() ,
и в некоторых случаях определено
математическое ожидание:
,
и в некоторых случаях определено
математическое ожидание:
![]() .
.
Заметим, что при различных значениях
параметра
![]() математические ожидания
математические ожидания![]() и
и![]() могут оказаться различными.
могут оказаться различными.
Пусть
![]() (
(![]() )
и
)
и![]() (
(![]() )
заданные величины вероятностей ошибок
первого и второго родов соответственно,
рассмотрим класс последовательных
критериев силы
)
заданные величины вероятностей ошибок
первого и второго родов соответственно,
рассмотрим класс последовательных
критериев силы![]() ,
с конечными средними количествами шагов
до остановки:
,
с конечными средними количествами шагов
до остановки:
 .
.
В классе
![]() «наилучшим» критерием является критерий
с наименьшими возможными значениями
«наилучшим» критерием является критерий
с наименьшими возможными значениями![]() и
и![]() .
Можно показать, что существует критерий
.
Можно показать, что существует критерий![]() ,
который одновременно минимизирует оба
математических ожидания, то есть для
любого критерия
,
который одновременно минимизирует оба
математических ожидания, то есть для
любого критерия![]() :
:
![]() ,
,
![]() ,
,
и таким образом критерий
![]() является «наилучшим» в классе
является «наилучшим» в классе![]() .
Кроме того, можно показать, что наилучший
критерий
.
Кроме того, можно показать, что наилучший
критерий![]() является последовательным критерием
отношения вероятностей.
является последовательным критерием
отношения вероятностей.
Определение 8.13.
Последовательный критерий
![]() являетсяпоследовательным критерием
отношения вероятностей(ПКОВ), если
являетсяпоследовательным критерием
отношения вероятностей(ПКОВ), если![]() и при всяком
и при всяком![]() :
:
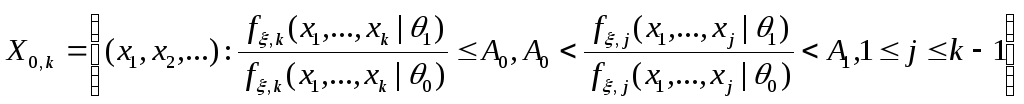 ,
,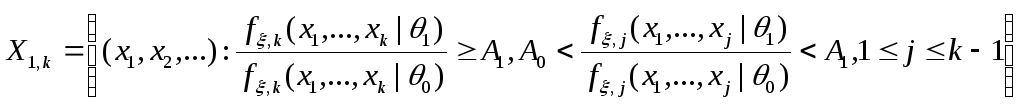 ,
,
где
![]() – функция плотности вероятности функции
распределения
– функция плотности вероятности функции
распределения![]() из условия (C1).
из условия (C1).
Из определения ПКОВ следует:
ПКОВ останавливается на шаге
 и принимает гипотезу
и принимает гипотезу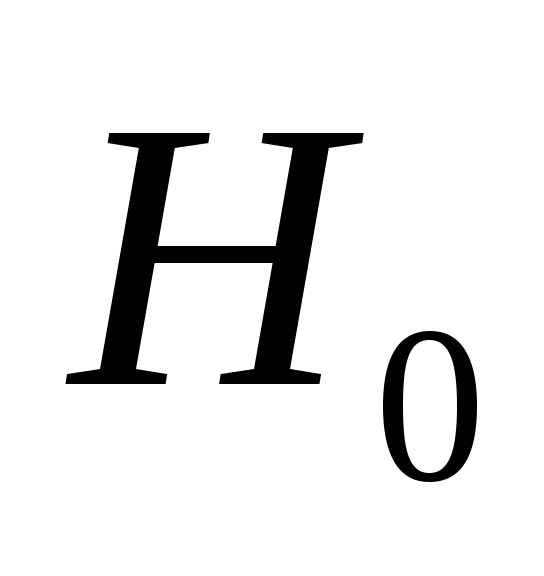 ,
если отношение правдоподобия
,
если отношение правдоподобия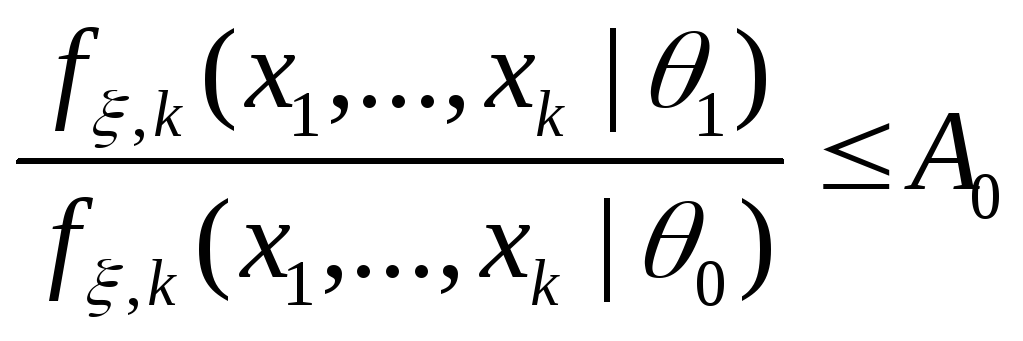 ,
и ПКОВ не остановился ранее, то есть
для всех
,
и ПКОВ не остановился ранее, то есть
для всех (
(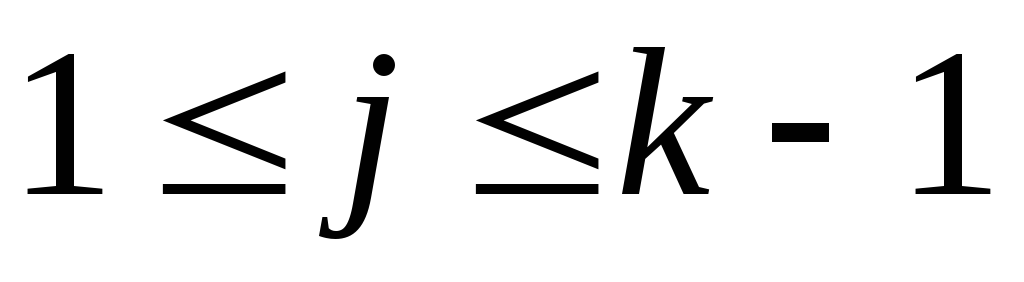 ):
):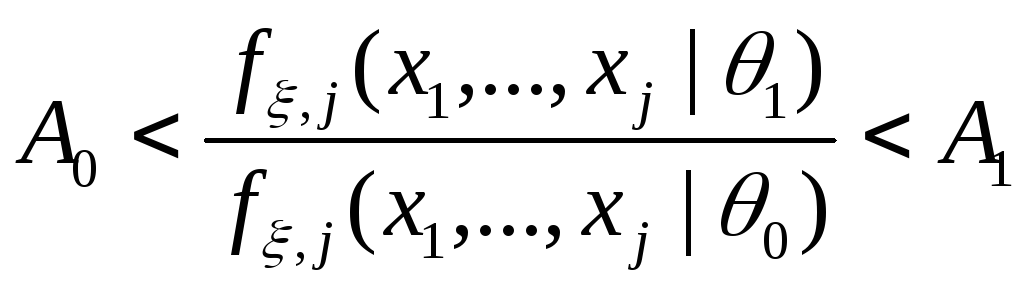 .
.ПКОВ останавливается на шаге
 и принимает гипотезу
и принимает гипотезу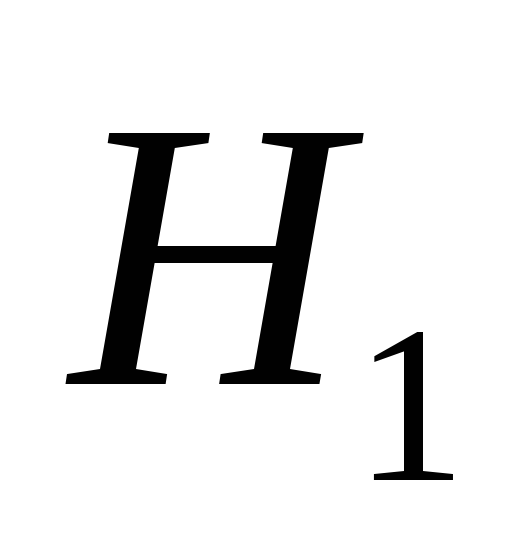 ,
если отношение правдоподобия
,
если отношение правдоподобия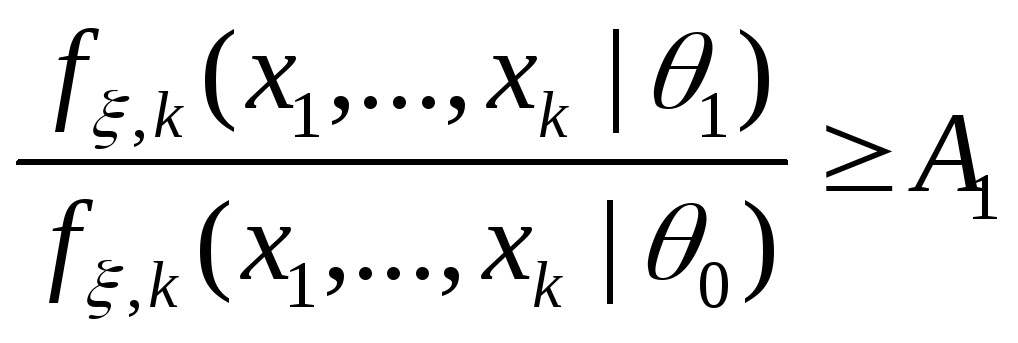 ,
и ПКОВ не остановился ранее, то есть
для всех
,
и ПКОВ не остановился ранее, то есть
для всех (
(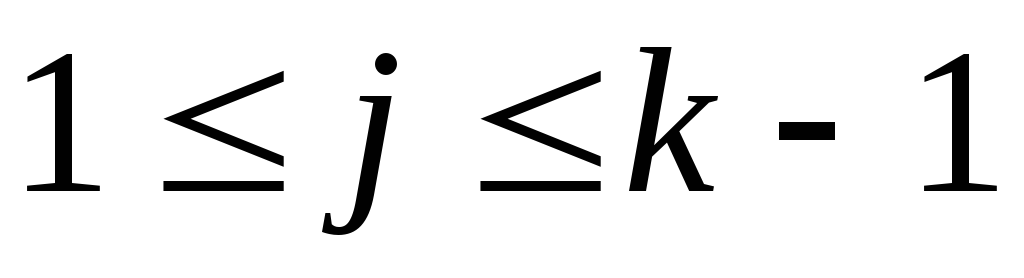 ):
):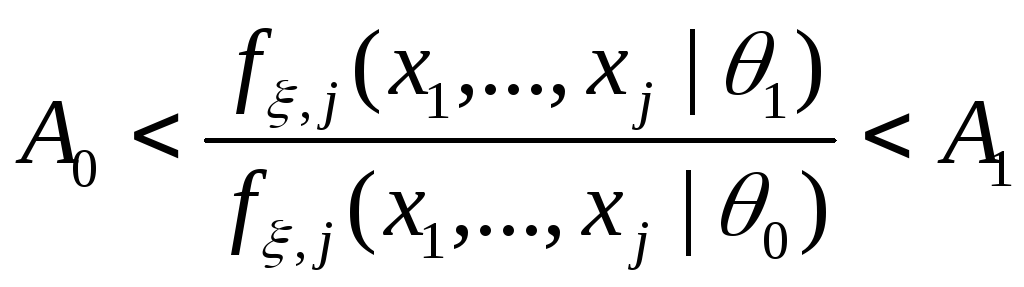 .
.ПКОВ не останавливается и получает следующее наблюдение, если отношение
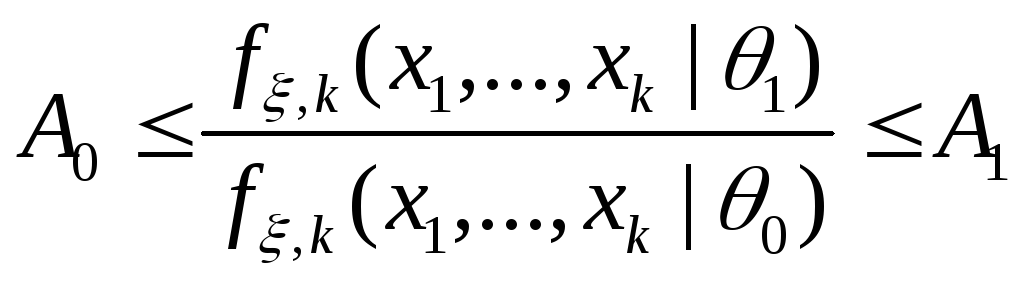 .
.
Рассмотрим первые два шага ПКОВ: на
первом шаге (![]() )
ПКОВ анализирует первое число из
последовательности
)
ПКОВ анализирует первое число из
последовательности![]() ,
сравнивает величину
,
сравнивает величину![]() с заданными значениями
с заданными значениями![]() и
и![]() :
:
если
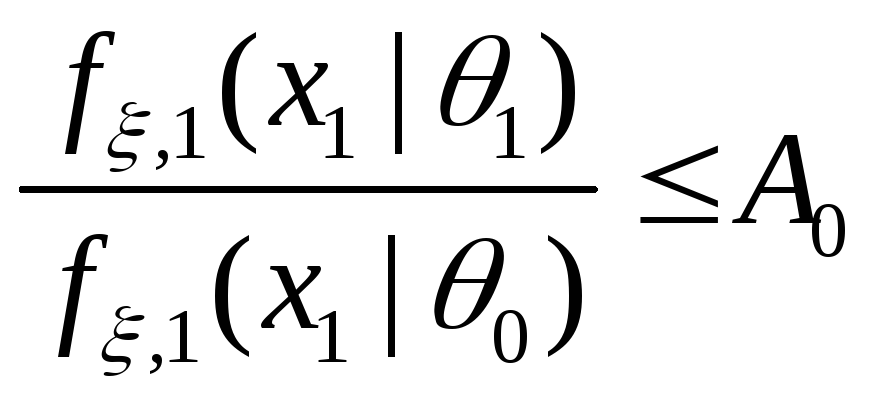 ,
то ПКОВ останавливается и принимает
гипотезу
,
то ПКОВ останавливается и принимает
гипотезу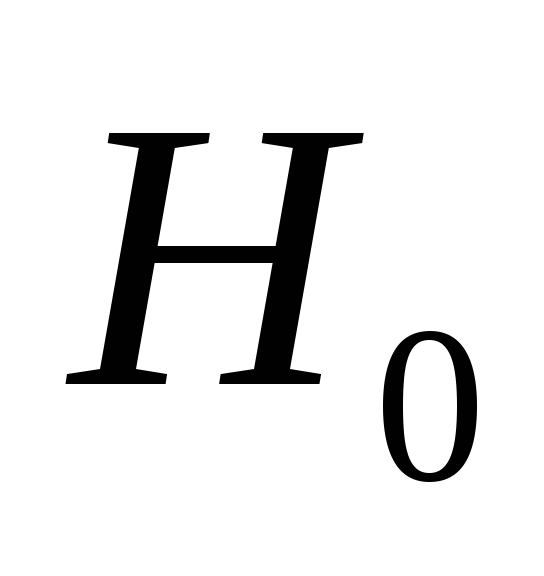 ;
;если
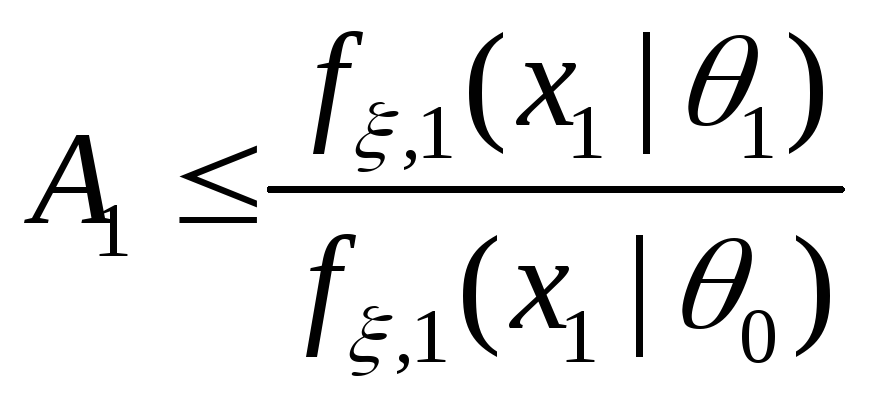 ,
то ПКОВ останавливается и принимает
гипотезу
,
то ПКОВ останавливается и принимает
гипотезу ;
;если
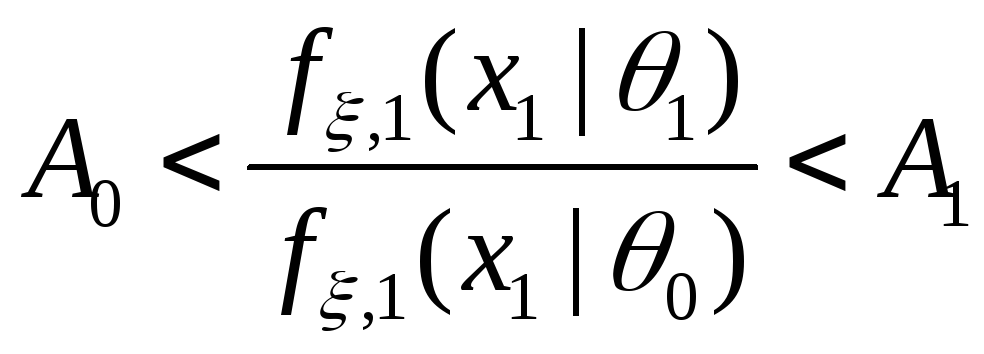 ,
то ПКОВ не останавливается, получает
следующее наблюдение
,
то ПКОВ не останавливается, получает
следующее наблюдение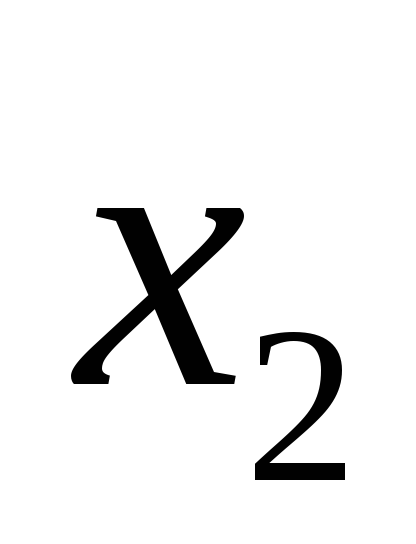 и переходит ко второму шагу.
и переходит ко второму шагу.
На втором шаге (![]() )
ПКОВ анализирует первые два числа из
последовательности
)
ПКОВ анализирует первые два числа из
последовательности![]() ,
сравнивает величину
,
сравнивает величину![]() с заданными значениями
с заданными значениями![]() и
и![]() :
:
если
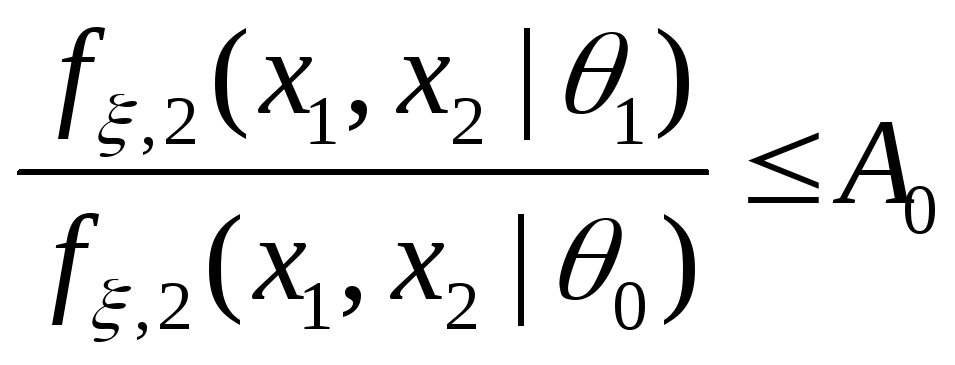 ,
то ПКОВ останавливается и принимает
гипотезу
,
то ПКОВ останавливается и принимает
гипотезу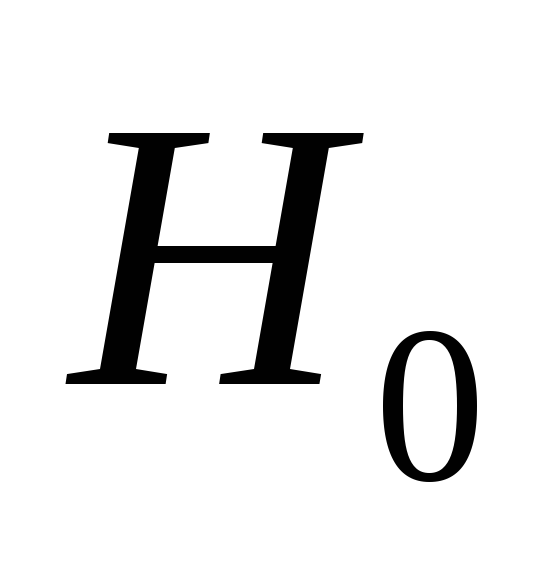 ;
;если
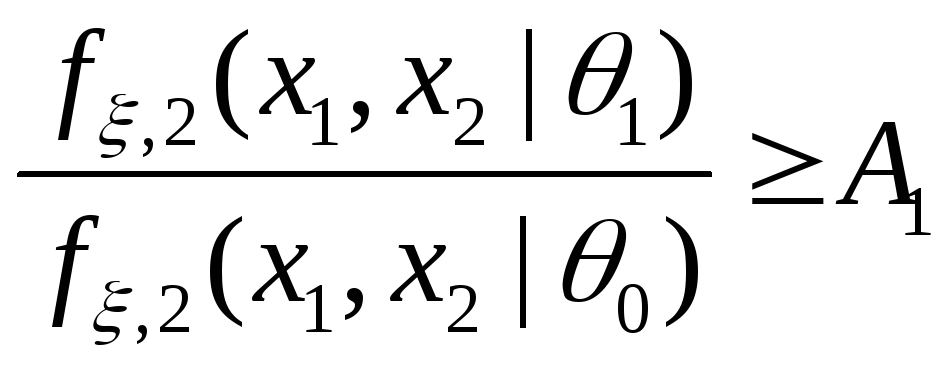 ,
то ПКОВ останавливается и принимает
гипотезу
,
то ПКОВ останавливается и принимает
гипотезу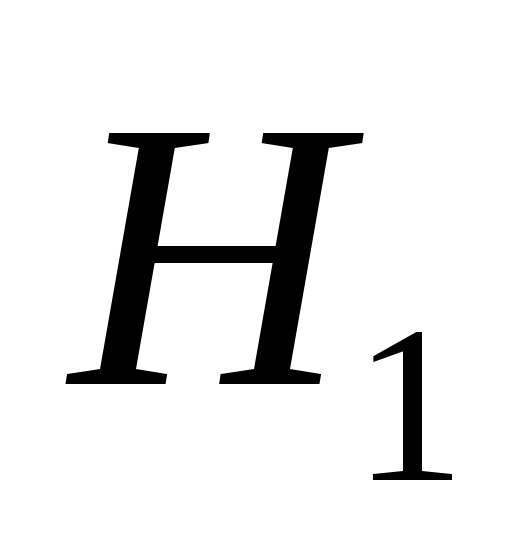 ;
;если
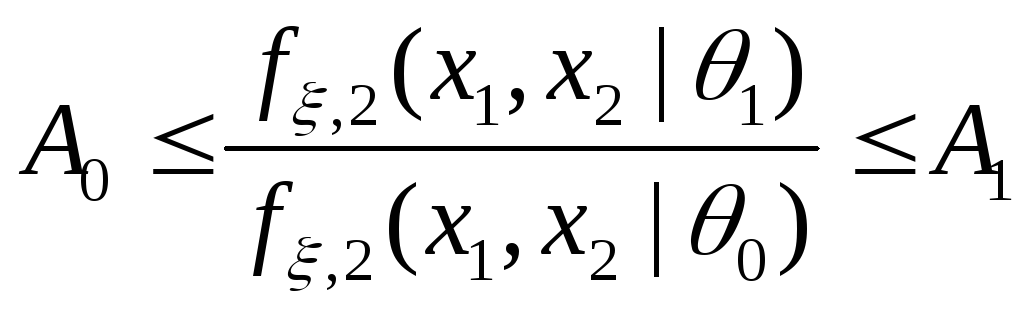 ,
то ПКОВ продолжается, получает следующее
наблюдение
,
то ПКОВ продолжается, получает следующее
наблюдение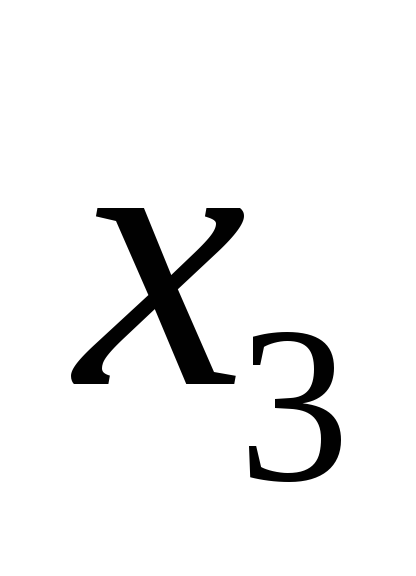 и переходит к третьему шагу.
и переходит к третьему шагу.
Таким образом, ПКОВ на каждом шаге
вычисляет отношение правдоподобия
![]() и как только вычисленное значение
окажется меньше или равно
и как только вычисленное значение
окажется меньше или равно![]() или больше или равно
или больше или равно![]() ,
то ПКОВ сразу же останавливается и
принимает соответствующую гипотезу.
,
то ПКОВ сразу же останавливается и
принимает соответствующую гипотезу.
Рисунок 8.1. Реализация отношения правдоподобия.
Примечательно, что минимальность
математических ожиданий
![]() и
и![]() обеспечивается способом построения
ПКОВ, основанным на сравнении именно
отношения правдоподобия с двумя
пороговыми значениями
обеспечивается способом построения
ПКОВ, основанным на сравнении именно
отношения правдоподобия с двумя
пороговыми значениями![]() и
и![]() ,
в то время как выбор постоянных
,
в то время как выбор постоянных![]() и
и![]() полностью определяет вероятности ошибок
первого
полностью определяет вероятности ошибок
первого![]() и второго
и второго![]() родов критерия. К сожалению, в большинстве
случаев крайне сложно установить точные
выражения, связывающие величины
родов критерия. К сожалению, в большинстве
случаев крайне сложно установить точные
выражения, связывающие величины![]() и
и![]() ПКОВ с вероятностями ошибок
ПКОВ с вероятностями ошибок![]() и
и![]() .
Тем не менее, для некоторых ПКОВ удается
установить оценки снизу и сверху для
постоянных
.
Тем не менее, для некоторых ПКОВ удается
установить оценки снизу и сверху для
постоянных![]() и
и![]() ,
в которых фигурируют вероятности ошибок
,
в которых фигурируют вероятности ошибок![]() и
и![]() .
.
Утверждение 8.14.
Пусть для последовательности случайных
величин
![]() функции распределения
функции распределения![]() первых
первых![]() величин последовательности удовлетворяют
условиям (C1) и (C2).
Пусть ПКОВ
величин последовательности удовлетворяют
условиям (C1) и (C2).
Пусть ПКОВ![]() с вероятностью 1 останавливается за
конечное число шагов, тогда:
с вероятностью 1 останавливается за
конечное число шагов, тогда:
![]() ,
,![]() .
.
Доказательство:
1) Пусть ПКОВ
![]() ,
тогда множество
,
тогда множество![]() есть множество тех последовательностей
есть множество тех последовательностей![]() ,
при которых ПКОВ
,
при которых ПКОВ![]() останавливается за конечное число
шагов. Действительно, если для заданной
последовательности
останавливается за конечное число
шагов. Действительно, если для заданной
последовательности![]() ПКОВ
ПКОВ![]() останавливается на некотором конечном
шаге
останавливается на некотором конечном
шаге![]() ,
то
,
то![]() и тогда
и тогда![]() .
.
Множество
![]() есть множество тех последовательностей
есть множество тех последовательностей![]() для которых ПКОВ
для которых ПКОВ![]() никогда не останавливается. Легко
видеть, что
никогда не останавливается. Легко
видеть, что![]() и множества
и множества![]() ,
тогда:
,
тогда:
![]() .
.
По условию утверждения ПКОВ
![]() останавливается за конечное число шагов
с вероятностью 1, это по определению
означает, что
останавливается за конечное число шагов
с вероятностью 1, это по определению
означает, что![]() ,
тогда:
,
тогда:
![]() .
.
Легко видеть, что
![]() ,
поэтому:
,
поэтому:
![]() .
.
Поскольку множества
![]() и
и![]() попарно не пересекаются, то
попарно не пересекаются, то![]() ,
и следовательно:
,
и следовательно:
![]() ,
,
|
|
(8.6а) |
Поскольку множества
![]() попарно не пересекаются, то в силу
счетно-аддитивности меры
попарно не пересекаются, то в силу
счетно-аддитивности меры![]() :
:
|
|
(8.6б) |
Множества
![]() также попарно не пересекаются, поэтому
в силу счетно-аддитивности меры
также попарно не пересекаются, поэтому
в силу счетно-аддитивности меры![]() :
:
|
|
(8.6в) |
Из (8.6а), (8.6б) и (8.6в) следует, что:
|
|
(8.7) |
2) Заметим, что вероятности ошибок первого
и второго родов критерия
![]() из (8.6в) и (8.6б):
из (8.6в) и (8.6б):
|
|
(8.8) |
3) Согласно (8.8):
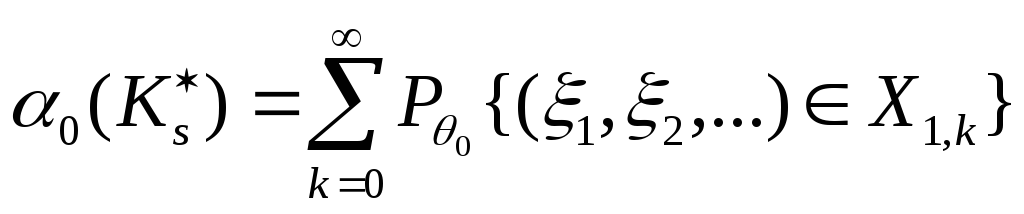 ,
,
причем из условия (C1) следует, что:
![]() .
.
Для всех
![]() :
:
![]()
![]() ,
,
тогда,
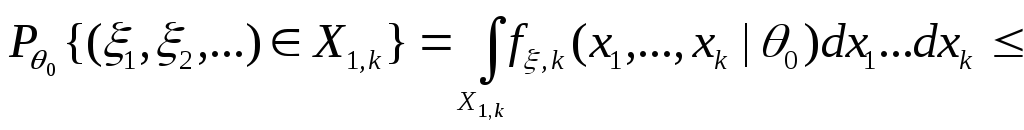
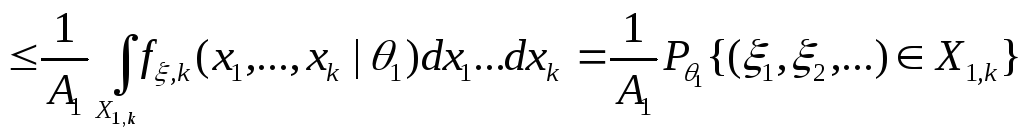 ,
,
откуда с учетом (8.7) и (8.8):
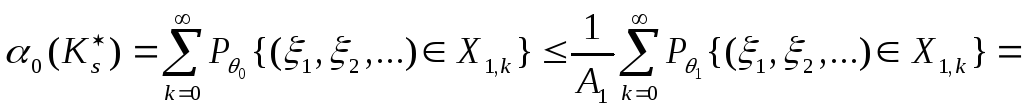
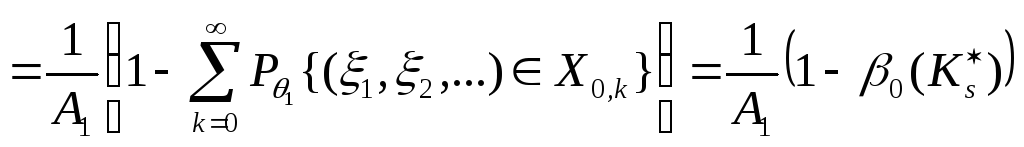 ,
,
![]() ,
,
![]() .
.
5) Аналогично, согласно (8.8):
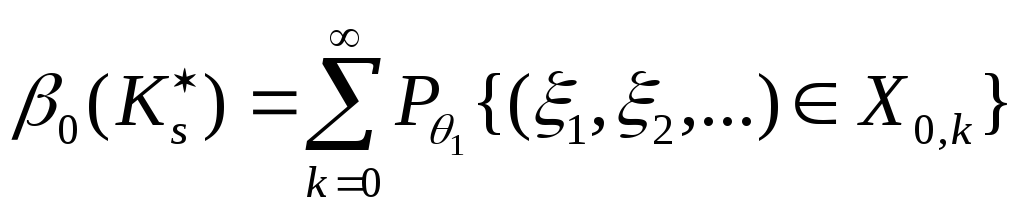 ,
,
причем, из условия (C1) следует, что:
 .
.
Для всех
![]() :
:
![]() ,
,
![]() ,
,
тогда,
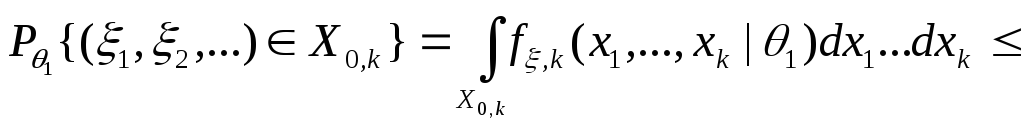
 .
.
Откуда в силу (8.7) и (8.8):
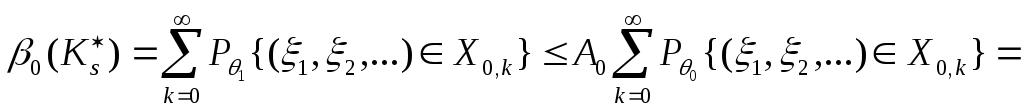
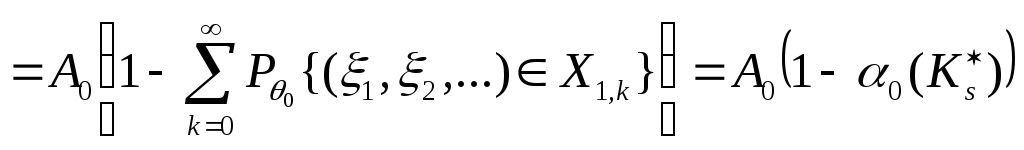 .
.
![]() ,
,
![]() .
.
Утверждение доказано.
Предположим, требуется построить ПКОВ
заданной силы
![]() (определение8.12),
где
(определение8.12),
где![]() .
Величины
.
Величины![]() и
и![]() определяют постоянные
определяют постоянные![]() и
и![]() ПКОВ
ПКОВ![]() ,
однако выражения для них неизвестны, и
построить ПКОВ
,
однако выражения для них неизвестны, и
построить ПКОВ![]() с вероятностями ошибок точно равными
с вероятностями ошибок точно равными![]() и
и![]() не представляется возможным. Тем не
менее, из утверждения 8.14 известны оценки
для
не представляется возможным. Тем не
менее, из утверждения 8.14 известны оценки
для![]() и
и![]() ,
воспользовавшись которыми можно
построить ПКОВ
,
воспользовавшись которыми можно
построить ПКОВ![]() .
Конечно вероятности ошибок
.
Конечно вероятности ошибок
![]() и
и![]() критерия
критерия![]() в общем случае не совпадают с заданными
в общем случае не совпадают с заданными![]() и
и![]() ,
тем не менее, можно надеется, что эти
величины будут различаться несущественно.
,
тем не менее, можно надеется, что эти
величины будут различаться несущественно.
Утверждение 8.15.
Пусть для последовательности
![]() случайных величин функции распределения
случайных величин функции распределения![]() первых
первых![]() величин последовательности удовлетворяют
условиям (C1) и (C2).
Пусть заданы числа
величин последовательности удовлетворяют
условиям (C1) и (C2).
Пусть заданы числа![]() и
и![]() ,
,![]() и
и![]() ,
и известно, что ПКОВ
,
и известно, что ПКОВ![]() с вероятностью 1 останавливается за
конечное число шагов,
с вероятностью 1 останавливается за
конечное число шагов,![]() и
и![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
![]() .
.
Доказательство:
В условиях утверждения справедливо
утверждение 8.14, согласно которому для
ПКОВ
![]() ,
с
,
с![]() и
и![]() :
:
|
|
(8.9а) |
|
|
(8.9б) |
Из (8.9а) следует:
![]() .
.
Из (8.9б) следует:
![]() ,
,
![]() .
.
Из (8.9а) и (8.9б) следует:
![]() ,
,
![]() .
.
Складывая неравенства, получим:
![]() ,
,
![]() ,
,
![]() .
.
Утверждение доказано.
Заметим, что величины
![]() и
и![]() ,
как правило, очень малы, поэтому
,
как правило, очень малы, поэтому![]() и
и![]() ,
следовательно:
,
следовательно:
![]() ,
,
![]() ,
,
поэтому даже если вероятности ошибок
ПКОВ
![]() превышают заданные значения
превышают заданные значения![]() и
и![]() ,
то не на много. Уменьшенные вероятностей
ошибок ПКОВ
,
то не на много. Уменьшенные вероятностей
ошибок ПКОВ![]() по сравнению с заданными
по сравнению с заданными![]() и
и![]() совершенно точно не уменьшают средние
количества шагов до остановки, то есть
у ПКОВ
совершенно точно не уменьшают средние
количества шагов до остановки, то есть
у ПКОВ![]() математические ожидания количества
шагов до остановки
математические ожидания количества
шагов до остановки![]() скорее всего окажутся больше аналогичных
математических ожиданий
скорее всего окажутся больше аналогичных
математических ожиданий![]() ПКОВ
ПКОВ![]() с вероятностями ошибок точно равных
с вероятностями ошибок точно равных![]() и
и![]() .
Причем разница математических ожиданий,
по-видимому, будет тем больше, чем больше
различаются вероятности
.
Причем разница математических ожиданий,
по-видимому, будет тем больше, чем больше
различаются вероятности![]() и
и![]() ,
и вероятности
,
и вероятности![]() и
и![]() .
.
Построение ПКОВ
![]() основано на утверждениях 8.14 и 8.15
справедливых для тех ПКОВ, которые с
вероятностью 1 останавливаются за
конечное число шагов. В общем случае,
задача подсчета вероятности остановки
произвольного ПКОВ за конечное число
шагов может оказаться весьма сложной,
поэтому перейдем к рассмотрению более
простой задачи, введя дополнительное
условие (C3):
основано на утверждениях 8.14 и 8.15
справедливых для тех ПКОВ, которые с
вероятностью 1 останавливаются за
конечное число шагов. В общем случае,
задача подсчета вероятности остановки
произвольного ПКОВ за конечное число
шагов может оказаться весьма сложной,
поэтому перейдем к рассмотрению более
простой задачи, введя дополнительное
условие (C3):
(C3) Пусть при всех![]() и
и![]() :
:
![]() .
.
Другими словами условие (C3)
означает, что в последовательности
случайных величин![]() все величины имеют одинаковую плотность
вероятности
все величины имеют одинаковую плотность
вероятности![]() и любая конечная совокупность величин
является совместно независимой.
и любая конечная совокупность величин
является совместно независимой.
В условиях (С1), (С2) и (С3) отношение
правдоподобия на шаге
![]() принимает вид:
принимает вид:
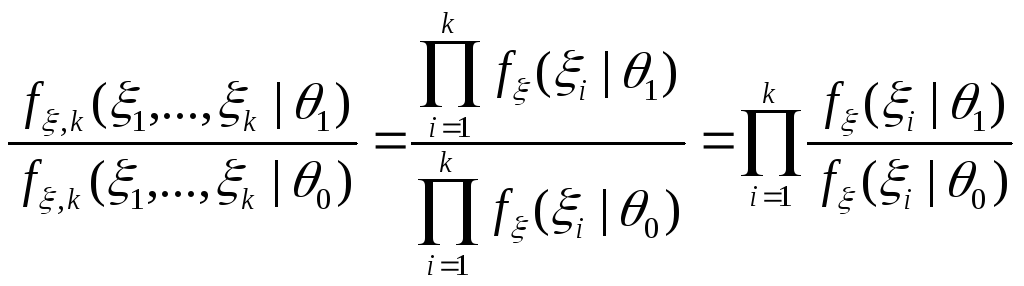 ,
,
тогда условие продолжения на шаге
![]() ПКОВ
ПКОВ![]() имеет вид:
имеет вид:
![]() .
.
Поскольку все величины в неравенстве положительные, то вычисляя логарифм от всех частей, получим неравенство:
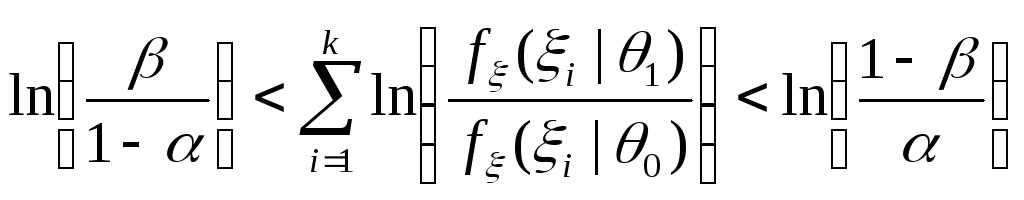 .
.
Утверждение 8.16.
Пусть для последовательности случайных
величин
![]() функции распределения
функции распределения![]() первых
первых![]() величин последовательности удовлетворяют
условиям (C1), (C2)
и (C3), причем дисперсии
величин последовательности удовлетворяют
условиям (C1), (C2)
и (C3), причем дисперсии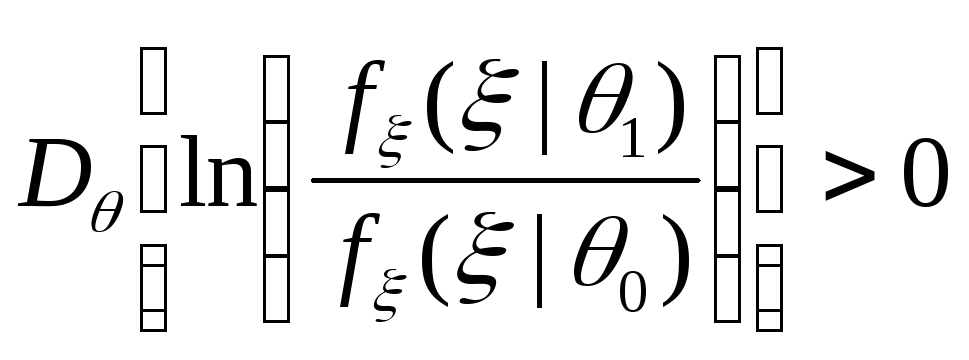 ,
где
,
где![]() – случайная величина с плотностью
вероятности
– случайная величина с плотностью
вероятности![]() (
(![]() ).
).
Тогда для любых конечных
![]() и
и![]() ПКОВ
ПКОВ![]() с вероятностью 1 останавливается за
конечное число шагов.
с вероятностью 1 останавливается за
конечное число шагов.
Без доказательства.
Следствие
В условиях утверждения 8.16 можно показать,
что все моменты случайной величины
количества шагов до остановки
![]() конечны.
конечны.
Среди всех последовательных критериев
заданной силы
![]() ПКОВ
ПКОВ![]() силы
силы![]() имеет наименьшие возможные значения
математических ожиданий
имеет наименьшие возможные значения
математических ожиданий![]() (
(![]() ).
Вычисление величин
).
Вычисление величин![]() в общем случае представляет сложную
задачу, тем не менее, в некоторых случаях
может быть получено простое приближенное
выражение.
в общем случае представляет сложную
задачу, тем не менее, в некоторых случаях
может быть получено простое приближенное
выражение.
Утверждение 8.17. (тождество Вальда)
Пусть в последовательности случайных
величин
![]() все случайные величины имеют одинаковое
распределение и конечное математическое
ожидание
все случайные величины имеют одинаковое
распределение и конечное математическое
ожидание![]() ,
случайная величина
,
случайная величина![]() принимает значения из множества
натуральных чисел, имеет конечное
математическое ожидание
принимает значения из множества
натуральных чисел, имеет конечное
математическое ожидание![]() ,
и при любом натуральном
,
и при любом натуральном![]() событие
событие![]() зависит только от случайных величин
зависит только от случайных величин![]() ,
..,
,
..,![]() .
Тогда случайная величина
.
Тогда случайная величина![]() :
:
![]()
имеет математическое ожидание
![]() :
:
![]() .
.
Если дополнительно для всех
![]()
![]() ,
тогда:
,
тогда:
![]() .
.
Без доказательства.
В момент остановки критерия
![]() шаг
шаг![]() равен случайной величине
равен случайной величине![]() ,
поэтому случайная величина
,
поэтому случайная величина![]() :
:
|
|
(8.10) |
является значением отношения правдоподобия
в момент остановки критерия
![]() .
Если существует
.
Если существует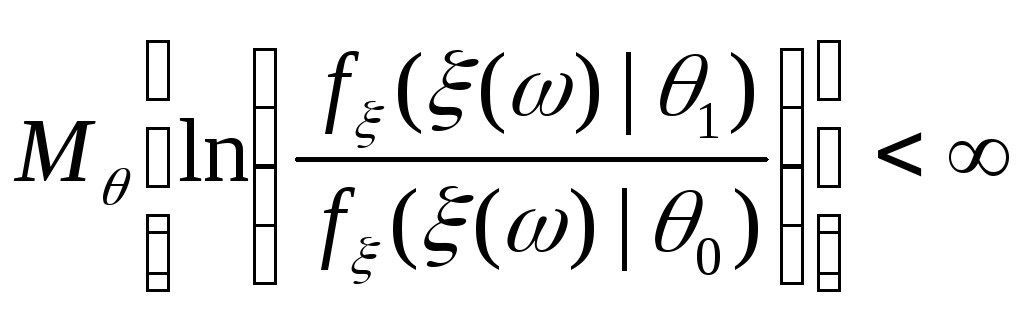 ,
тогда к последовательности случайных
величин
,
тогда к последовательности случайных
величин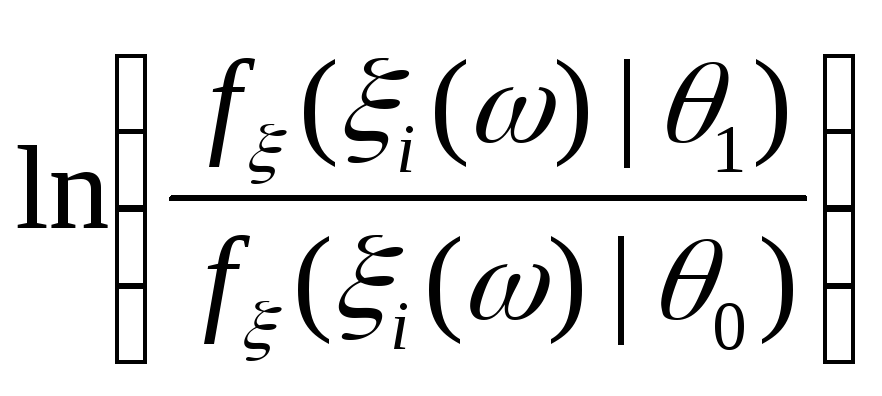 и случайной величине
и случайной величине![]() применимо утверждение 8.17 (тождество
Вальда), откуда следует, что:
применимо утверждение 8.17 (тождество
Вальда), откуда следует, что:
|
|
(8.11) |
где
![]() является случайной величиной с плотностью
вероятности
является случайной величиной с плотностью
вероятности![]() .
.
Поскольку величины
![]() и
и![]() как правило малы, то диапазон между
пороговыми значениями
как правило малы, то диапазон между
пороговыми значениями![]() и
и![]() оказывается очень широким, если при
этом отдельные слагаемые
оказывается очень широким, если при
этом отдельные слагаемые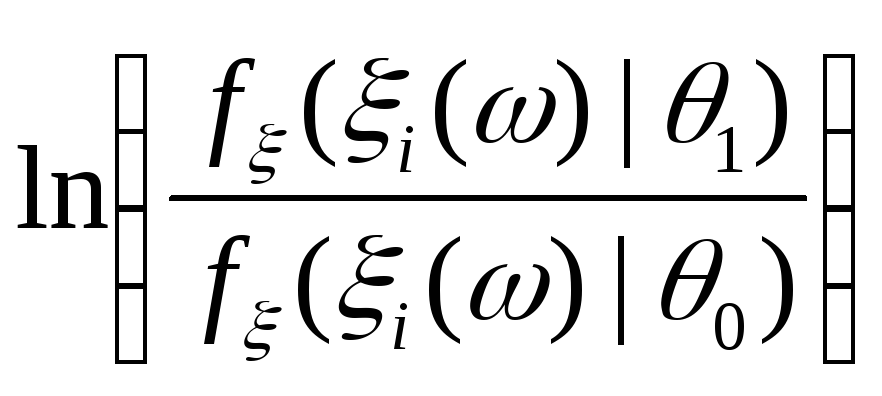 в сумме оказываются с большой вероятностью
небольшими величинами, то в момент
выхода суммы
в сумме оказываются с большой вероятностью
небольшими величинами, то в момент
выхода суммы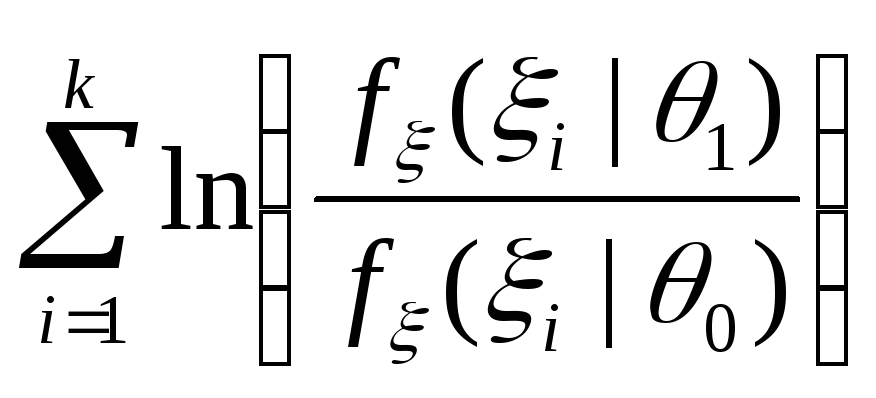 из интервала
из интервала![]() ,
образованного пороговыми значениями,
значение суммы (8.10) незначительно
отличается от самого порогового значения.
В частности если математические ожидания
и дисперсии случайной величины
,
образованного пороговыми значениями,
значение суммы (8.10) незначительно
отличается от самого порогового значения.
В частности если математические ожидания
и дисперсии случайной величины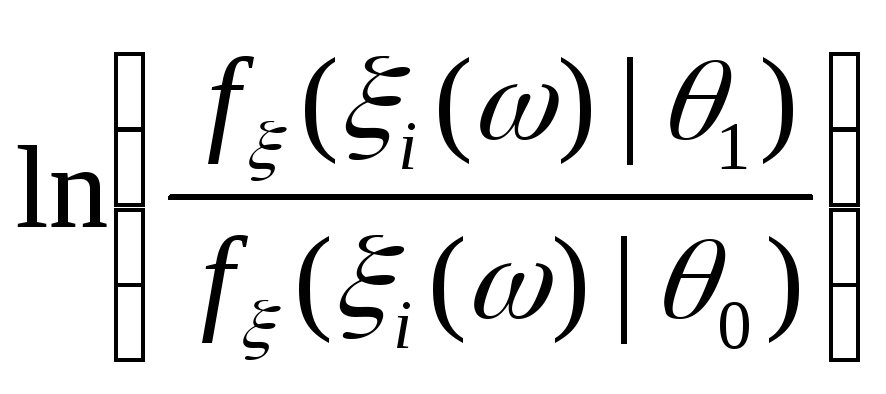 (где
(где![]() имеет плотность вероятности
имеет плотность вероятности![]() либо
либо![]() )
оказываются малыми величинами, то в
момент остановки отношение правдоподобия
примерно совпадает с пороговыми
значениями:
)
оказываются малыми величинами, то в
момент остановки отношение правдоподобия
примерно совпадает с пороговыми
значениями:
![]() ,
если принимается
,
если принимается![]() ,
,
![]() ,
если принимается
,
если принимается![]() .
.
Пусть
![]() – множество последовательностей, для
которых критерий
– множество последовательностей, для
которых критерий![]() останавливается и принимает гипотезу
останавливается и принимает гипотезу![]() ,
а множество
,
а множество![]() – множество последовательностей, для
которых критерий
– множество последовательностей, для
которых критерий![]() останавливается и принимает гипотезу
останавливается и принимает гипотезу![]() .
.
Если верна гипотеза
![]() ,
то есть
,
то есть![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
где
![]() есть вероятность ошибки первого рода
критерия
есть вероятность ошибки первого рода
критерия![]() ,
которая приближенно равна
,
которая приближенно равна![]() ,
тогда:
,
тогда:
|
|
(8.12а) |
Приравнивая правые части (8.11) и (8.12а) получим:
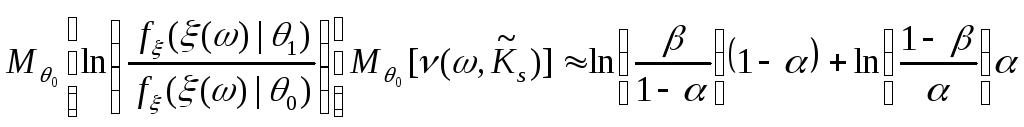 ,
,
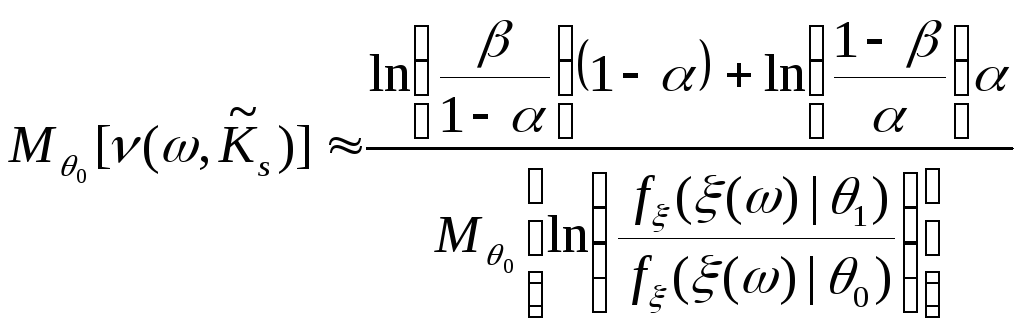 ,
,
где
![]() – случайная величина, имеющая плотность
вероятности
– случайная величина, имеющая плотность
вероятности![]() .
.
Аналогично, если верна гипотеза
![]() ,
то
,
то![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
где
![]() есть вероятность ошибки второго рода
критерия
есть вероятность ошибки второго рода
критерия![]() ,
которая приближенно равна
,
которая приближенно равна![]() ,
тогда:
,
тогда:
|
|
(8.12б) |
Приравнивая правые части (8.11) и (8.12б) получим:
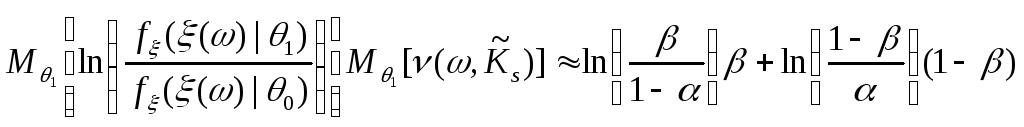 ,
,
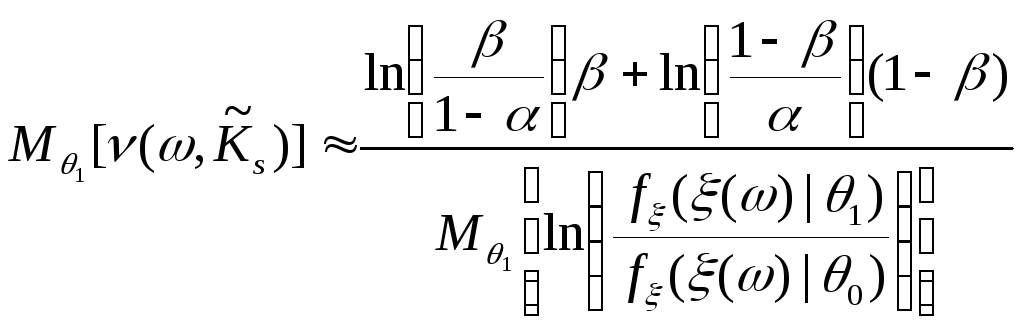 ,
,
где
![]() – случайная величина, имеющая плотность
вероятности
– случайная величина, имеющая плотность
вероятности![]() .
.
|
|
|

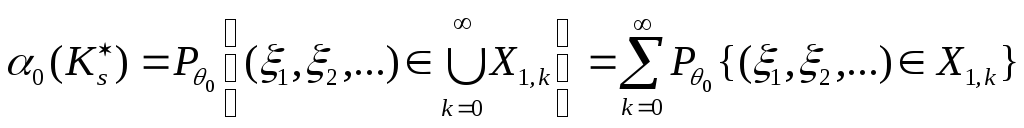 ,
,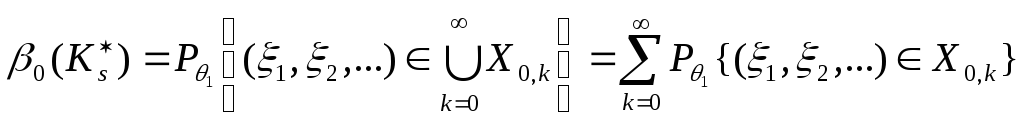 .
.