- •Классификация систем автоматического управления, принципы управления.
- •Уравнения звеньев.
- •Линеаризация уравнений динамики звеньев.
- •Передаточные функции и временные характеристики звеньев.
- •Частотные характеристики звеньев.
- •Элементарные звенья: идеальное интегрирующее звено.
- •Элементарные звенья: идеальное дифференцирующее звено.
- •Элементарные звенья: апериодическое звено первого порядка.
- •Элементарные звенья: колебательное звено.
- •Элементарные звенья: форсующее звено первого порядка.
- •Особенности и физическая реализация звеньев.
- •Структурные схемы и структурные преобразования.
- •Частотные характеристики систем.
- •Общие описания процессов.
- •Понятие устойчивости линейных систем.
- •Алгебраические критерии Гурвица.
- •Критерии устойчивости Михайлова.
- •Критерии устойчивости Найквиста.
- •Понятие точности. Постоянные ошибки.
- •Установившаяся ошибка при производном сигнале.
- •Установившаяся ошибка при гармоническом сигнале.
- •Корневые оценки качества.
- •Интегральные оценки качества.
- •Частотные оценки качества.
- •Описание систем управления с помощью уравнений состояния.
- •Последовательные корректирующие устройства.
- •Параллельные корректирующие устройства.
- •Корректирующие устройства по внешнему воздействию.
- •Описание разомкнутых импульсных систем.
- •Частотные характеристики импульсных систем.
- •Характеристики замкнутых импульсных систем.
- •Устойчивость процессов в импульсных системах.
- •Точность импульсных систем.
- •Оценки качества импульсных систем.
Описание разомкнутых импульсных систем.
Структура разомкнутой импульсной системы приведена на рис. 1.4.
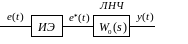
Рис. 1.4
Линейная непрерывная
часть системы характеризуется передаточной
функцией
 ,
а импульсный элемент законом модуляции
,
а импульсный элемент законом модуляции
 и постоянными значениями величин
и постоянными значениями величин
 и
и
 .
Заметим, что сигналы
.
Заметим, что сигналы
 и
и
 непрерывные, а
непрерывные, а
 последовательность
прямоугольных импульсов, модулированных
по амплитуде.
последовательность
прямоугольных импульсов, модулированных
по амплитуде.
Рассмотрим получение
разностного уравнения на простейшем
примере. Пусть
 ,
тогда
и
связаны дифференциальным уравнением
,
тогда
и
связаны дифференциальным уравнением
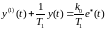 ,
которое легко решается.
,
которое легко решается.
Обозначим значение
координаты
в произвольный момент времени квантования
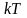 через
через
 ,
тогда на интервале действия
,
тогда на интервале действия
 -ого
импульса
-ого
импульса
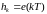 и закон изменения выхода будет
и закон изменения выхода будет
 ,
,
 . (1.12)
. (1.12)
Найдем закон изменения
на интервале паузы в
 -ом
периоде, когда
-ом
периоде, когда
 .
Он будет иметь вид
.
Он будет иметь вид
 .
(1.13)
.
(1.13)
Полагая в (1.12)
 ,
найдем
,
найдем
 ,
подставим в (1.13) и после преобразований
будем иметь
,
подставим в (1.13) и после преобразований
будем иметь
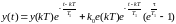 ,
,
 . (1.14)
. (1.14)
Положим в (1.14)
 и, обозначая
и, обозначая
 ,
,
 ,
,
 будем иметь
будем иметь
 ,
(1.15)
,
(1.15)
где
 ,
,
 .
.
Итак, связь
 и
в дискретные моменты времени
описывается линейным разностным
уравнением первого порядка (частный
случай (1.6)), коэффициенты которого
и
в дискретные моменты времени
описывается линейным разностным
уравнением первого порядка (частный
случай (1.6)), коэффициенты которого
 и
и
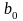 определены через параметры ИЭ и ЛНЧ.
определены через параметры ИЭ и ЛНЧ.
Аналогично, можно
получить разностное уравнение при
 ,
т.е. для смещенных решетчатых функций
,
т.е. для смещенных решетчатых функций
 .
.
Применяя к (1.15)
 преобразование,
найдем для данного случая передаточную
функцию
преобразование,
найдем для данного случая передаточную
функцию

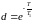 ,
, . (1.16)
. (1.16)
Для простейших случаев передаточных функций можно по этой методике получить дискретные передаточные функции разомкнутой системы. Ниже приведем таблицу для трех вариантов передаточной функции .
Таблица 1.2
|
|
|
|
|
|
|
|
Если передаточная
функция
имеет более высокий порядок, но может
быть представлена в виде суммы передаточных
функций
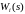 простейшего типа , то в этом случае
находя по табл. 1.2
простейшего типа , то в этом случае
находя по табл. 1.2
 ,
можно получить общую передаточную
функцию разомкнутой системы
,
можно получить общую передаточную
функцию разомкнутой системы
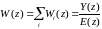 .
.
Рассмотрим другой способ получения передаточной функции разомкнутой системы, излагаемый практически в любом учебнике. Структура на рис. 1.4 может быть представлена в виде, изображенном на рис. 1.5, а.





Рис.1.5
На рис. 1.5, а
импульсный элемент представлен в виде
идеального элемента (ИИЭ) или ключа
и формирующего устройства (ФУ). Ключ
периодически замыкается с периодом
 и формирует последовательность импульсов
в виде
и формирует последовательность импульсов
в виде
 функций,
площадь которых равна
функций,
площадь которых равна
 .
ФУ формирует последовательность
прямоугольных импульсов
,
амплитуда которых равна
.
ФУ формирует последовательность
прямоугольных импульсов
,
амплитуда которых равна
 .
.
По определению функция описывается так:

 .
.
Разумеется, физически
ИИЭ не существует, однако такое
математическое представление ИЭ отражает
физику процессов в исходной структуре
рис.1.3. Объединяя передаточные функции
 и
и
 ,
приходим к структуре рис.1.5, б, где
ЭЛНЧ – эквивалентная линейная
непрерывная часть с передаточной
функцией
,
приходим к структуре рис.1.5, б, где
ЭЛНЧ – эквивалентная линейная
непрерывная часть с передаточной
функцией
 .
В случае прямоугольных импульсов
имеет вид
.
В случае прямоугольных импульсов
имеет вид
 , (1.17)
, (1.17)
где
 .
.
Если
 ,
,
 ,
то такое формирующее устройство называют
фиксатором или экстраполятором
нулевого порядка.
,
то такое формирующее устройство называют
фиксатором или экстраполятором
нулевого порядка.
Если рассматривать
для
 ,
т.е.
и ввести изображения решетчатых функций
,
т.е.
и ввести изображения решетчатых функций
 ,
,
 ,
то связь входа и выхода в области
изображений будет
,
то связь входа и выхода в области
изображений будет
 ,
где передаточную функцию дискретной
разомкнутой системы можно определить
по выражению [6]
,
где передаточную функцию дискретной
разомкнутой системы можно определить
по выражению [6]
 . (1.18)
. (1.18)
Отметим, что
Z–преобразование применяется к решетчатым
функциям. Однако каждой решетчатой
функции
 соответствует непрерывная
,
а ей некоторое изображение
соответствует непрерывная
,
а ей некоторое изображение
 .
Поэтому
.
Поэтому
 будем понимать как символичную запись
будем понимать как символичную запись
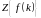 .
.
Алгоритм применения
формулы (1.18) следующий. Если
имеет высокий порядок, то
 представляют в виде суммы простейших
(табличных) слагаемых. Далее по таблицам
представляют в виде суммы простейших
(табличных) слагаемых. Далее по таблицам
 –преобразования
находят изображения каждого слагаемого
и суммируют их. В результате получают
изображение
–преобразования
находят изображения каждого слагаемого
и суммируют их. В результате получают
изображение
 .
Полагая в
.
Полагая в

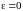 ,
получают первое слагаемое в (1.18) и,
полагая
,
получают первое слагаемое в (1.18) и,
полагая
 ,
– второе.
,
– второе.
Наиболее часто используется случай фиксатора нулевого порядка ( ). В этом случае формула (1.18) упрощается и имеет вид
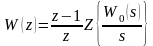 . (1.19)
. (1.19)
В наиболее общем
случае передаточная функция
может быть записана в виде
 .
При этом всегда степень полинома
.
При этом всегда степень полинома
 больше степени полинома
больше степени полинома
 ,
а
,
а
 характеризует порядок астатизма. В этом
случае передаточная функция импульсной
системы будет иметь вид
характеризует порядок астатизма. В этом
случае передаточная функция импульсной
системы будет иметь вид
 , (1.20)
, (1.20)
причем степени
полиномов
 и
и
 будут равны.
будут равны.
Для импульсной системы понятие порядка астатизма сохраняется, т.е. передаточная функция (1.20) соответствует импульсной системе с астатизмом -го порядка.