4.5. Несимметричные автоколебания. Постоянные ошибки

Обратимся к нелинейной системе с внешним воздей­ствием f(t) (рис. 4.27).

Рис.4.27. Нелинейная система

с внешним воздей­ствием f(t)

Уравнение динамики замк­нутой системы будет иметь вид

, (4.57)

где операторный многочлен S(p) зависит от места приложения внешнего воздействия.

Положим правую часть урав­нения (4.57) постоянной:

(4.58)

Это может быть в двух случаях:

1) внешнее воздей­ствие f(t) постоянно: , тогда ;

2) внешнее воздей­ствие f(t) есть линейная функция с постоянной составляющей: , при условии , тогда .

Эти случаи соответственно для систем без астатизма и с астатизмом.

Итак, рассмотрим уравнение системы в виде

(4.59)

В этом случае за счет постоянной правой части уравне­ния появится постоянная составляющая в периодическом решении (несимметричные автоколебания). Поэтому ре­шение ищется в виде (4.15) и (4.16).

Величина характеризует постоянную статическую или скоростную ошибку системы.

Однако несимметричные колебания могут иметь ме­сто и при отсутствии внешнего воздействия, т. е. в си­стеме

(4.60)

если F(x) — несимметричная нелинейность. Это проил­люстрировано на рис. 4.28, где постоянная составляющая F⁰ на выходе нелинейности возникает даже при симмет­ричном входе . Затем постоянная составляющая, вообще говоря, пройдет и на вход х через линей­ную часть системы и приведет к решению вида (4.15) и (4.16). Следовательно, статическая ошибка в нелинейной систе­ме может иметь место и без внешнего воздействия — за счет несимметрии нелинейности.

Гармоническая линеаризация в случае несимметрич­ных колебаний имеет вид (4.16), т. е.

(4.61)

где х⁰ — постоянная составляющая (4.17), q и q' — коэф­фициенты гармонической линеаризации (4.18). Их вы­числение показано в примерах 4.6—4.10 раздела 4.2.

Подставим искомое решение (4.15) и (4.16) в результат

гар­монической линеаризации нелинейности (4.61) в задан­ное уравнение системы (4.59):

Выделим отсюда уравнение для постоянных составляю­щих:

(4.62)

Рис.4.28. Возникновение несимметричных

колебаний

и уравнение для периодических составляющих:

(4.63)

Видно, что постоянная составляющая ( ) и колебатель­ная (α, ω) определяются не в отдельности, а только путем совместного решения этих уравнений.

Сначала из алгебраического уравнений (4.15) и (4.16) можно определить зависимость

(4.64)

Затем подставить эту зависимость в выражения и , имеющиеся для заданной нелинейности. Тог­да получатся новые выражения и графики для q(α) и q'(α), включающие зависимость (4.64). В результате уравнение (4.63) приводится к виду (4.38). Методика решения задачи по определению α и ω остается прежней (раздел 4.3 или раздел 4.4), но с новыми выражениями и графи­ками для q(α) и q'(α).

Определение функции (4.64) упрощает­ся в двух случаях, а именно:

а) при несимметричной нелинейности и без внешнего воздействия вместо (4.62) имеем

;

б) при наличии нулевого полюса в передаточной функции линейной части, когда , вместо (4.62) в общем случае получим

,

а без внешнего воздействия, при несимметричной нели­нейности

Например, при несимметричной нелинейности вида рис. 4.12, а в системе со свойством , со­гласно примеру 4.10 раздела 4.2 получим

Этим определяется зависимость между величиной сме­щения и амплитудой α, после чего используется урав­нение (4.63).

Определение из уравнения (4.63) периодической со­ставляющей х*, т. е. величин α и ω, упрощается в случае однозначной нечетно-симметричной нелинейности . В этом случае, согласно (4.63), характеристическое урав­нение получает вид

(4.64)

а после подстановки аналогично (4.41) придем к уравнениям

Сравнив эти уравнения с (4.41), получаем

, (4.65)

где относится к симметричным автоколебаниям в той же системе, определяемым согласно раздела 4.3. Сделав подстановку (4.64), будем иметь уравнение

, (4.66)

где —новое выражение или график, учитывающий зависимость (4.64).

Таким образом, при однозначной нелинейности часто­та ω несимметричных автоколебаний остается такой же, как и при симметричных, независимо от величины сме­щения . Амплитуда же несимметричных колебаний α, определяемая уравнением (4.65), зависит от смещения и выражается через амплитуду симметричных автоко­лебаний α_с. Здесь не требуется решать уравнение (4.63).

Пример.4.14. В следящей системе (рис. 4.29) заданы в виде рис. 1.13 и передаточные функции:

Рис.4.29. Следящая система с идеальной релейной

характеристикой

Гармоническая линеаризация нелинейности (раздел 4.2) при симметричных колебаниях дает

а при несимметричных —

(4.67)

где, согласно (4.32),

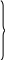
(4.68)

Уравнение замкнутой системы относительно переменной х (рис. 4.29) имеет вид

(4.69)

При симметричных автоколебаниях ( ) имеем характеристическое уравнение

Подставив , получим

Откуда

(4.70)

Рассмотрим несимметричные автоколебания при зада­ющем воздействии . В соответствии с (4.62), (4.68) и (4.69) получаем уравнение для постоянных со­ставляющих

откуда находим

(4.71)

Подстановка (4.71) в выражение для q (4.68) дает

Теперь для определения амплитуды α несимметрич­ных автоколебаний используем уравнение (4.66), а имен­но

Откуда

, (4.72)

где α_с определяется соотношением (4.71). Тогда, соглас­но (4.71), постоянная составляющая (смещение) опре­деляется в виде

(4.73)

Рис.4.30. Зависимости

α и от g₁

Частота же ω несимметричных автоколебаний будет прежней (формула 4.70).

Результаты (4.72) и (4.73) представлены графически на рис. 4.30.

Пример 4.15. Исследуем ту же систему (рис. 4.29), но с несимметричной нелинейностью вида рис. 4.31,а при задающем воздействии . Уравнение системы:

Причем вычисляется по формуле (4.67), где аналогично примеру 4.10 раздела 4.2 имеем

(4.74)

(4.75)

а) б)

Рис.4.31. Зависимости α и от g₁ для

несимметричной нелинейности

Уравнение для постоянных составляющих (4.62), с учетом того, что здесь , запишется в виде

откуда согласно(4.74) имеем

(4.76)

Характеристическое уравнение для периодических со­ставляющих в соответствии с (4.62) запишется в виде

П осле подстановки получаем

Откуда

Последнее уравнение с подстановкой (4.75) и (4.76) приобретает вид

Отсюда определяется величина смещения , после чего вычисляется амплитуда α по формуле (4.76). Результа­ты представлены на рис. 4.31, б.