Лекция 4 Термодинамический процесс

Взаимодействие системы с окружающей средой всегда сопровождается изменением некоторых термодинамических параметров (хотя бы координат состояния системы). Изменений значений параметров системы означает изменение состояния системы. Иначе говоря, система при взаимодействии с окружающей средой переходит из одного состояния в другое. Этот переход системы из одного (начального) состояния в другое (конечное) называют термодинамическим процессом. Термодинамический процесс можно так же определить как последовательное изменение состояния системы при её взаимодействии с окружающей средой, или как совокупность последовательных состояний системы, которые она принимает при ее взаимодействии с окружающей природой. Признаком протекания в системе термодинамического процесса является изменение её параметров состояния.

Все термодинамические процессы делятся на равновесные и неравновесные. Термодинамический процесс называется равновесным, если при его осуществлении все состояния, которые принимает система, являются равновесными.

Процесс называется неравновесным, если некоторые состояние, которые система принимает по ходу протекания процесса, являются неравновесными.

Математически термодинамический процесс выражается функциями, которые связывают некоторые параметры состояния системы. Такие уравнения называется уравнениями процесса. Для термомеханической равновесной системы уравнения процессов обобщённо можно представить в следующих видах

, , , , , .

Из этих шести уравнений надо выбрать три, которые попарно связываю разные параметры, например , , , или , , .

У термомеханической неравновесной системы такая тройка уравнений будет характеризовать изменения, протекающий только в одной точке системы. Для другой точки потребуется своя тройка уравнений. Поскольку таких точек бесконечное множество, то, в итоге, для математического описания неравновесного процесса потребуется бесконечное множество троек уравнений.

Обычно уравнение процесса получают из уравнения состояния фиксацией значения одного из параметров, либо совместным решением уравнения состояния и уравнения, выражающего дополнительное условие, характеризующее рассматриваемый процесс.

Графически уравнение равновесного процесса (для термомеханической системы) выражается пространственной линией, лежащей на поверхности, определяемой уравнением состояния системы (см. рис.4).

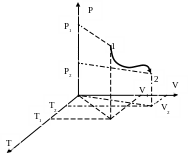
Рис. 4

На рисунке 4 точка 1 изображает состояние, характеризующее начало процесса, точка 2 – состояние конца процесса. Также обычно направление процесса обозначают стрелкой.

На координатных плоскостях или диаграммах равновесный термодинамический процесс также изображается линиями, которые являются проекциями пространственной линии (см. рис.5).

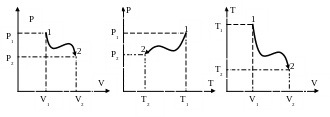
Рис. 5

Неравновесный термодинамический процесс графически изображается пространственной областью (см. рис.6).

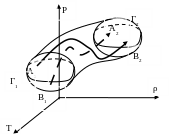
Рис. 6

На рис. 6 точка А₁ изображает начальное состояние в точке А системы, точка А₂ – конечное состояние в точке А, точка B₁ – начальное состояние в точке B, B₂ – конечное состояние в точке B. Сплошная линия А₁-А₂ изображает процесс, протекающий в точке А системы, штриховая линия B₁-B₂ - процесс, протекающий в точке B. Поверхность Г₁ изображает границу начального состояния 1 системы, Г₂ – конечного состояния 2.

Для выявления макроскопического критерия, устанавливающего различие между равновесным и неравновесным процессами, рассмотрим механизм протекания термодинамического процесса в системе под воздействием внешнего возмущения.

Будем считать, что в начальный момент времени неизолированная система находится в состоянии равновесия с окружающей средой. Спустя некоторое время параметры окружающей среды изменяются. Для определённости будем считать, что изменилось значение потенциала одного из типов взаимодействия. Это приводит к тому, что появляется разность значений этого потенциала между системой и окружающей средой на границе системы. Эта разность значений, в силу определения потенциала взаимодействия, является причиной обмена энергией между системой и окружающей средой. При этом возмущение, т.е. подвод или отвод энергии в рассматриваемой форме, не распространяется мгновенно по всей системе, а воспринимается только той частью системы, которая непосредственно соприкасается с границей системы. Подвод или отвод энергии приводит, в соответствии с выражениями (14) и (15), к изменению значения координаты состояния системы, соответствующей рассматриваемому типу взаимодействия. В свою очередь, изменение значения координаты состояния, в соответствии с уравнением состояния (20), вызывает в этом слое системы изменение значения потенциала взаимодействия, причём, согласно условиям устойчивости равновесия системы (21), это изменение компенсирует разность значений потенциала системы и окружающей среды. Это обстоятельство прекращает обмен энергией между системой и средой, но, с другой стороны, появляется разность значений потенциала взаимодействия между пограничным слоем системы и прилежащим к нему внутренним слоем. В результате происходит обмен энергией между этими слоями. Этот процесс протекает до тех пор, пока полученное из окружающей среды возмущение не передастся к самым удалённым от границы точкам системы, и во всей системе не выровняется значение потенциала. Термодинамический процесс будет являться равновесным тогда, когда следующую порцию возмущения система получит из окружающей среды только после того, как перейдёт в равновесное состояние. Если же новая порция возмущения будет получена системой до того, как старая порция достигнет каждой её точки, то в этом случае разность значений потенциала между слоями системы будет накапливаться, и система всё время будет находиться в неравновесном состоянии, т.е. процесс будет неравновесным.

Рассмотренный механизм взаимодействия системы с окружающей показывает, что, для того, чтобы процесс был равновесным независимо от величины разности потенциала системы и среды, изменение потенциала окружающей среды должно протекать сколь угодно долго. Иначе говоря, скорость протекания равновесного термодинамического процесса должна быть сколь угодно мала.

Все реальные процессы протекают с конечной скоростью при конечной разности параметров у системы и окружающей среды. Это значит, что все реальные процессы в той или иной степени не равновесны. Равновесный же процесс является идеализированной моделью, предельным случаем реального процесса.

Сравнивая математическое и графическое представление равновесного и неравновесного процессов, видно, что равновесный процесс значительно проще описывать, а значит и использовать в расчётах, чем неравновесный.

Для того, чтобы появилась возможность упрощённого описания и расчёта реальных термодинамических процессов, в рассмотрение вводят понятие «квазиравновесный процесс». Квазиравновесный процесс – это действительный процесс, время протекания которого больше времени релаксации системы. С учётом этого для описания квазиравновесного процесса можно использовать выражения, применимые к равновесному процессу. В дальнейшем все процессы будут рассматриваться как квазиравновесные.

Работа

В дальнейшем будем рассматривать только термомеханические системы и, в связи с этим, под работой будем понимать только механическую работу расширения.

Термин «работа» имеет два значения. В первом значении термин «работа» указывает на способ взаимодействия с окружающей средой, у которого координатой состояния является объём, занимаемый системой, а потенциалом взаимодействия – давление, взятое с отрицательным знаком. Иначе говоря, если система обменивается работой с окружающей средой, то это происходит под действием разности давлений, и при этом система изменяет свой объём. В силу этого механическую работу называют также работой расширения.

Под вторым значением термина «работа» понимается количество энергии, которым система обменивается с окружающей средой при взаимодействии, сопровождающимся изменением объёма. Поскольку работа – это энергия, то единица измерения работы – джоули, Дж. Исходя из второго смысла работы, величина работы, обозначаемая L, с учётом таблицы 1 и выражений (14) и (15) определяется выражениями

,	(23)
.	(24)

В этих выражениях знак «минус» перед давлением устранён для того, чтобы не использовать отрицательные числа. Выражение (24) показывает, что работа положительна, если объём системы возрастает, т.е. , и работа отрицательна, если система сжимается, т.е. . При этом говорят, что «система совершает работу», или что «работа отводится от системы», если работа положительна (см рис. 7).

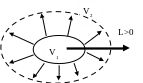
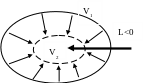
Рис. 7. Рис. 8.

Если же работа отрицательна (см. рис. 8), то в этом случае говорят, что «над системой совершается работа», или «работа затрачивается», или «работа подводится к системе».

Работу графически удобно изображать в P-V системе координат. Учитывая выражение для величины работы (24) и, известное из курса математического анализа, графическое представление определённого интеграла как площади под линией подынтегральной функции, можно утверждать, что величина работы в P-V диаграмме равна площади под линией процесса (см. рис.9).

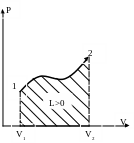
Рис. 9.

Работа является функцией процесса. Это значит, что величина работы зависит от типа процесса, посредством которого система переходит из одного состояния в другое.

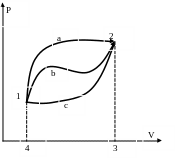
Рис. 10.

На рисунке 10 изображены три процесса 1-а-2, 1-b-2 и 1-с-2, которые переводят систему из состояния 1 в состояние 2. Сравнивая площади фигур 1-а-2-3-4, 1-b-2-3-4 и 1-с-2-3-4, а так же учитывая, что площадь под линией процесса в P-V диаграмме равна работе в этом процессе, можно сделать вывод, что работа в процессе 1-а-2 больше работы в процессе 1-b-2, которая, в свою очередь, больше работы в процессе 1-с-2 ( ).

Работа является аддитивной величиной. Это значит, что работа какой-либо совокупности процессов равна сумме работ этих процессов

.

(25)

Это свойство работы вытекает из определения работы как интеграла (24) и из геометрических свойств интеграла (см. рис.11).

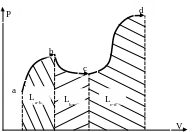
Рис. 11.

Работа расширения является экстенсивной величиной. Это следует из того, что объём зависит от массы вещества в системе, т.е.

.

(26)

Подставляя (26) в (24), для замкнутой системы с постоянной массой получим

.

(27)

Вводя в рассмотрение удельную работу

(28)

как работу, совершаемую одним килограммом вещества (Дж/кг), можно записать, что

.

(29)

Из этого свойства работы, т.е. из того, что работа пропорциональна массе системы, а так же из аддитивности массы следует, что работа системы равна сумме работ всех частей системы.