Основные термодинамические процессы в области газа

К основным термодинамическим процессам относиться: изохорный, изобарный, изотермический, адиабатный, политропный и процесс дросселирования.

Изохорный процесс

Изохорный процесc- это процесс, протекающий при постоянном объеме

V=ConsT; dV=0.

Для идеального газа уравнение изохорного процесса, связывающие между собой основные термодинамические параметры, вытекает из уравнения состояния идеального газа.

Если m и V – постоянные величины, то постоянно и отношение

.

Это же соотношение можно выразить через начальные и конечные параметры

.

(88)

Уравнение (88) и является уравнением изохорного процесса. Из него следует, что при увеличении температуры давление газа возрастает.

Работа в изохорном процессе равна нулю

,

т.к. объём газа не изменяется. Поэтому теплота, подведенная или отведенная, определяется, на основе 1-го закона термодинамики, как

, ,

(89)

где m – масса газа.

Изображение изохорных процессов в P-V диаграмме представлено на рис. 19

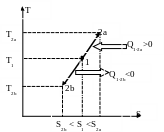
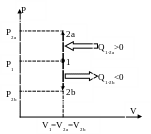
Рис. 19 Рис. 20.

Процесс 1-2a протекает с повышением давления, 1-2b – с понижением. Т.к. давление в процессе 1-2a повышается, то, в силу (88), возрастает и температура, что, в свою очередь говорит о том (см. (89)), что теплота положительна, т.е. подводится. В процессе 1-2b теплота отрицательна и отводится.

Чтобы получить изображение изохорного процесса и T-S диаграмме, надо получить зависимость температуры T от энтропии s для изохорного процесса. Для этого подставив выражение в (45), получим

.

Проинтегрировав это выражение в пределах от T₁ до T, получим

.

Из этого уравнения следует, что

.

(90)

Таким образом, изохора в T-S диаграмме является графиком экспоненты, которую, учитывая удалённость рассматриваемой области от начала координат, можно изображать наклонной прямой (см. рис. 20).

Изобарный процесс

Изобарный процесc - это процесс, протекающий при постоянном давлении

P=ConsT; dP=0.

Для идеального газа уравнение изобарного процесса, связывающие между собой основные термодинамические параметры, вытекает из уравнения состояния идеального газа.

Если m и Р – постоянные величины, то постоянно и отношение

.

Это же соотношение можно выразить через начальные и конечные параметры

.

(91)

Уравнение (88) и является уравнением изобарного процесса. Из него следует, что при увеличении температуры объём газа возрастает.

Работа в изохорном процессе определяется выражением

.

(92)

Предпоследнее равенство основано на уравнении состояния идеального газа.

Количество теплоты, которым система обменялось с окружающей средой, можно определить, с одной стороны, через теплоёмкость

,

(93)

а с другой стороны, через первый закон термодинамики

.

(94)

Сравнивая выражения (93) и (94), можно получить уравнение Майера, связывающее изобарную и изохорную теплоёмкости

,

(95)

которое справедливо только для идеального газа. Из этого уравнения следует, что изобарная теплоёмкость газа больше изохорной теплоёмкости.

Изображение изобарных процессов в P-V диаграмме представлено на рис. 21

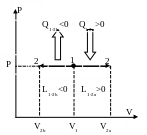
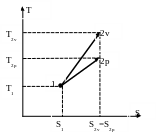
Рис. 21 Рис. 22.

Процесс 1-2a протекает с повышением объёма, 1-2b – с понижением. Поэтому работа в процессе 1-2a положительна, т.е. совершается системой, а в процессе 1-2b – отрицательна, т.е подводится к системе извне.

Т.к. объём в процессе 1-2a увеличивается, то на основе (91) температура возрастает, а это означает, в соответствии с (93), что теплота положительна и подводится к газу. Соответственно, в процессе 1-2b температура понижается, а теплота отводится, т.е. отрицательна.

Чтобы получить изображение изохорного процесса и T-S диаграмме, надо получить зависимость температуры T от энтропии s для изобарного процесса. Рассуждения в этом случае проводятся точно такие же, как и в случае изохорного процесса. В результате получается следующая зависимость температуры от энтропии

.

(96)

Отличие от изохорного процесса состоит в том, что в знаменателе показателя степени экспоненты находится изобарная теплоёмкость. Т.к. она меньше изохорной, то показатель экспоненты в изобарном процессе меньше показателя экспоненты для изохорного процесса. Это значит, что график изохорного процесса в T-S диаграмме идёт «круче» графика изобарного процесса (на рис. 22 изохорный процесс изображён линией 1-2v, а изобарный – линией 1-2р). Этот факт можно обобщить и утверждать, что изохорный процесс в любой области T-S диаграммы идёт «круче» изобарного.
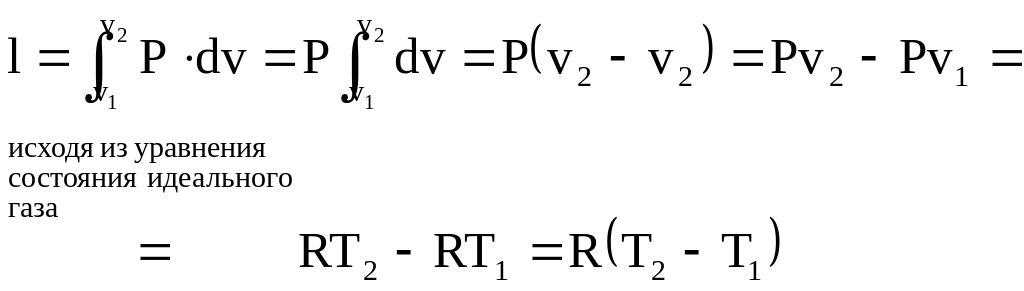