5.3. Дисперсія, різні оцінки швидкостей

Властивості середовищ, в яких поширюються реальні електромагнітні процеси, завжди є в тій чи іншій мірі частотно залежними, тобто і . Тому повинна залежати від частоти і фазова швидкість ЕМ хвиль. Така залежність параметрів поширення хвилі від частоти називається дисперсією.

Г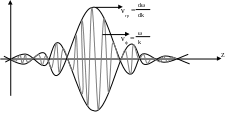 рупова швидкість. Реальні сигнали містять багато гармо-нічних складових з різними частотами. Сигнал має спектр, тому напруженості ЕМ поля можуть бути представлені інтегралом Фур’є:

,

де – групова швидкість.

Групова швидкість – це швидкість поширення огинаючої сигналу, якщо залежність фазової швидкості від частоти є достатньо малою (див. рис).

В протилежному випадку частотні складові мають різні швидкості, що приводить до спотворення форми огинаючої. Тоді простежити за переміщенням якої-небудь точки на цій огинаючій неможливо, тобто „швидкість поширення сигналу” втрачає сенс.

Можна показати, що при відсутності втрат групова швидкість співпадає зі швидкістю переносу енергії. Це твердження є справедливим і в тому випадку, коли втрати малі і слабо залежать від частоти. Але, якщо втрати великі, то швидкість може відрізняється від , причому остання може інколи перевищувати швидкість світла. При цьому поняття групової швидкості втрачає фізичний зміст.

Групову швидкість плоскої однорідної хвилі можна знайти за такою формулою:

.

Таке співвідношення називають формулою Релея. Із цього співвідношення слідує, що фазова і групова швидкості можуть бути різними не тільки за значенням, але і за знаком. Зв’язок між фазовою і груповою швидкостями може бути ще представлений такою формулою: , де – хвильове число. Тому можна зробити висновок, що може бути як більше, так і менше фазової, але завжди  c.

Розрізняють наступні види дисперсій:

– позитивна дисперсія – коли напрямки поширення і співпадають;

– негативна дисперсія – коли напрямки поширення і протилежні;

а за знаком похідної фазової швидкості:

– нормальна дисперсія – якщо .

– аномальна дисперсія – якщо .

Виходячи з рівності (5.17) можна зробити висновок, що негативна аномальна дисперсія неможлива, оскільки: .

5.4. Поляризація електромагнітних хвиль

Вище знайдені рівняння (2) і (4) із (5.9): та (5.18)

мають аналогічні розв’язки, що і рівняння (1) і (5) із (5.9), тому аналогічно, як (5.11) і (5.12) отримаємо: та . (5.19)

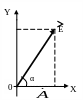
В загальному випадку е/м поле для падаючої ( ) хвилі містить дві поперечні складові (див. рис.):

. (5.20)

Порахувавши скалярний і векторний добуток цих величин не важко переконатись, що при довільних і вектори і утворюють з напрямком поширення z_o праву трійку ортогональних векторів. Тобто, якщо позначити , тоді можна записати:

і . (5.21)

Тобто вектори і є повністю рівнозначні і розглядати можна якийсь один. Напрям кожного з цих векторів може змінюватись в просторі в залежності від співвідношення комплексних амплітуд і . Для миттєвого значення поля значення напруженості поля:

= cos( , (5.22)

де A_m та C_m – амплітуди проекцій вектора на осі X та Y відповідно.

Тоді модуль вектора : E(z,t)= , (5.23)

а фаза вектора : . (5.24)

З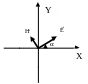 алежність кута від z і t визначає поляризацію хвилі (див. рис). Розглянемо деякі види поляризацій.

1) Лінійно поляризованою називають хвилю, у якої напрямок коливань векторів відбувається в одній площині та у довільній точці простору залишається незмінним зі зміною часу. Якщо початкові фази хвиль співпадають ( ) або зсунуті одна відносно другої на , то суперпозиція хвиль дає результуючу хвилю, яка також буде мати лінійну поляризацію.

Тобто, якщо , тоді

E(z,t)= та (5.25)

Площина, що проходить через напрямок поширення електромагнітної хвилі і вектор , називається площиною поляризації.

2) Поляризованою по колу називають хвилю, у якої вектори в довільній точці простору рівномірно обертаються, описуючи за час одного періоду Т своїми кінцями кола.

П рипустивши і , отримаємо:

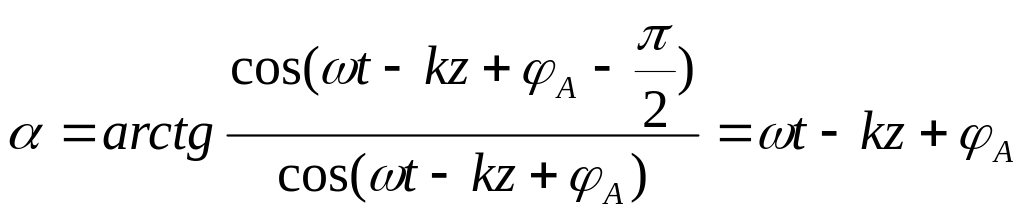E(z,t)= та . (5.26)

тобто довжина вектора залишається сталою, а кут лінійно залежить від координати і часу, обертаючись з кутовою швидкістю . При t=const кінець вектора описує спіраль з кроком .

Два види колової поляризації:

– ліва колова поляризація при ; та права колова поляризація при .

У випадку правої кругової поляризації вектор повертається за годинниковою стрілкою (якщо дивитися вздовж напряму поширення хвилі), а у випадку лівої кругової поляризації – проти годинникової стрілки.

Будь-яку хвилю з лінійною поляризацією можна розкласти на дві хвилі з правою і лівою коловою поляризацією (див. рисунок).

Площина поляризації хвилі, яка обертається по колу, в кожній точці простору рівномірно обертається із зміною часу.

3). Еліптично поляризованою хвилею називають хвилю, в якої вектори і в довільній точці простору обертаються , описуючи за час одного періоду Т своїми кінцями еліпси.

В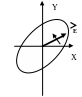 ідмітимо, що в тих випадках, коли аналізована плоска хвиля не являється однорідною (коли поверхні рівних амплітуд не співпадають з поверхнями рівних фаз), поляризація хвилі може бути різноманітною в різних точках площини, перпендикулярних до напрямку поширення хвилі (осі Z)

У випадку немонохроматичних процесів, крім поляризованих хвиль, можуть існувати також неполяризовані або частково поляризовані хвилі. Неполяризованими називають хвилю, у якої вектори і хаотично, випадковим чином змінюють свій напрямок в площині, що перпендикулярна напрямку поширення. Частково поляризованою називають хвилю, що складається з поляризованої та неполяризованої складових хвиль.