44

5. Електромагнітні хвилі та коливання.

5.1. Гармонічні хвилі

У більшості випадків електромагнітне поле змінюється в часі за гармонічним законом (тобто за законом косинуса або синуса, різниця між якими лише у різниці фаз на ).

Основні визначення розділу:

1). Період (Т) – це проміжок часу, протягом якого точка хвилі проходить шлях між однойменними точками. Розмірність [c], (секунда).

2). Довжина хвилі ( ) – це відстань, яку проходить сигнал за час одного періоду. Розмірність [м], (метр).

3). Частота ( f ) – це величина, яка показує кількість змін поля протягом часу, який рівний одному періоду. Розмірність [Гц], (герц). [Гц]=1/[с].

Н ехай маємо скалярну функцію u від однієї координати z і часу t. Тоді для плоскої однорідної хвилі в недеформуючому середовищі можна записати:

,

де v – швидкість поширення хвилі.

Для гармонічної хвилі:

, де k=/v=2f/v – хвильове число;v– фазова швидкість.

Просторовий період називають довжиною хвилі , тобто . Отже:

U(z,t)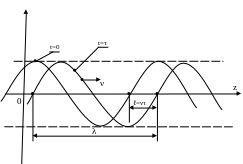

, [1/м] (5.1)

Тоді . (5.2)

Поширення гармонічної хвилі відображається зміщенням косинусоїди вздовж осі z зі швидкістю v.

(1) Розглянемо випадок формування стоячої хвилі. Нехай назустріч один одному поширюються дві хвилі, для яких справедливо:

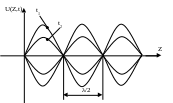
Якщо і , тоді:

– це стояча хвиля, в якій амплітуда залежить від z. В кожний момент часу ми маємо нерухому косинусоїду, нулі якої не зміщуються вздовж осі Z, а залишаються фіксованими. Тут ці нулі називаються вузлами, а середні значення між ними – пучностями стоячої хвилі.

(2) Використаємо метод комплексних амплітуд, для якого:

(5.3)

Введемо позначення:

,

тобто: – це при . Тоді .

В рамках методу комплексних амплітуд, хвильові числа можуть бути комплексними, тобто:

, тоді . (5.4)

П ри – затухаюча хвиля, тому – коефіцієнт затухання, – коефіцієнт фази. Коефіцієнт затухання – показує, як зменшилася амплітуда електромагнітної хвилі на кінці відрізку у порівнянні з його початком. Коефіцієнт фази – показує зміну фази при поширенні електромагнітної хвилі вздовж напряму Z. Тоді відношення амплітуд показує, в скільки разів зменшилась амплітуда затухаючої хвилі на шляху l. Але оскільки потужність прямо пропорційна квадрату амплітуди, тому частіше розглядають таке відношення: . Ці відношення логарифмують і отримують величину L, яку називають затуханням і яка вимірюється в неперах [Нп] або децибелах [дБ].

Для зменшення плутанини при розрахунках наведемо визначення кожної із цих величин:

1). Затухання в один непер [Нп] відповідає зменшенню потужності в е разів, а струму і напруги в разів:

. (5.5)

2). Затухання в один бел [Б] відповідає зменшенню потужності в 10 разів, а струму і напруги в 3.17 разів.

. (5.5а)

3). Затухання в один децибел [дБ] характеризує зміну потужності в 1.26 раз, а струму і напруги в 1.12 разів:

. (5.6)

тоді

. [дБ] (5.7)

Якщо хвильовий характер мають компоненти деякого вектора, то це – векторна хвиля. В загальному випадку:

. (5.8)

Тоді поверхня постійної фази – це є поверхня фронту, яка в загальному випадку може мати будь-яку форму, тобто бути неплоскою. Якщо на поверхні фронту амплітуда: , то хвиля є неоднорідною. Неплоска і неоднорідна хвиля може бути локально плоскою і локально однорідною. Це значить, що частина фронту, що розглядається досить близька до елементу площини.