1.2.1. Додавання векторів

Додавання векторів зводиться до сумування їх компонентів:

; (1.5)

Для двохмірного варіанта (тобто, значення координати z рівне нулю) сума векторів знаходиться за правилом трикутника чи правилом паралелограма.

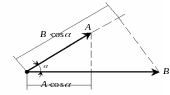
1.2.2. Скалярний добуток векторів

Скалярний добуток векторів і визначається таким чином:

(1.6)

де – косинус кута між векторами і . Звідси відома формула:

.

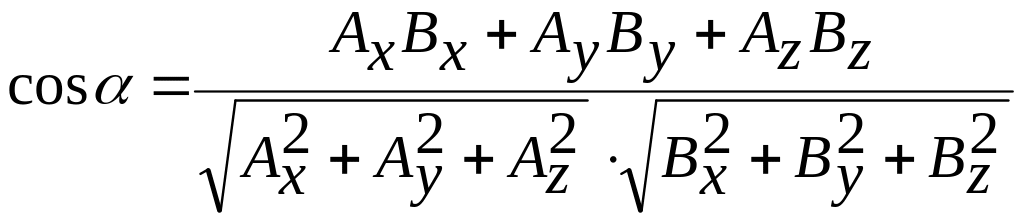Властивості:

1. Я кщо вектори , то ;

2. ;

3. ;

4. ;

5. .

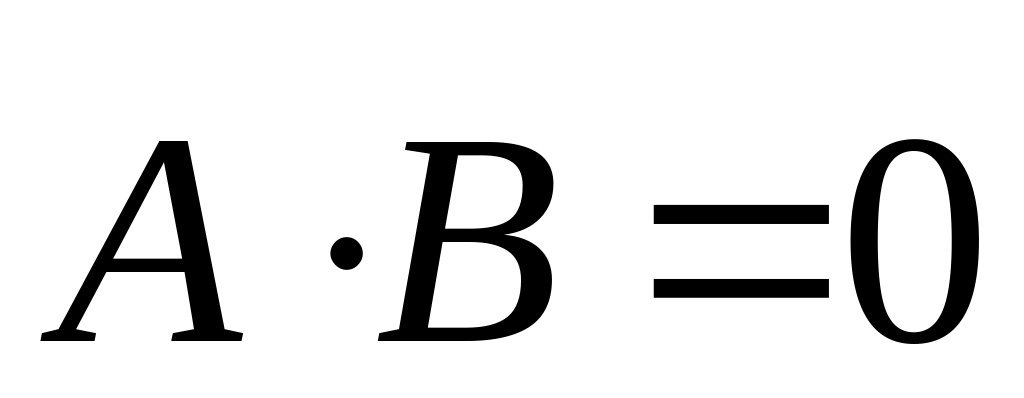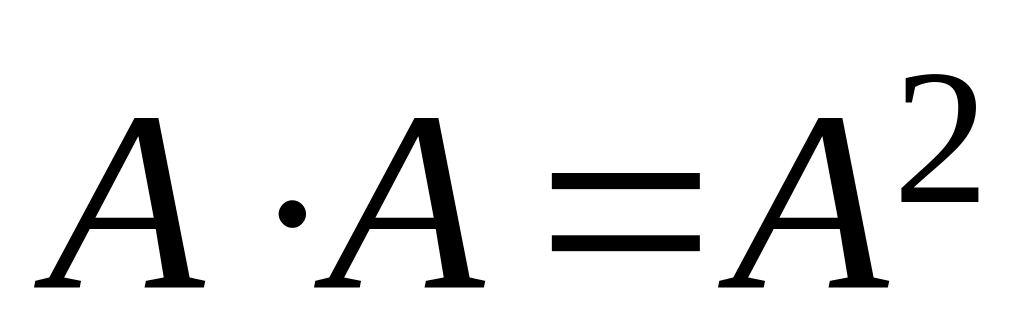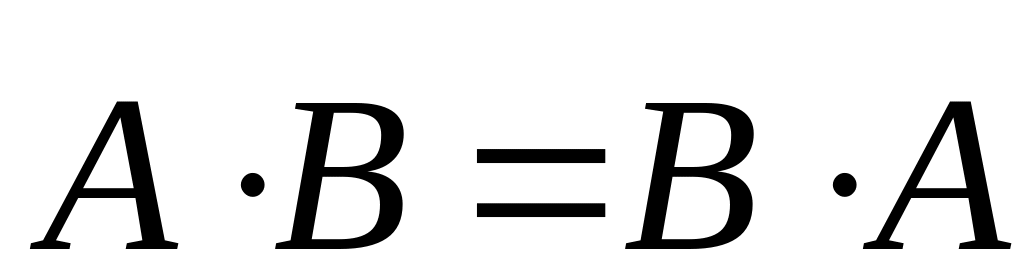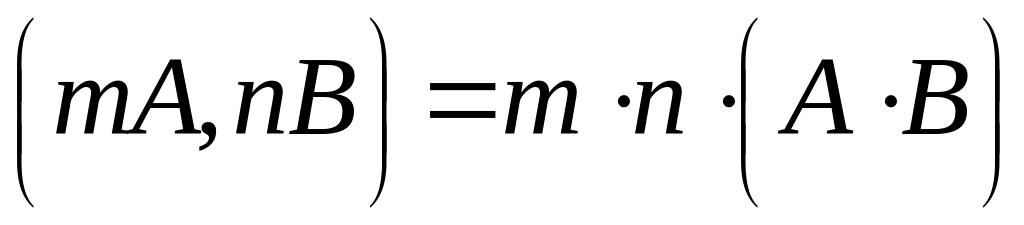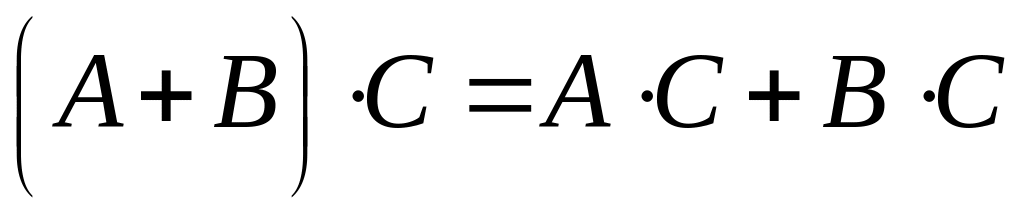6. Якщо , тобто 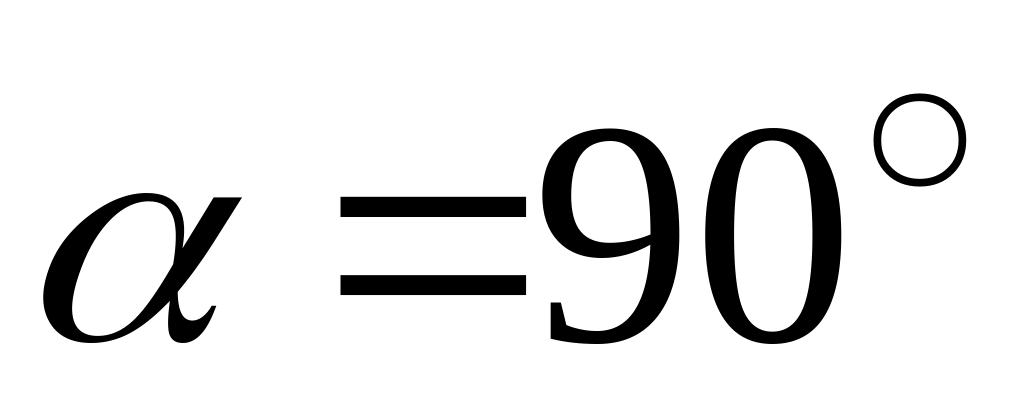, то вектори і наз. ортогональними.

1.2.3. Векторний добуток двох векторів

Векторний добуток і це є: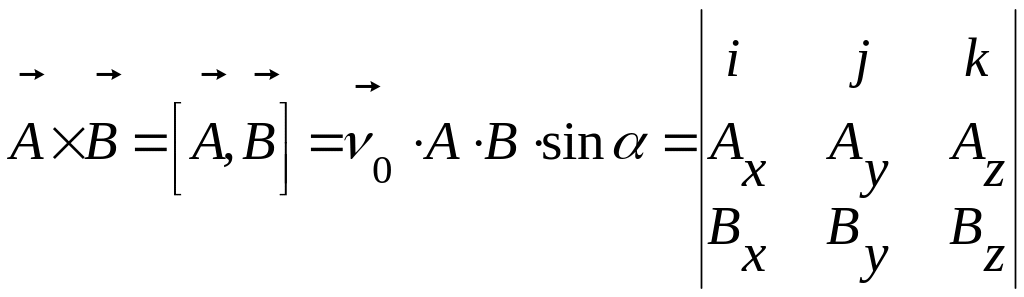 . (1.7)

д е – орт, направлений по нормалі до площини векторів і , причому так, що найменша кутова відстань між їхніми напрямками, позначена , відповідає переміщенню від до за годинниковою стрілкою, якщо дивитися вздовж .

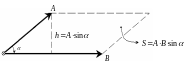
Геометричний зміст векторного добутку векторів і – це є площа паралелограма, побудованого на цих векторах

Властивості векторного добутку векторів:

1. Якщо , тобто  , то . Векторний добуток рівний нулю, коли вектори і паралельні.

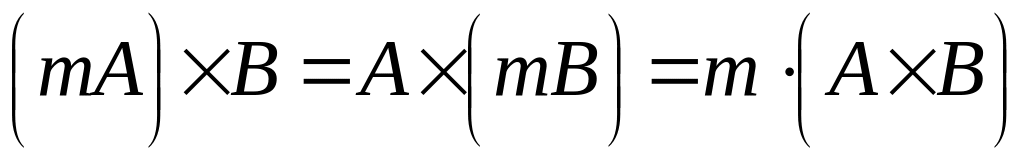2. , де 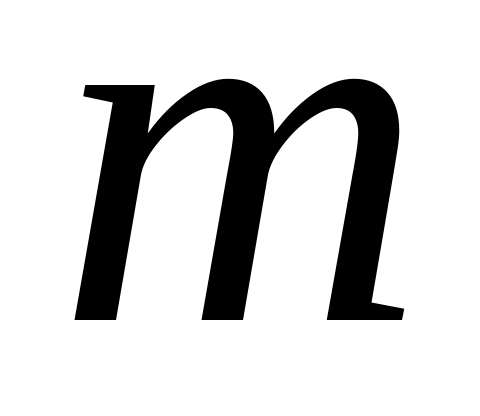– скаляр.

3. .

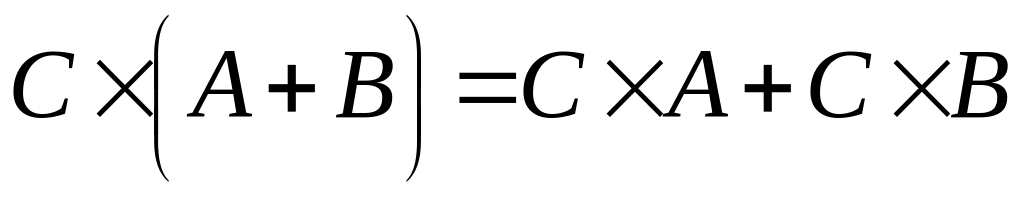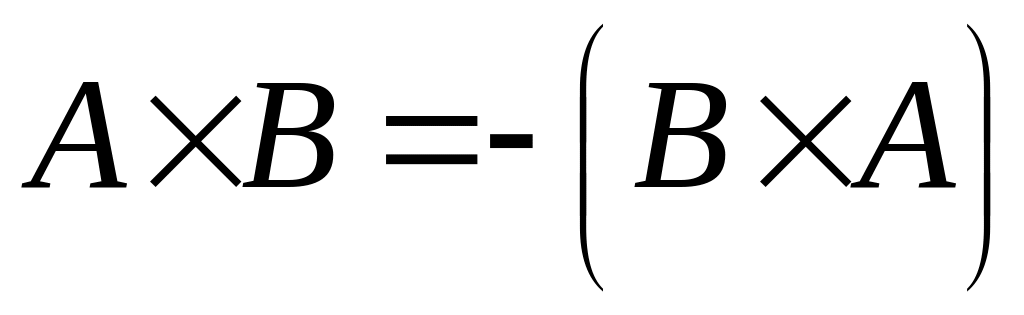4. . Від перестановки множників векторний добуток змінює знак.

Скалярні добутки декартових орт:

– для  орт; – для  орт.

Векторні добутки декартових орт:

	для  орт
}	для  орт

1.2.4. Змішаний (векторно-скалярний) добуток векторів

Для трьох векторів визначено добуток:

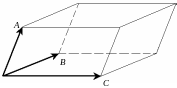
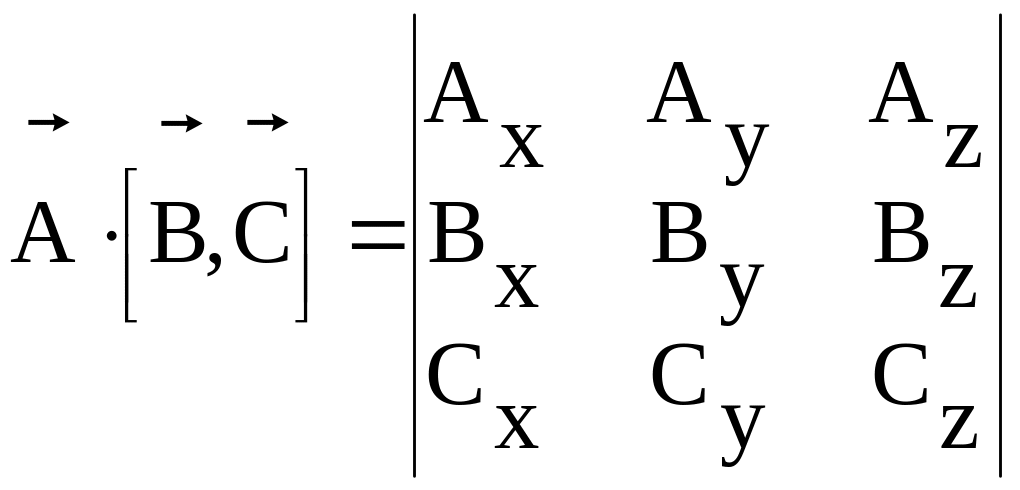. (1.8)

Геометрично – це є об’єм паралелепіпеда.

Властивості:

1. При циклічній перестановці векторів множників, змішаний добуток не змінюється: ;

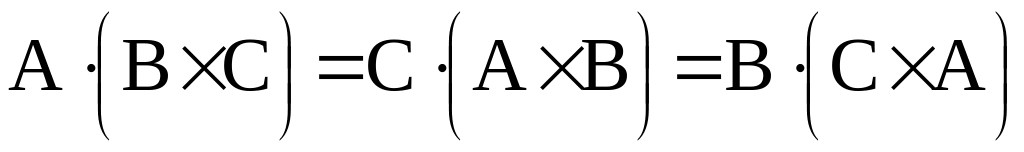2. При перестановці двох співмножників змішаний добуток змінює знак: ;

3. Змішаний добуток дорівнює нулю, якщо – компланарні.

1.2.5. Подвійний векторний добуток

Він розкривається за формулою:

. (1.9)

Тут скалярні добутки, що позначені за допомогою круглих дужок, входять як числа.

1.3. Градієнт

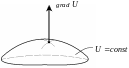
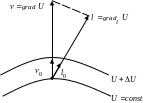
Нехай задано скалярне поле . Введемо вектор , що називається градієнтом U, який направлений у сторону максимального збільшення U і рівний швидкості зміни U у цьому напрямку (див. рис. зліва).

Очевидно, що: 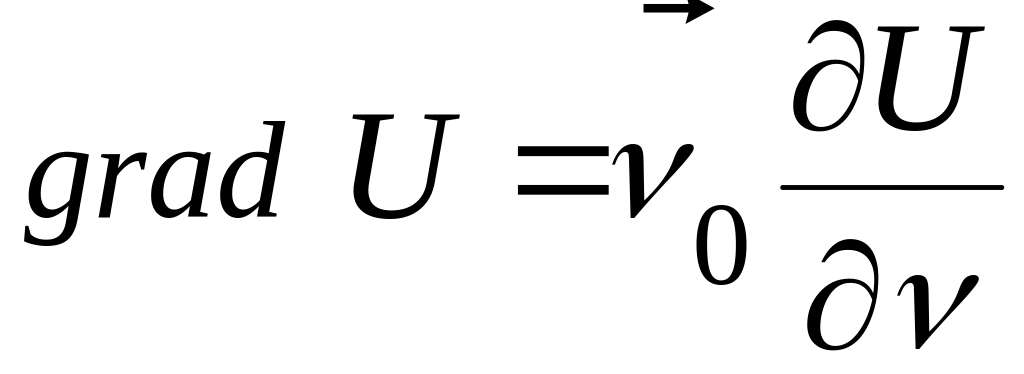, (1.10)

де – лінія, ортогональна до поверхні рівня. І: 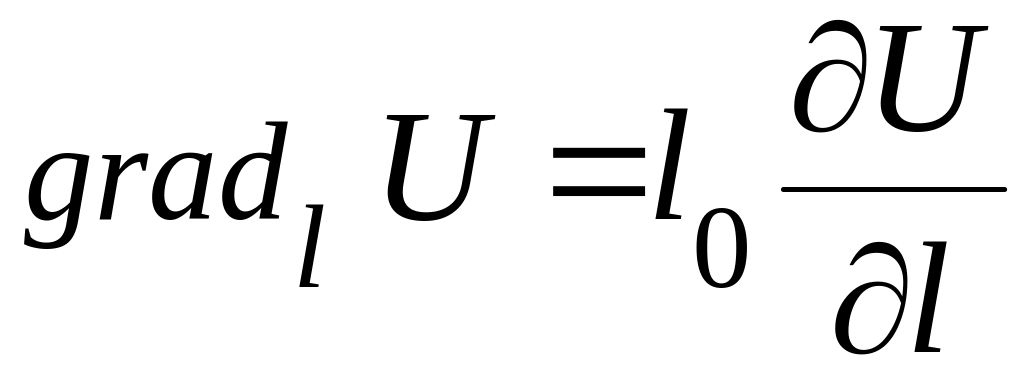. (1.11)

Тоді визначаючи проекції градієнта U в декартовій системі координат:

, , , маємо: 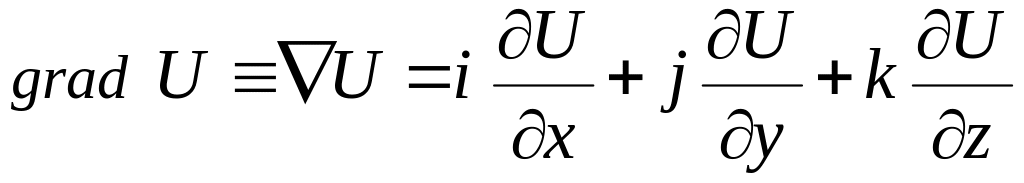. (1.12)

Скалярне поле U породжує векторне поле . Таке векторне поле називається потенціальним, а скалярна функція – потенціалом. Поверхні рівня, на яких , є еквіпотенціальними поверхнями. Тоді модуль градієнта рівний:

.

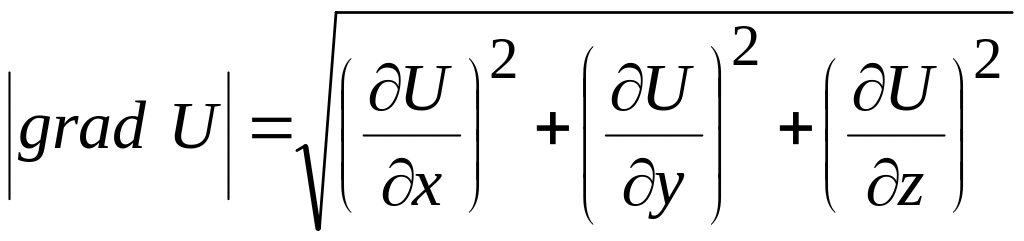
Стрілка градієнта вказує на напрямок найбільшої крутизни (рис. зліва) Градієнт ще називають просторовою похідною (рис. зверху справа).

1.4. Силові лінії

Для наглядного відображення векторний полів переважно будують картини так званих векторних, або силових ліній. Це лінії, дотичні до яких у кожній точці вказують напрямок вектора. Густина силових ліній може відповідати інтенсивності поля. При цьому кількість силових ліній, що проходять через ортогональну площадку, повинна бути пропорційна абсолютному значенню вектора, практично постійному в межах малої площадки (див. рис., де ).