2.3. Описание лабораторной установки

Лабораторная установка, подключаемая к регулируемому источнику постоянного напряжения в диапазоне от 0 до 60 В частотой 50 Гц, состоит из набора независимых регулируемых наборов активных сопротивлений, из которых набираются два канала, соединяемых обратным проводом. Номинальные значения постоянных и переменных сопротивлений приведены на рис.2.4.

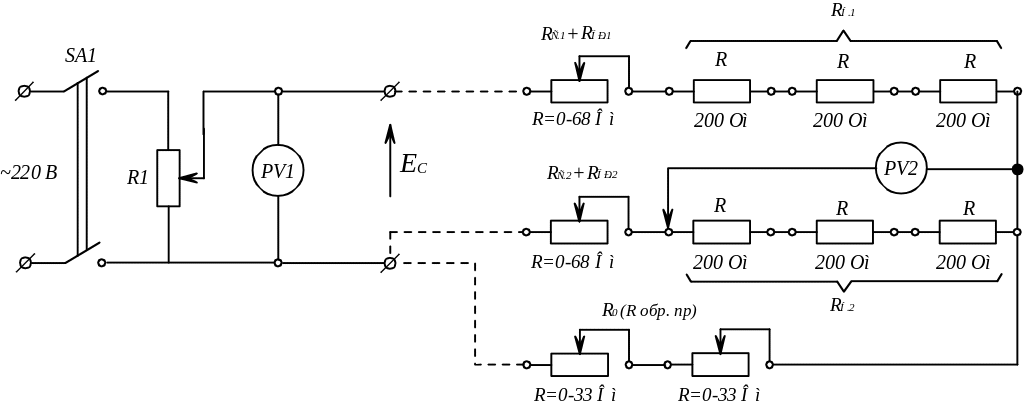
Рис.2.4.

Контроль Е_С осуществляется вольтметром РV1, а напряжение помехи (наводки) – вольтметром РV2.

2.4. Порядок проведения работы

1. Собрать схему с одним источником сигнала и произвольным набором сопротивлений R_С + R_ПР, R_Н, R₀. выставить заданное значение ЭДС сигнала (30 – 60 В) и замерить вольтметром РV2 напряжение помехи. Произвести несколько замеров напряжений помехи при различных сочетаниях Е_С и сопротивлений R_С1 + R_ПР1, R_С2 + R_ПР2, R_Н1, R_Н2, R₀. результаты свести в таблицу 2.1 и сравнить с результатами расчетов по выражению 2.1.

2. Аналогично произвести замеры напряжения помехи для частного случая (R_ПР1 = R_ПР2 = R₀; R_Н1 = R_Н2 = R_Н) при постоянном значении Е_С и различных соотношениях k = R_Н/ R₀. Результаты свести в табл.2.2 аналогичную табл.2.1. Построить график функции U_2* = f(k) для результатов эксперимента, сравнить данные эксперимента с расчетными по выражениям (1.2) и (1.3).

3. Убедиться, что при R₀→0 (устранение обратного провода) напряжение помехи также стремится к 0.

4. Сделать выводы по проделанной работе и оформить отчет.

Таблица 2.1

№ опыта	ЕС, В	R1= RС1 + RПР1, Ом	R1= RС2 + RПР2, Ом	RЭ1, Ом	RЭ2, Ом	R0, Ом	U2, В	U2*= =U2/ЕС	U2*расч
1
2
3

2.5. Содержание отчета по лабораторной работе

Отчет по лабораторной работе должен содержать:

а) схему экспериментов;

б) результаты экспериментов;

в) графические зависимости результатов экспериментов;

г) краткое объяснение полученных результатов и основные выводы по результатам.

2.6. Контрольные вопросы

1. На примере рисунка 2.3 объяснить зависимость величин сопротивления обратного провода и напряжения помехи.

2. Пояснить на примере рисунка 2.3 природу возникновения помехи.

3. Что такое гальваническая развязка? Привести примеры.

Лабораторная работа №3

Исследование влияния емкостных связей

3.1. Цель работы

Изучить влияние емкостных связей на уровни помех в гальванически развязанных электрических цепях.

3.2 Пояснения к работе

Рассмотрим два гальванически развязанных электрических контура, в котором, в общем случае, существуют емкостные связи между отдельными проводами контуров (рис.3.1). Рассмотрим наиболее простой случай, когда ЭДС Е_С1 действует только в одном контуре, тогда при наличии емкостных связей между проводами контуров С₁₃, С₁₄, С₂₃ С₂₄ во втором контуре возможно появление напряжения помехи U_ПОМ на нагрузке Z_Н2.

Примем в качестве допущения, что, в общем случае, распределенная емкость между проводом “m” и проводом “n” заменяется сосредоточенной емкостью С_mn. Под Z₁ и Z₂ будем подразумевать эквивалентные сопротивления источников ЭДС и сопротивлений проводов связи каналов, т.е. Z₁ = Z_С1 + Z_ПР1 и Z₂ = Z_С2 + Z_ПР2.

Можно показать, что схему по рис.3.1 можно представить в виде, показанном на рисунке 3.2,а., и с учетом активного характера сопротивлений (источников) канала связи и нагрузки в виде, показанном на рисунке 3.2,б.

Рис.3.1.

На схеме по рис.3.2.б приняты следующие обозначения:

Z₁=1/(jωC₁₄); Z₂=1/(jωC₂₄); Z₃=1/(jωC₁₃); Z₄ =1/(jωC₂₃); где ω = 2πf - угловая частота (ω=314 рад/с для f =50 Гц).

а)

б)

Рис.3.2

Таким образом, напряжение помехи U_ПОМ = U₃₄ выделяется на результирующем сопротивлении R_P, включенном в диагональ моста, образованного емкостями межпроводных связей.

Выражение для определения U₃₄ в общем виде слишком громоздко и трудно анализируется. Однако, учитывая, что емкости межпроводных связей достаточно малы, а соответственно сопротивления Z_С ≈ x_С значительно превышают активные сопротивления проводов и нагрузки, то можно принять напряжение диагонали

(3.1)

Используя метод эквивалентного генератора, можно легко определить напряжение помехи (наводки за счет электростатической индукции)

UПОМ = U34 = ,

(3.2)

где Е_Э = 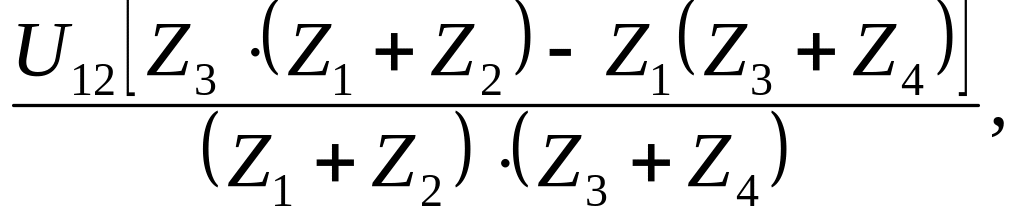(3.3) – ЭДС эквивалентного генератора;

ZЭ = ,

(3.4)

• сопротивление эквивалентного генератора.

Анализируя выражение (3.3) для Е_Э можно показать, что Е_Э = 0 и, соответственно, напряжение помехи U₃₄ = 0, если точки 3 и 4 эквипотенциальны. Это условие будет обеспечено при следующем соотношении емкостных сопротивлений

или ,

(3.5)

где k – любое число.

Наиболее простой случай - это равенство всех емкостей моста С₁₃ = С₁₄ = С₂₃ = С₂₄, т.е. Z₁ = Z₂ = Z₃ = Z₄. Естественно, чем больше отличаются соотношения Z₃/Z₁ и Z₄/Z₂, тем больше будет напряжение помехи. Поскольку с изменением частоты ω сопротивления Z₁, Z₂, Z₃, Z₄ будут изменяться одинаково, то соотношение Z₃/Z₁ и Z₄/Z₂ при изменении частоты останутся неизменными в широком диапазоне изменения ω = 2πf, практически неизменной остается ЭДС эквивалентного генератора Е_Э ≡ U₁₂, однако обратно пропорционально ω уменьшается сопротивление эквивалентного генератора , где Z_Э – сопротивление эквивалентного генератора при ω = 314 1/с; m = ω_m/314 – кратность увеличения частоты сигнала ω_m по отношению к ω при f = 50 Гц.

В результате напряжения помехи будет практически линейно возрастать с ростом угловой частоты ω. Однако при дальнейшем росте частоты сопротивление емкостного моста Z_М = (Z₁+ Z₂)║( Z₃+ Z₄) будет уменьшаться все сильнее и будет происходить шунтирование R_Н1, соответственно уменьшение напряжения диагонали U₁₂ и, тем самым, уменьшение помехи.