
Лекции_2
.docЛекция № 1. Множества и операции над множествами.
Определение 1.
Совокупность
объектов произвольной природы называется
множеством. Объекты, входящие в множество,
называются его элементами. Если x
элемент множества А,
то обозначают
![]() ,
если x
не является его элементом, то обозначают
,
если x
не является его элементом, то обозначают
![]() .
Если множество не содержит ни одного
элемента, то оно называется пустым
множеством ø.
.
Если множество не содержит ни одного
элемента, то оно называется пустым
множеством ø.![]()
Определение 2.
Пусть А и В множества.
Множество А является подмножеством В,
если каждый элемент А принадлежит В.
Обозначаем:
![]() ,
т. е.
,
т. е.
![]() .
.
Определение 3.
Говорят, что
множества А и В равны, когда они состоят
из одних и тех же элементов. Обозначаем:
![]() ,
т. е.
,
т. е.
![]() .
.
О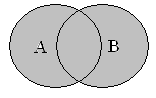 перации
над множествами:
перации
над множествами:
-
Объединение множеств.
Множество
![]() называется объединением множеств, если
состоит из элементов, каждый из которых
принадлежит хотя бы одному из множеств
А или В:
называется объединением множеств, если
состоит из элементов, каждый из которых
принадлежит хотя бы одному из множеств
А или В:
![]() .
.
-
П
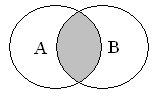 ересечение
множеств.
ересечение
множеств.
Множество
![]() называется пересечением множеств, если
состоит из элементов, каждый из которых
принадлежит и множеству А и В:
называется пересечением множеств, если
состоит из элементов, каждый из которых
принадлежит и множеству А и В:
![]() .
.
-
Р
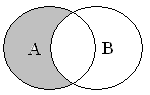 азность
множеств.
азность
множеств.
Множество
![]() называется разностью множеств (из А
вычитаем В), если состоит из элементов,
каждый из которых принадлежит множеству
А, но не принадлежит В:
называется разностью множеств (из А
вычитаем В), если состоит из элементов,
каждый из которых принадлежит множеству
А, но не принадлежит В:
![]() .
Заметим, что
.
Заметим, что
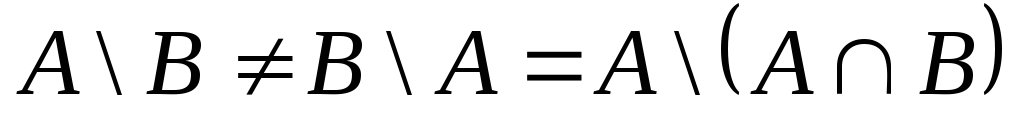 .
.![]()
3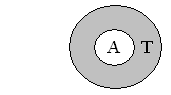 ’.
Дополнение одного множества до другого.
’.
Дополнение одного множества до другого.
Пусть
![]() .
Дополнением множества А до множества
T
называется множество
.
Дополнением множества А до множества
T
называется множество
![]() .
.
Некоторые числовые множества.
![]() – множество
натуральных чисел;
– множество
натуральных чисел;
![]() – множество целых
чисел;
– множество целых
чисел;
![]() – множество
рациональных чисел;
– множество
рациональных чисел;
![]() – множество всех
действительных чисел.
– множество всех
действительных чисел.
Заметим, что
![]() .
.
Определение 4.
Пусть
![]() .
.
![]() – отрезок;
– отрезок;
![]() – интервал;
– интервал;
![]() – полуинтервал;
– полуинтервал;
![]() – полуинтервал.
– полуинтервал.
Множества
![]() называются промежутками.
называются промежутками.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Множества
![]() называются бесконечными промежутками.
называются бесконечными промежутками.
Некоторые свойства вещественных чисел.
-
Свойство упорядоченности.
![]() .
.
-
Свойство непрерывности вещественных чисел.
Пусть А и В
произвольные непустые подмножества
множества R
такие, что
![]() ,
тогда
,
тогда
![]() .
.
Модуль действительного числа.
Пусть
![]() .
Тогда
.
Тогда
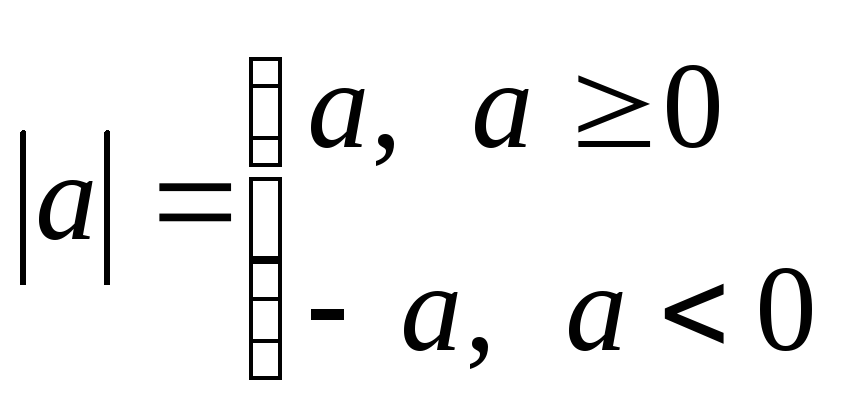
Свойства (![]() ):
):
-
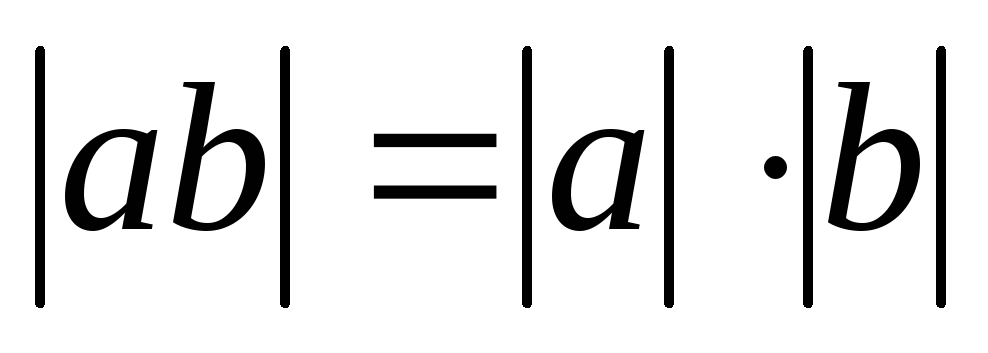
-
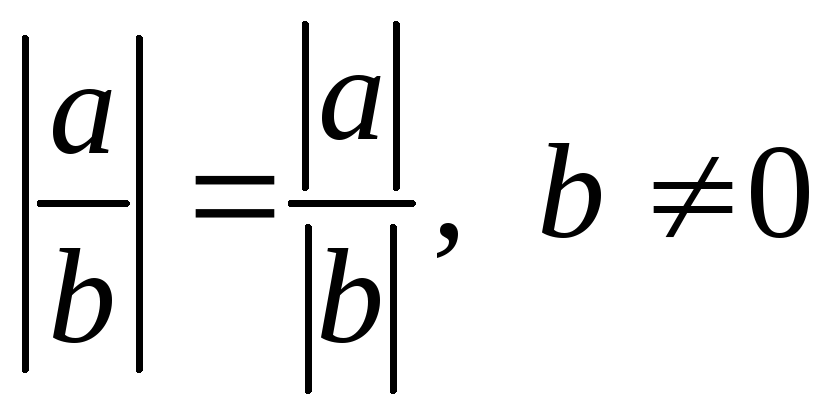
-
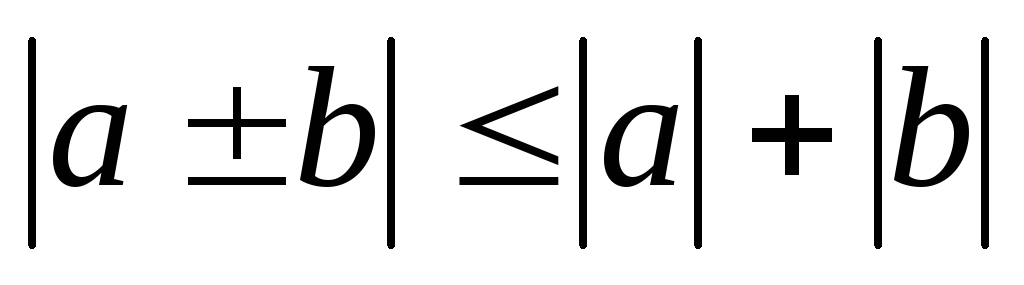
-
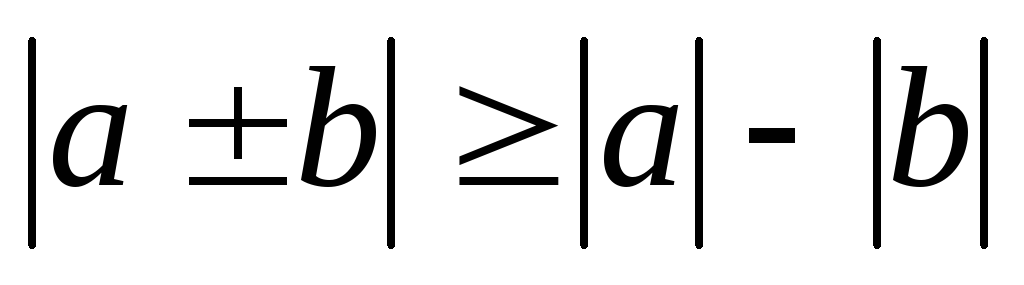
-
Пусть
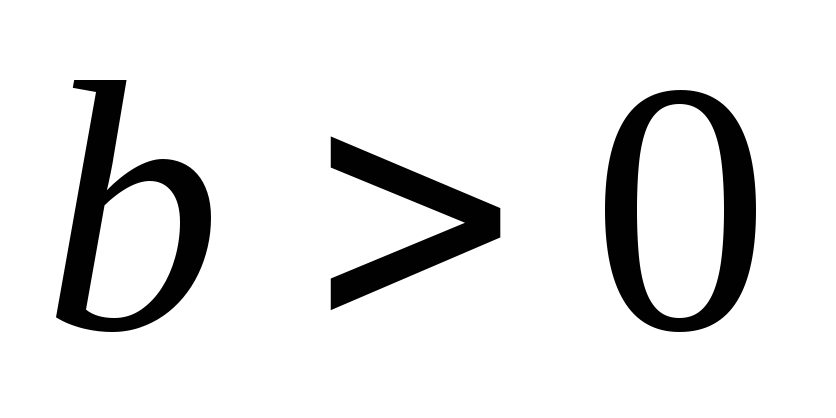 ,
тогда
,
тогда
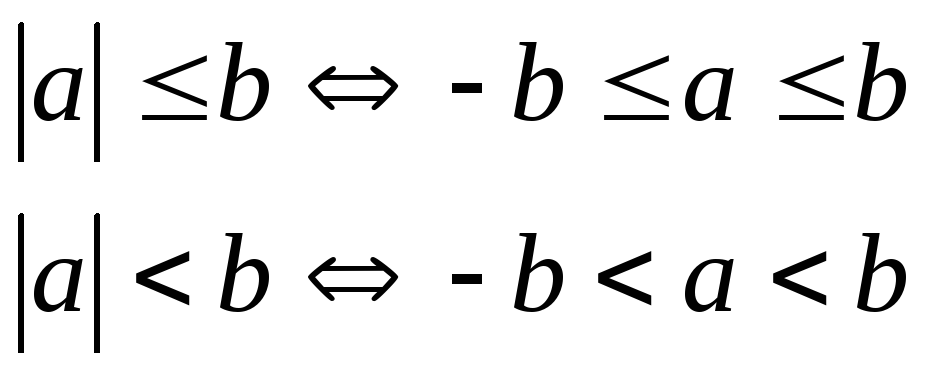
Лекция № 2. Ограниченные и неограниченные множества.
Определение 1.
М
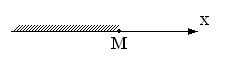 ножество
А называется ограниченным сверху
(снизу), если
ножество
А называется ограниченным сверху
(снизу), если
![]() (
(![]() ).
Число М – верхняя грань, m
– нижняя грань множества А.
).
Число М – верхняя грань, m
– нижняя грань множества А.
Определение 2.
М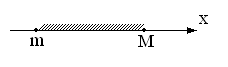 ножество
А называется ограниченным, если оно
ограничено сверху и снизу, т. е.
ножество
А называется ограниченным, если оно
ограничено сверху и снизу, т. е.
![]() .
.
Определение 2’ (эквивалентное).
Множество А
называется ограниченным, если
![]() .
.
Доказательство.
Докажем, что
определение 2 и 2’ эквивалентны, т.е.
![]()
![]()
![]()
![]() .
.
-
 Пусть
Пусть
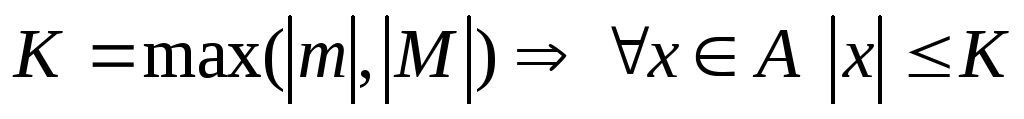 ,
т. е.
,
т. е.
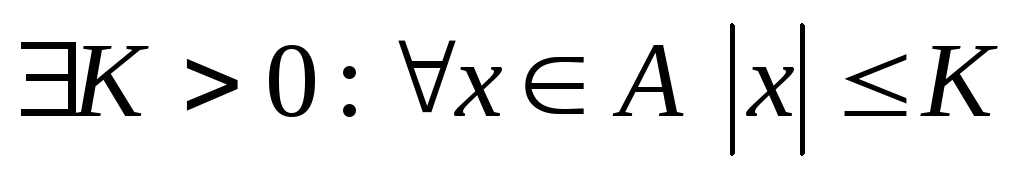
-

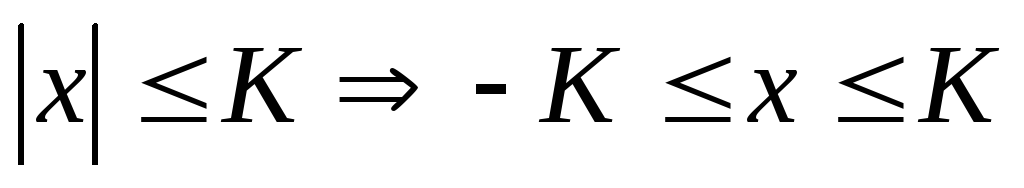
![]()
![]()
ч. т. д.
Определение 3.
Множество А
называется неограниченным, если
![]() .
.
Доказательство.
-
Фиксируем
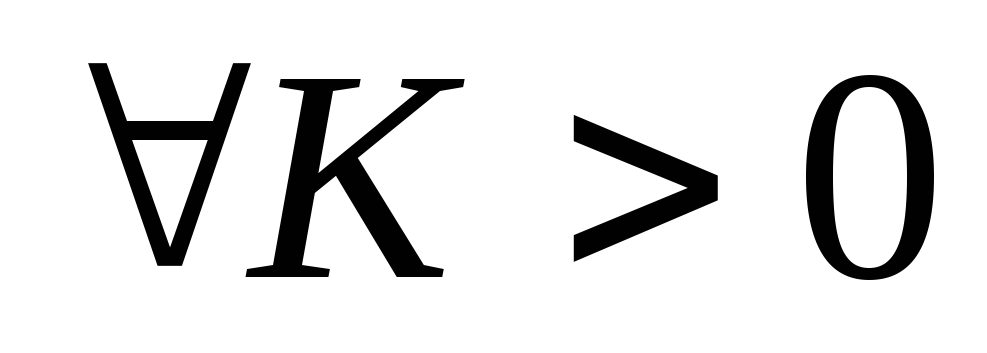 .
Пусть
.
Пусть
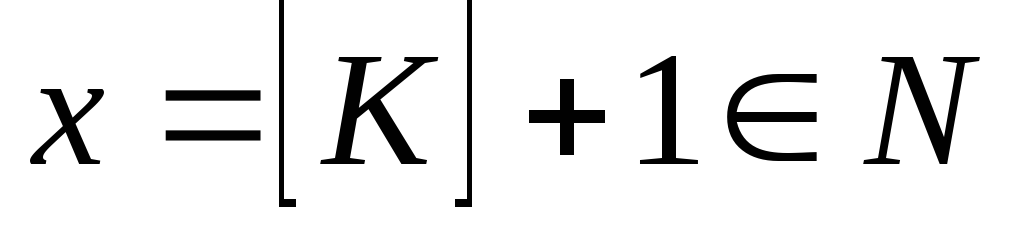 .
. -
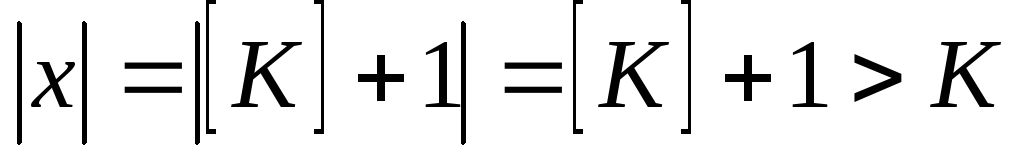 ,
т. к.
,
т. к.
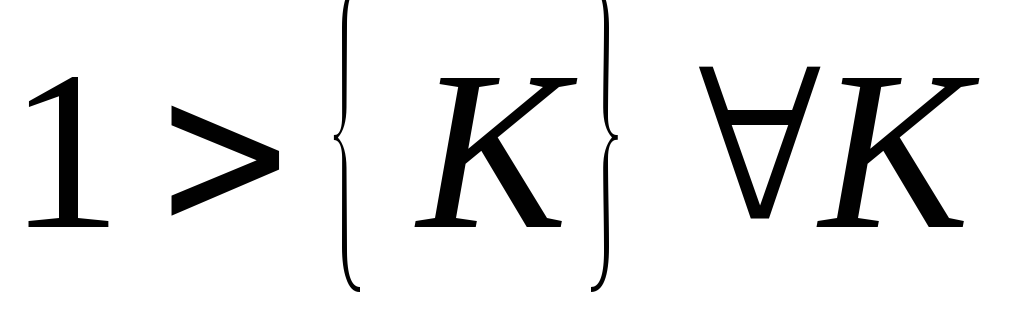 .
.
ч. т. д.
Определение 4.
Наименьшая из всех верхних граней множества А называется его точной верхней гранью и обозначается supA.
Определение 5.
Наибольшая из всех нижних граней множества А называется его точной нижней гранью и обозначается infA.
Определение 4’.
Число М называется точной верхней гранью множества А, если
1.
![]() ;
;
2.
![]() .
.
Определение 5’.
Число m называется точной нижней гранью множества А, если
1.
![]() ;
;
2.
![]() .
.
Доказательство.
Докажем, что
определение 4 и 4’ эквивалентны, т.е.
![]()
![]()
![]()
![]() .
.
Пусть М=supA
– наименьшая из верхних граней множества
А. Следовательно M
– верхняя грань, т. е.
![]() (доказано св-во 1. опр. 4’).
(доказано св-во 1. опр. 4’).
Докажем от
противного, т. е. пусть
![]() число
число
![]() – верхняя грань, причём
– верхняя грань, причём
![]() ,
т. к.
,
т. к.
![]() (доказано св-во 2.
опр. 4’)
(доказано св-во 2.
опр. 4’)![]() М
– наименьшая верхняя грань множества
А.
М
– наименьшая верхняя грань множества
А.
Из свойства 1
следует, что М – верхняя грань. Пусть М
– не наименьшая верхняя грань множества
А
![]() ,
причём М’ – тоже верхняя грань.
,
причём М’ – тоже верхняя грань.
Пусть
![]() .
По свойству 2 для
.
По свойству 2 для
![]() M’
– не верхняя грань множества А. Получили
противоречие.
M’
– не верхняя грань множества А. Получили
противоречие.
Т. к. по нашим предположениям M’ – верхняя грань, что оказалось неверным, то М – наименьшая верхняя грань.
ч. т. д.
Теорема 1.
Всякое непустое, ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.
Доказательство.
Пусть А – непустое,
ограниченное сверху множество
![]() хотя бы одна верхняя грань. Пусть Y
– множество всех верхних граней множества
А (
хотя бы одна верхняя грань. Пусть Y
– множество всех верхних граней множества
А (![]() ø).
ø).
![]() .
Т. о.
.
Т. о.
![]() ø
и
ø
и
![]() ø.
ø.
![]() по свойству
непрерывности действительных чисел
по свойству
непрерывности действительных чисел
![]() ,
отсюда
,
отсюда
![]() – верхняя грань,
т. е.
– верхняя грань,
т. е.
![]()
![]() – наименьшая
верхняя грань, т. е.
– наименьшая
верхняя грань, т. е.
![]() .
.
ч. т. д.
Лекция № 3. Числовая последовательность. Предел последовательности.
Определение 1.
Если каждому
натуральному числу n
ставится в соответствие по некоторому
закону некоторое вещественное число
![]() ,
то множество занумерованных чисел
,
то множество занумерованных чисел
![]() называется числовой последовательностью
и обозначается
называется числовой последовательностью
и обозначается
![]() .
.
Определение 2.
Число a
называется
пределом последовательности
![]() ,
если
,
если
![]() .
В этом случае обозначаем
.
В этом случае обозначаем
![]() .
.
Определение 3.
Если последовательность имеет конечный предел, то она называется сходящейся.
Определение 4.
Последовательность
![]() называется бесконечно малой, если её
предел равен нулю, т. е.
называется бесконечно малой, если её
предел равен нулю, т. е.
![]() .
.
Теорема 1.
Пусть
![]() и
и
![]() – бесконечно малые последовательности,
тогда
– бесконечно малые последовательности,
тогда
-
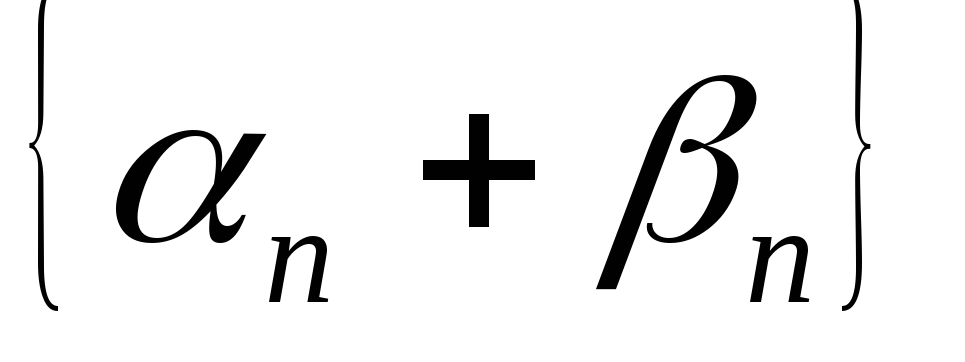 – бесконечно
малая последовательность;
– бесконечно
малая последовательность; -
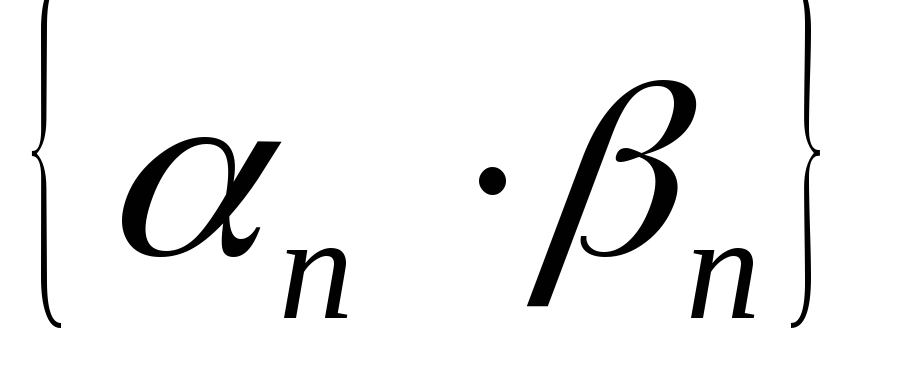 – бесконечно
малая последовательность;
– бесконечно
малая последовательность;
Доказательство.
-
Докажем, что если
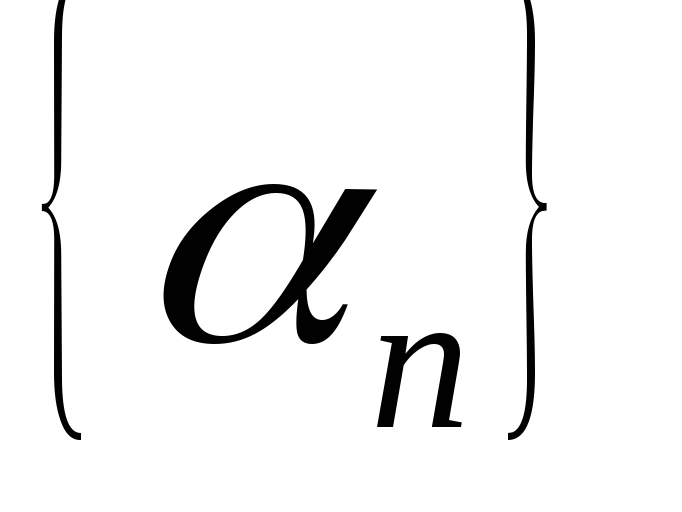 и
и
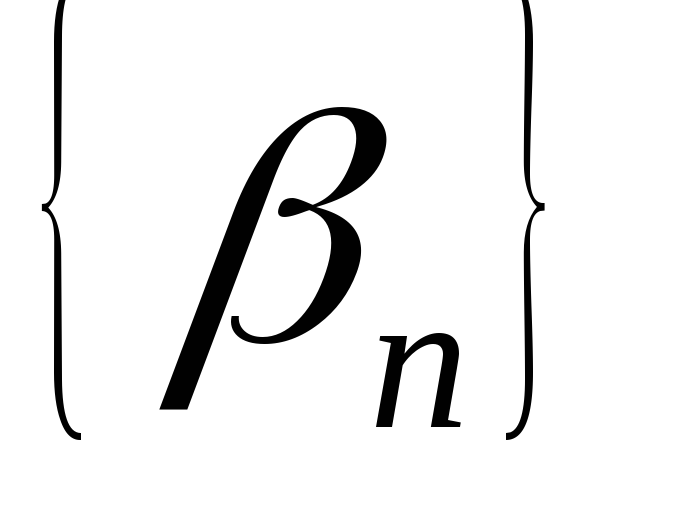 – бесконечно малые последовательности,
тогда и
– бесконечно малые последовательности,
тогда и
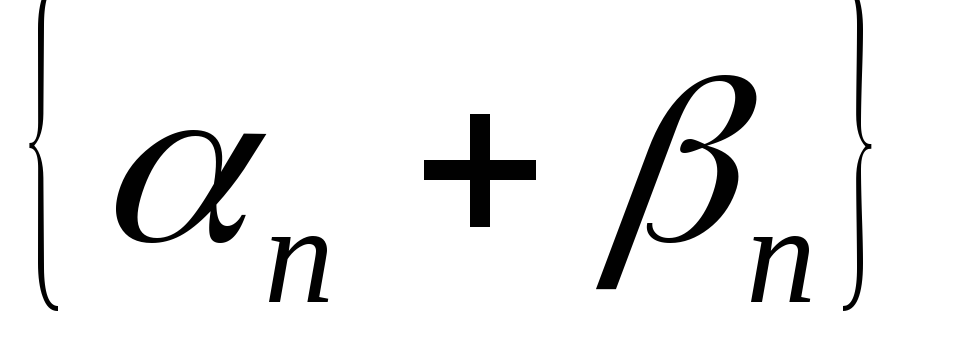 бесконечно малая последовательность.
бесконечно малая последовательность.
Нужно доказать,
что
![]() .
Фиксируем
.
Фиксируем
![]() и обозначим его
и обозначим его
![]() .
.
![]() – бесконечно малая
последовательность
– бесконечно малая
последовательность![]() .
В частности для
.
В частности для
![]() .
.
![]() – бесконечно малая
последовательность
– бесконечно малая
последовательность![]() .
В частности для
.
В частности для
![]() .
.
Пусть
![]()
![]()
![]()
![]() – бесконечно малая последовательность.
– бесконечно малая последовательность.
-
Докажем, что если
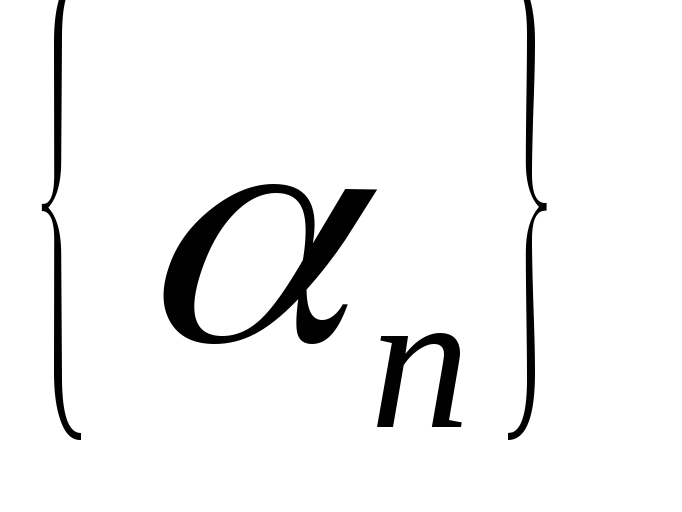 и
и
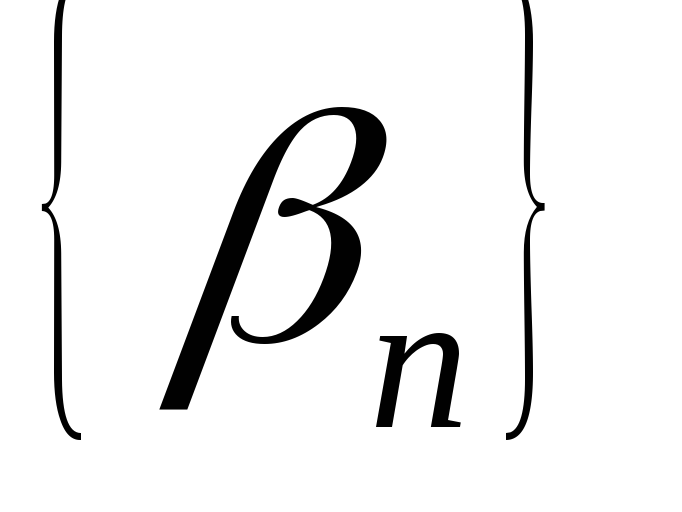 – бесконечно малые последовательности,
тогда и
– бесконечно малые последовательности,
тогда и
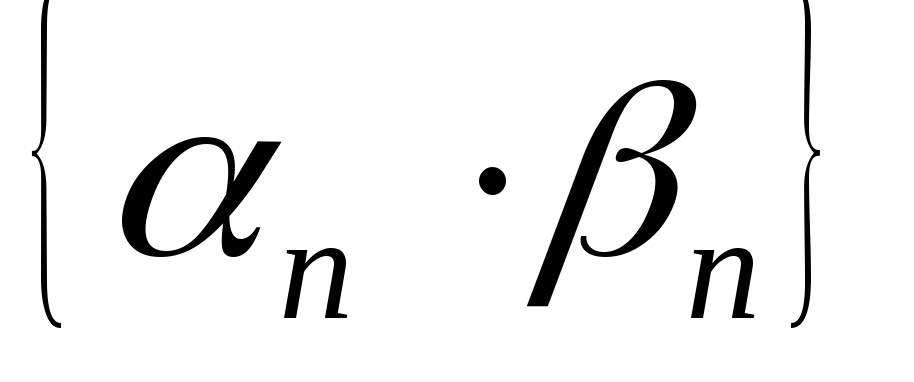 бесконечно малая последовательность.
бесконечно малая последовательность.
Нужно доказать,
что
![]() .
Фиксируем
.
Фиксируем
![]() и обозначим его
и обозначим его
![]() .
.
![]() – бесконечно малая
последовательность
– бесконечно малая
последовательность![]() .
В частности для
.
В частности для
![]() .
.
![]() – бесконечно малая
последовательность
– бесконечно малая
последовательность![]() .
В частности для
.
В частности для
![]() .
.
Пусть
![]()
![]()
![]()
![]() – бесконечно малая последовательность.
– бесконечно малая последовательность.
ч. т. д.
Следствия из теоремы 1.
-
Сумма любого конечного фиксированного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
-
Произведение любого конечного фиксированного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 2.
Пусть
![]() – бесконечно малая последовательность.
Пусть
– бесконечно малая последовательность.
Пусть
![]() – ограниченная последовательность.
Тогда
– ограниченная последовательность.
Тогда
![]() тоже бесконечно малая последовательность.
тоже бесконечно малая последовательность.
Доказательство.
![]() – ограниченная
последовательность
– ограниченная
последовательность
![]() .
.
Фиксируем
![]() .
.
![]() – бесконечно малая последовательность
– бесконечно малая последовательность
![]() .
Следовательно
.
Следовательно
![]() – бесконечно малая последовательность.
– бесконечно малая последовательность.
ч. т. д.
Следствие из теоремы 2.
Пусть
![]() – бесконечно малая последовательность.
Тогда для
– бесконечно малая последовательность.
Тогда для
![]() последовательность
последовательность
![]() тоже бесконечно малая.
тоже бесконечно малая.
Доказательство.
![]() – ограниченная
последовательность
– ограниченная
последовательность
![]()
![]() – бесконечно малая последовательность.
– бесконечно малая последовательность.
ч. т. д.
Определение 5.
Последовательность
![]() называется бесконечно большой, если
называется бесконечно большой, если
![]() .
В этом случае обозначаем
.
В этом случае обозначаем
![]() .
.
Теорема 2. …
Лекция № 5.
Монотонные последовательности. Число
![]() .
.
Определение 1.
Последовательность
![]() называется монотонно возрастающей,
если
называется монотонно возрастающей,
если
![]() .
.
Определение 2.
Последовательность
![]() называется монотонно неубывающей, если
называется монотонно неубывающей, если
![]() .
.
Замечание.
Всякая возрастающая последовательность является неубывающей, однако неубывающая последовательность может не быть возрастающей.
Определение 3.
Последовательность
![]() называется монотонно убывающей, если
называется монотонно убывающей, если
![]() .
.
Определение 4.
Последовательность
![]() называется монотонно невозрастающей,
если
называется монотонно невозрастающей,
если
![]() .
.
Замечание.
Всякая убывающая последовательность является невозрастающей, однако невозрастающая последовательность может не быть убывающей.
Возрастающие, неубывающие, убывающие и невозрастающие последовательности называются монотонными.
Теорема 1.
Если последовательность монотонно не убывает (не возрастает) и ограничена сверху (снизу), то такая последовательность имеет конечный предел.
Доказательство.
Пусть, например,
последовательность
![]() монотонно не убывает и ограничена
сверху.
монотонно не убывает и ограничена
сверху.
![]() ограничена сверху
ограничена сверху
![]()
![]() .
.
![]() не убывает
не убывает
![]() .
.
Таким образом
![]()
ч. т. д.
Замечание.
Из доказательства теоремы видно, что
-
если
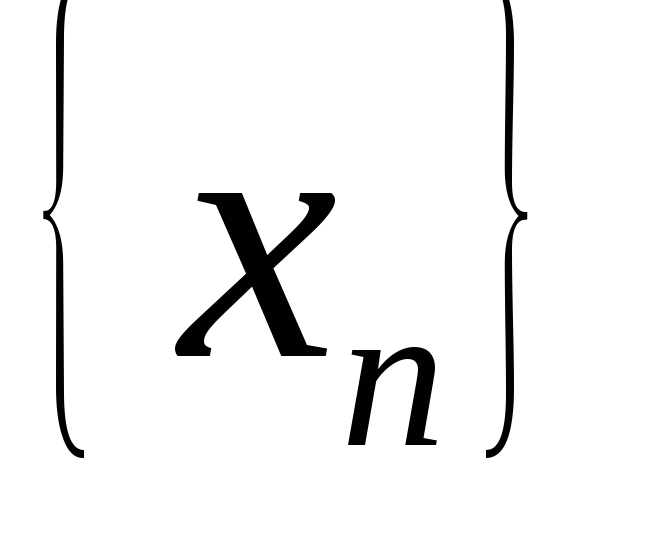 не убывает и ограничена сверху, то
не убывает и ограничена сверху, то
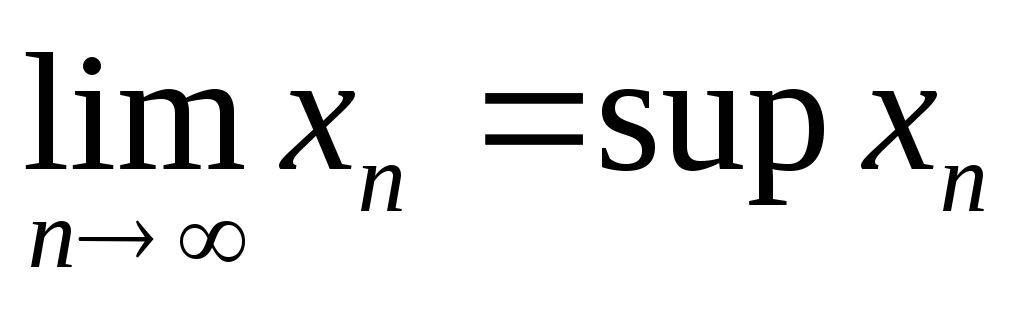 ;
; -
если
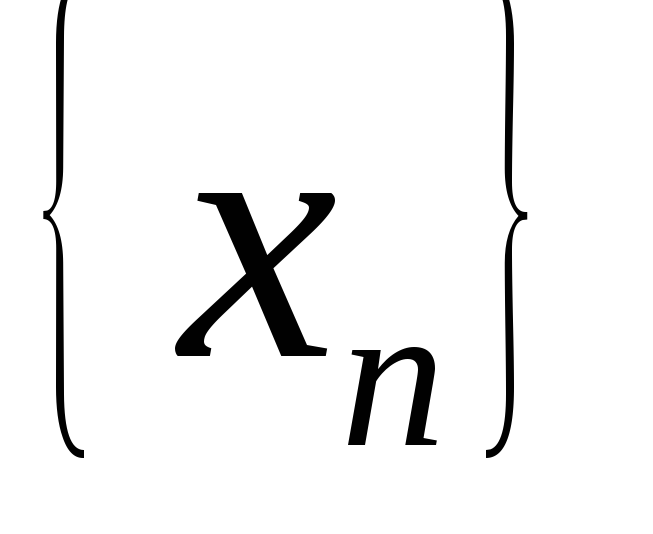 не возрастает и ограничена снизу, то
не возрастает и ограничена снизу, то
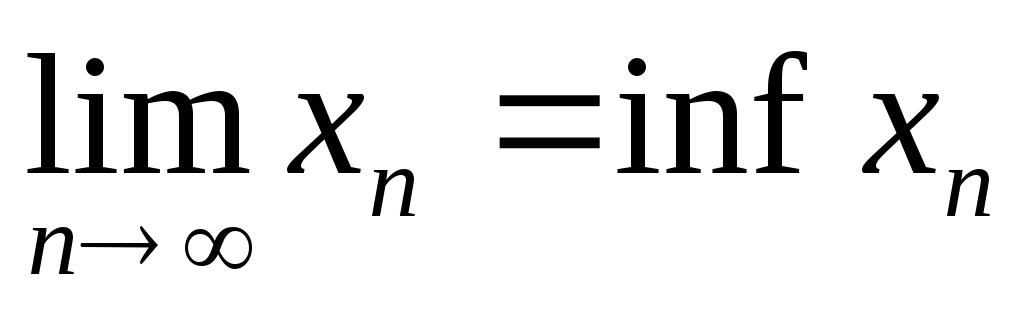 .
.
Теорема.
Пусть
![]() и
и
![]() – бесконечно малые последовательности,
тогда
– бесконечно малые последовательности,
тогда
-
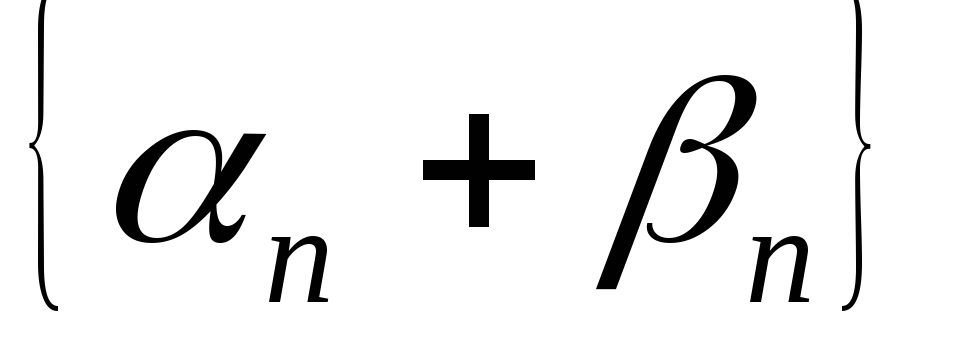 – бесконечно малая последовательность;
– бесконечно малая последовательность; -
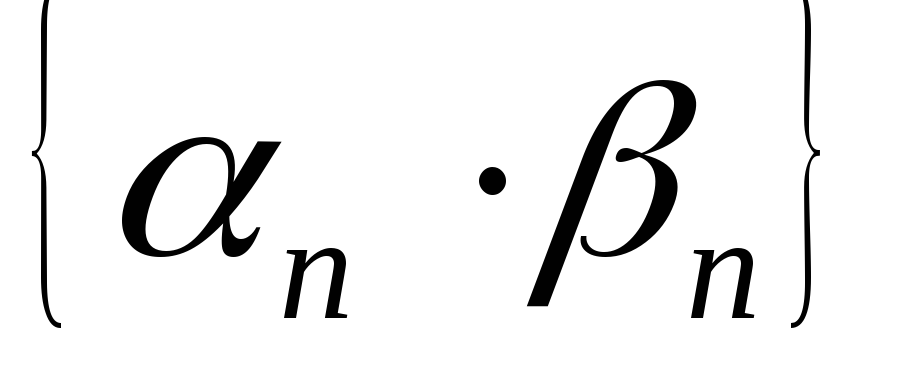 – бесконечно малая последовательность;
– бесконечно малая последовательность;
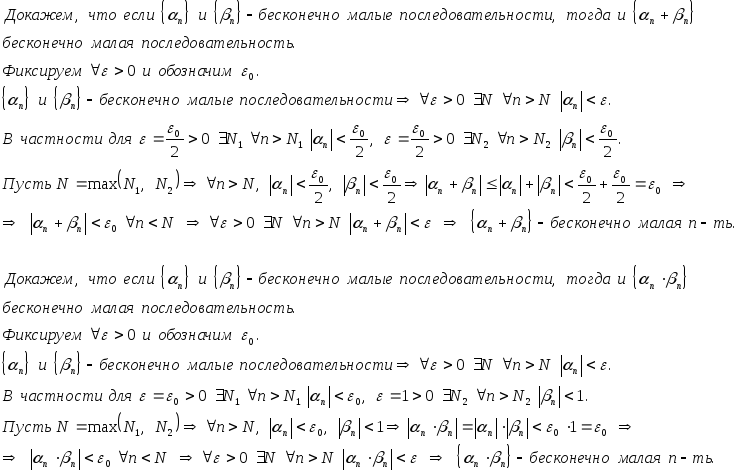
Следствия из теоремы.
-
Сумма любого конечного фиксированного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
-
Произведение любого конечного фиксированного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
