Нижняя и верхняя цены игры. Принцип минимакса.

Итак, рассмотрим матричную игру с платежной матрицей

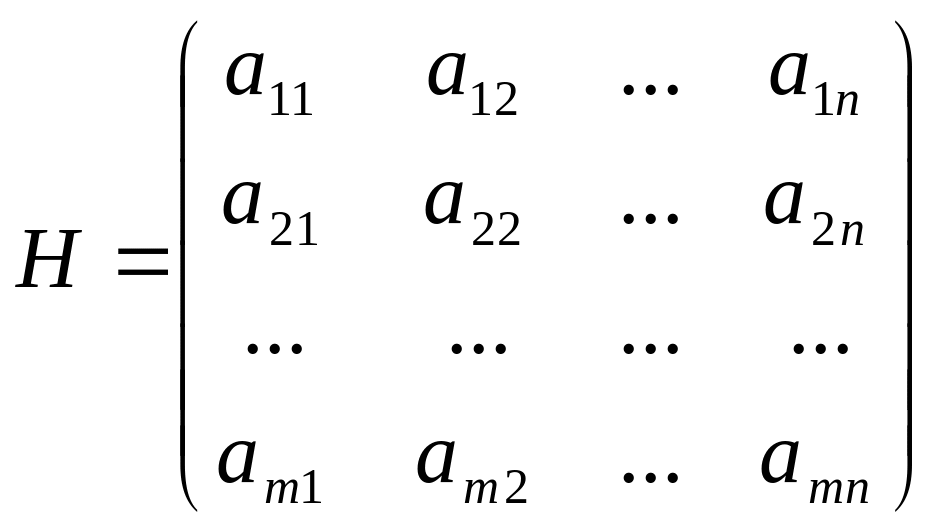(2)

Где i-я строка соответствует А_i-й стратегии игрока А;

j-й столбец соответствует В_j-й стратегии игрока В.

Пусть игрок А выбирает некоторую стратегию А_i, тогда в наихудшем случае (например, если выбор станет известен игроку В) он получит выигрыш равный . Предвидя эту возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный в каждой стратегии выигрыш . Таким образом, . Величина называется нижней ценой игры ( – это гарантированный выигрыш игрока А).

Очевидно, находится в одной из строк матрицы Н, пусть в i₀, тогда стратегия называется максиминной.

Итак, если игрок А будет придерживаться максиминной стратегии, то ему при любом поведении игрока В гарантируется выигрыш, во всяком случае не меньше .

С другой стороны, противник – игрок В, заинтересован в том, чтобы обратить выигрыш игрока А в минимум, поэтому он должен пересмотреть каждую свою стратегию с точки зрения максимального выигрыша игроком А при этой стратегии. Другими словами, при выборе некоторой стратегии B_j он должен исходить из максимального проигрыша в этой стратегии, равного , и найти такую стратегию, при которой этот проигрыш будет наименьшим, то есть не более чем .

Величина называется верхней ценой игры, а соответствующая ему стратегия – минимаксной.

Принцип осторожности, диктующий игрокам выбор стратегий максиминной или минимаксной соответственно, в теории игр именуют принципом минимакса, а сами стратеги максиминные и минимаксные – общим термином минимаксные стратегии.

Рассмотрим пример нахождения и .

Пусть игра задана матрицей

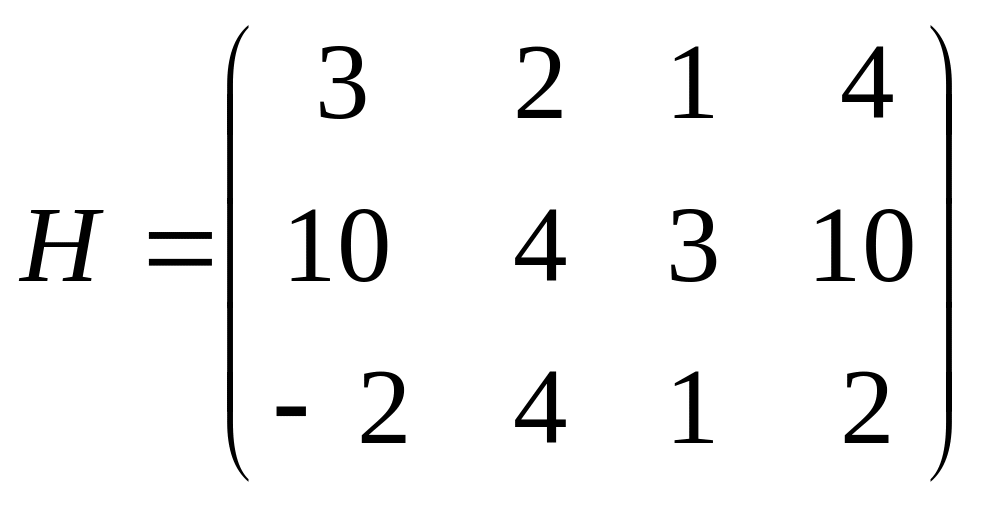
Определим нижнюю и верхнюю цены игры.

Выпишем для каждой строки справа от матрицы , а снизу каждого столбца. Тогда получим:

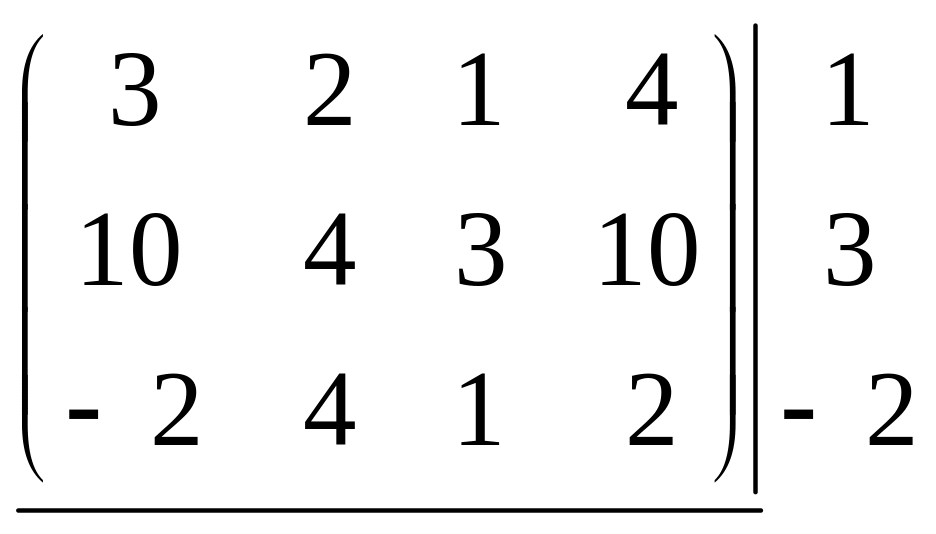
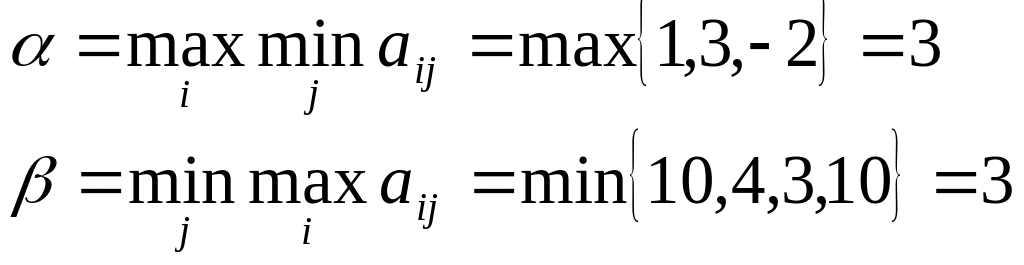
10 4 3 10

В этом примере нижняя и верхняя цены игры совпадают:

Вполне определённые игры.

Вполне определённая игра является наиболее простым случаем матричной игры. Вполне определённой игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство:

(3)

При этом называется ценой игры, элемента соответствующий равенству, называют седловой точкой.

Простота решения игры с седловой точкой заключается в том, что оптимальные стратегии обоих игроков находятся сразу. Для игрока А это стратегия для игрока В – . Причём, такое решение обладает свойством устойчивости в том смысле, что если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться не выгодным для него.

Действительно, пусть игрок А выбрал оптимальную стратегию соответствующую , то есть игрок А обеспечивает себе выигрыш , равный одному из элементов строки, причём, элемент в столбце наименьший среди них . И если игрок В выберет j-ю стратегию отличную от , то он проиграет сумму, равную , а игрок А соответственно выиграет её. Аналогичные рассуждения показывают не выгодность стратегии, отличной от оптимальной, для игрока А, когда В придерживается своей оптимальной стратегии.

Решением игры в примере является выбор стратегий игроком и игроком , при этом цена игры V = 3.