
- •Линейное программирование
- •Решение
- •Методика решения задач лп графическим методом
- •Симплекс метод решения задач лп
- •Решение
- •Анализ чувствительности оптимального решения одноиндексных задач лп
- •Методика графического анализа чувствительности оптимального решения
- •1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)
- •Правило № 1
- •Правило № 2
- •Правило № 3
- •Правило № 4
- •Результаты анализа ресурсов задачи
- •Вторая задача анализа на чувствительность
- •Третья задача анализа на чувствительность
- •Правило 5
- •Теории игр.
- •Нижняя и верхняя цены игры. Принцип минимакса.
- •Вполне определённые игры.
- •Игры, не содержащие седловой точки. Смешанные стратегии.
- •Игры, не содержащие седловой точки. Смешанные стратегии.
- •Упрощение игр
- •Упрощение игр
- •Методы решения матричных игр
- •Графическое решение игры два на два.
- •Решение игр . Эквивалентность матричной игры паре двойственных злп
- •Игра .
- •Решение игры .
- •Решение игры .
- •Решение матричных игр .
- •Критерии выбора стратегий при игре с природой
- •Понятие о цене информации
- •Транспортная задача
- •III. Построение сбалансированной транспортной матрицы.
- •Решение
- •Алгоритм решения транспортной задачи методом потенциалов.
- •Формальное правило улучшения плана:
- •Решение
- •Системы массового обслуживания теория Основные параметры систем массового обслуживания
- •Смо с ограниченной очередью ( ).
- •Смо с неограниченной очередью ( ).
- •Системы массового обслуживания без очереди
- •Системы массового обслуживания с неограниченной очередью
- •Решения
- •99.7% Лежат в ± 3σ
- •95.4% Лежат в ± 2σ
- •68,3% Лежат в ±1σ
- •1 Стандартное отклонение
Смо с ограниченной очередью ( ).
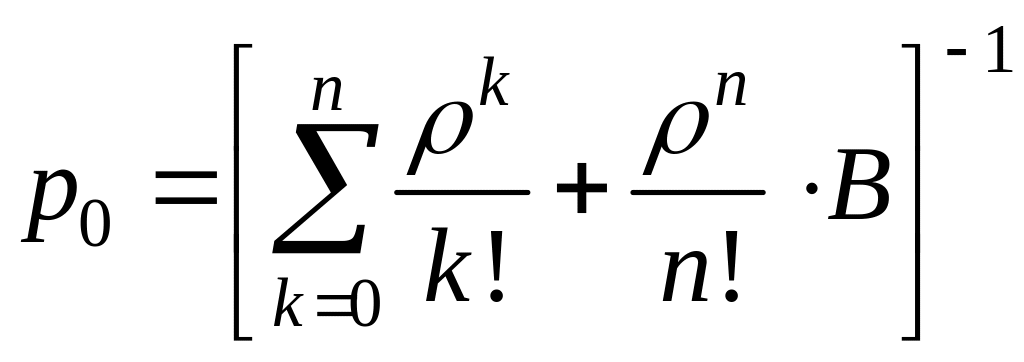 , (9)
, (9)
где
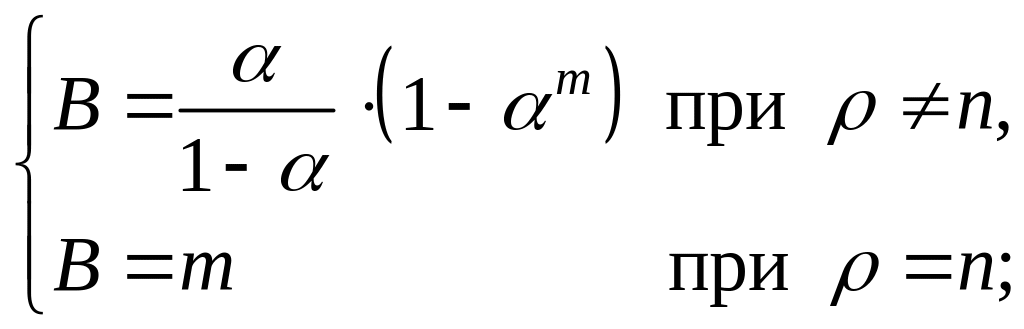 (10)
(10)
![]() , (11)
, (11)
![]() – факториал числа
;
по определению
– факториал числа
;
по определению
![]() .
.
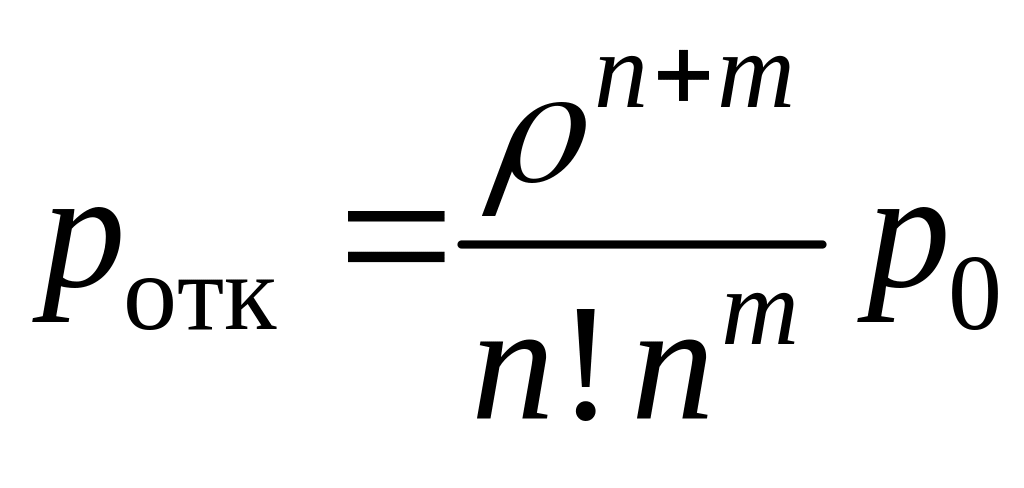 (12)
(12)
(13)
(14)
(15)
(16)  (17)
(17)
где
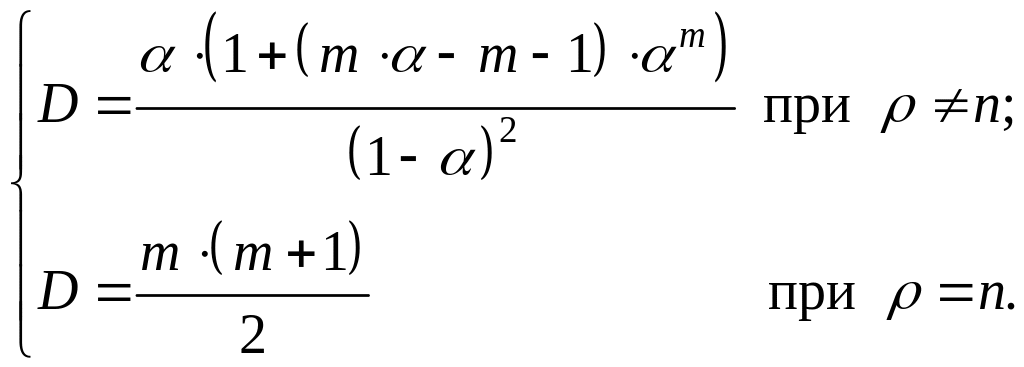 (18)
(18)
(19)
(20)
(21)
Смо с неограниченной очередью ( ).
СМО с неограниченной очередью имеет стационарный режим работы только при условии
![]() .
.
При нарушении этого условия очередь неограниченно возрастает и стационарных значений параметров СМО определить не удается.
При
формулы для основных
параметров данной СМО могут быть получены
из формул предыдущего раздела предельным
переходом
![]() .
.
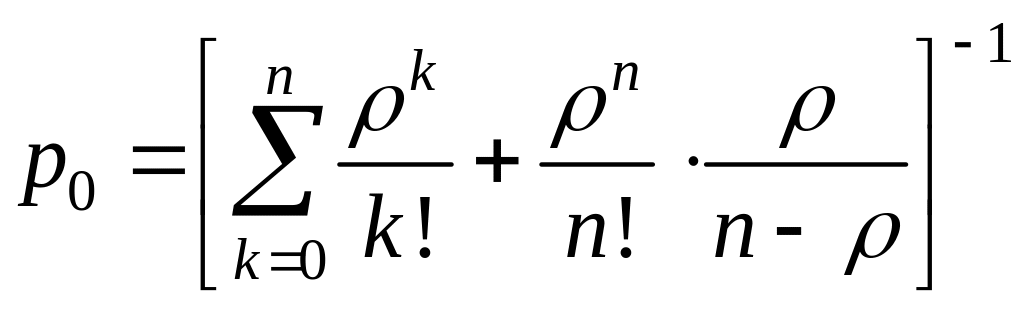 , (22)
, (22)
![]() (23)
(23)
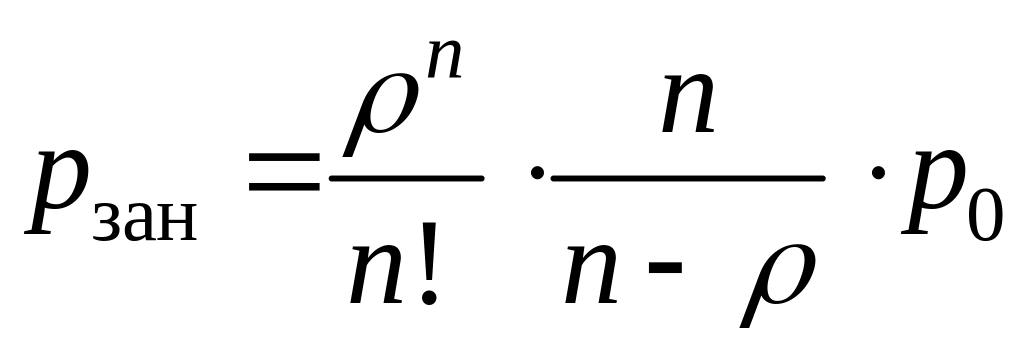 (24)
(24)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
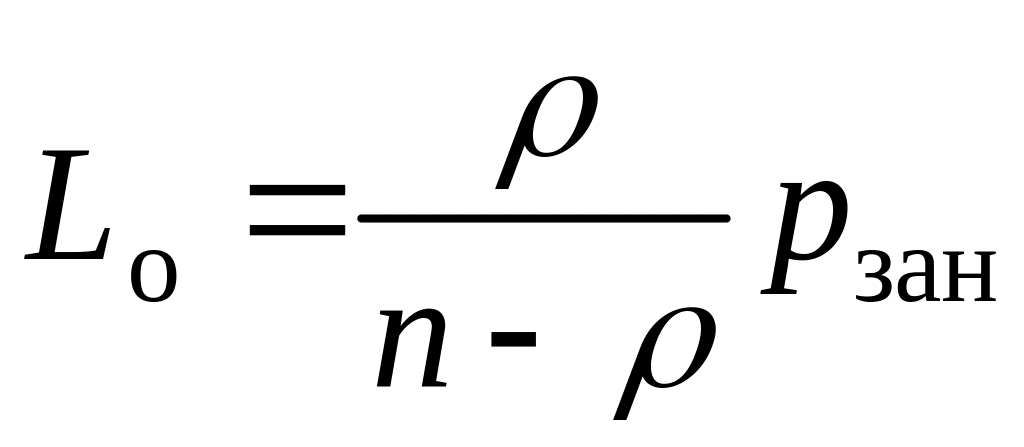 (29)
(29)
(30)
![]() (31)
(31)
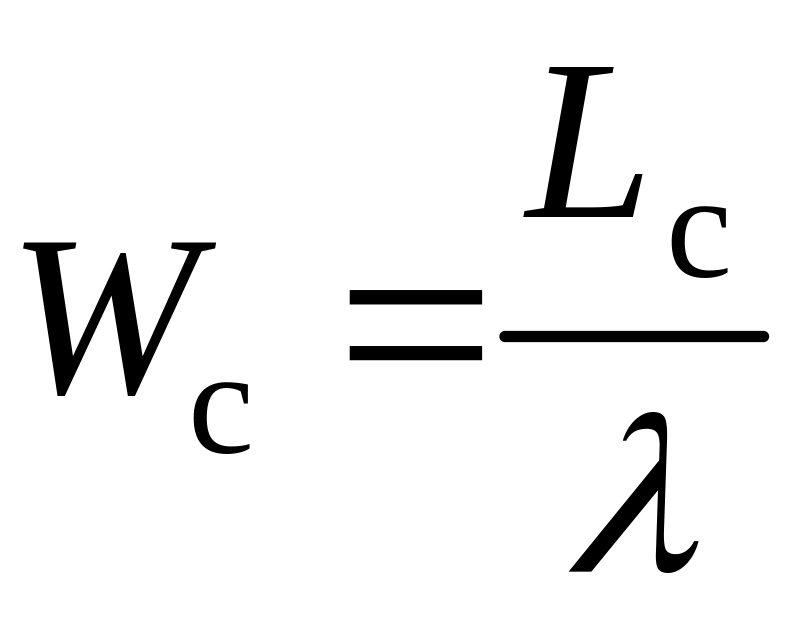 (32)
(32)
СМО без очереди (без ожидания, с отказами) ( ).
Формулы для основных параметров данной СМО могут быть получены из формул для СМО с ограниченной очередью, если в них положить .
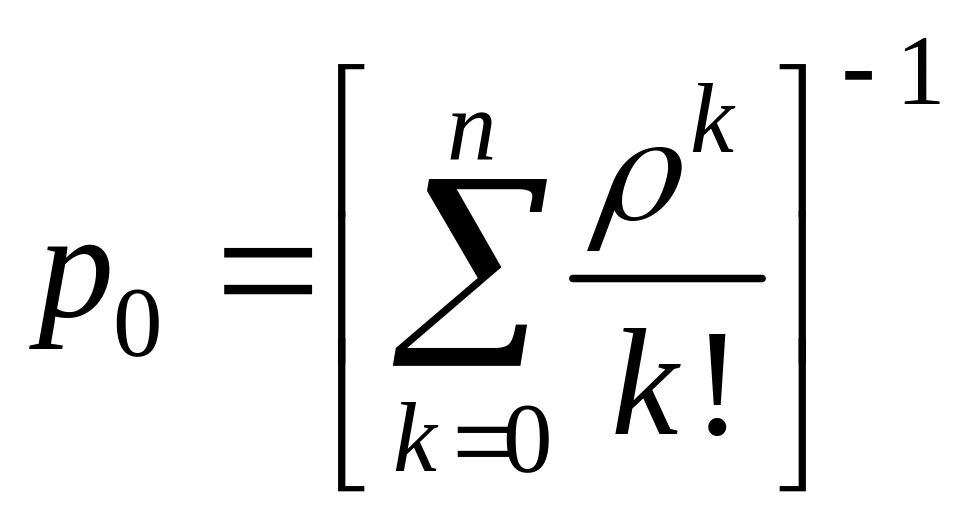 , (33)
, (33)
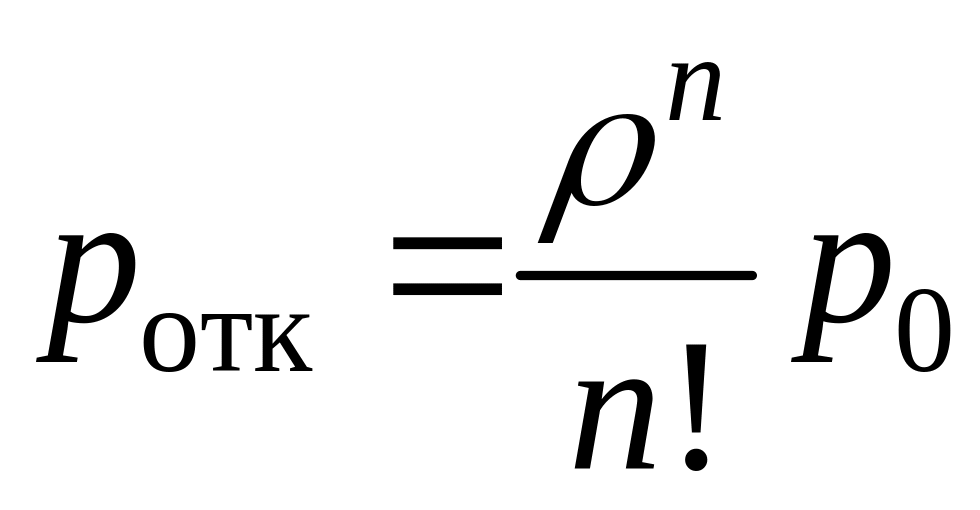 (34)
(34)
![]() (35)
(35)
(36)
![]() (37)
(37)
![]() (38)
(38)
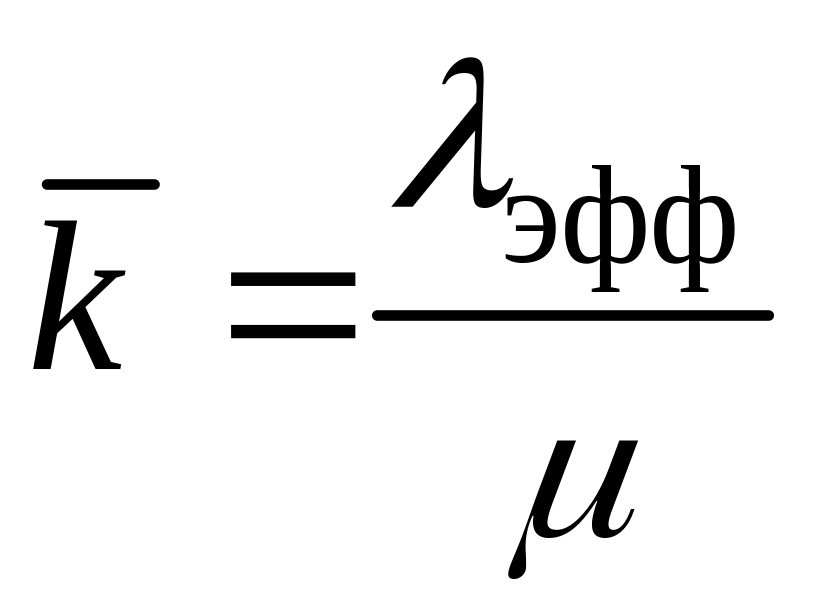 (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
СМО с ограниченным временем пребывания в неограниченной очереди.
 , (44)
, (44)
где
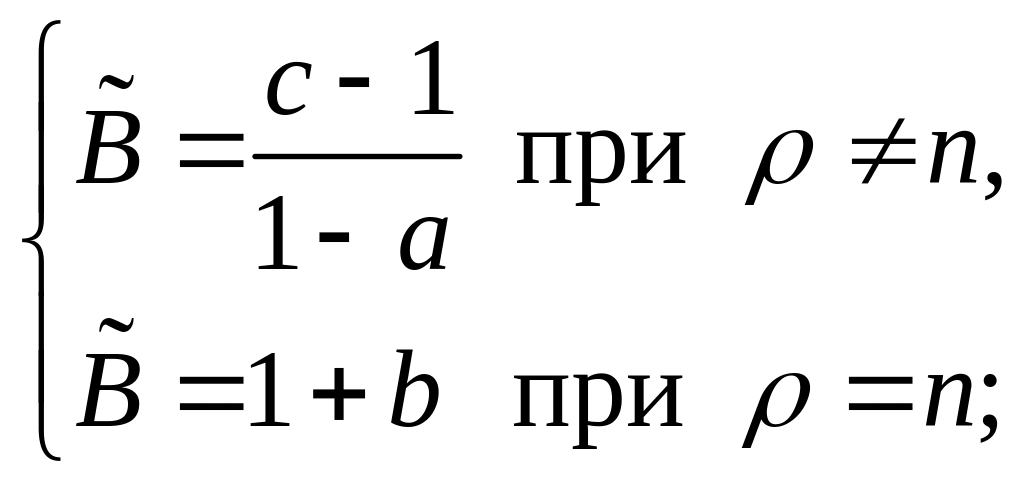 (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
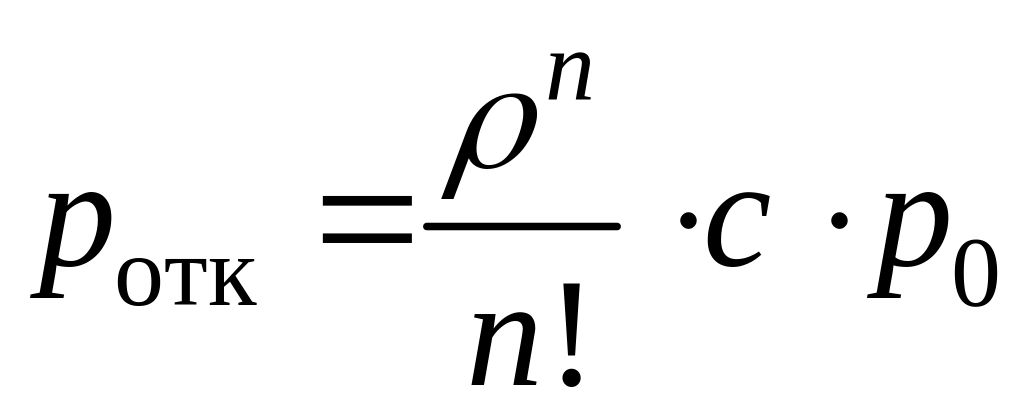 (49)
(49)
(50)
(51)
(52)
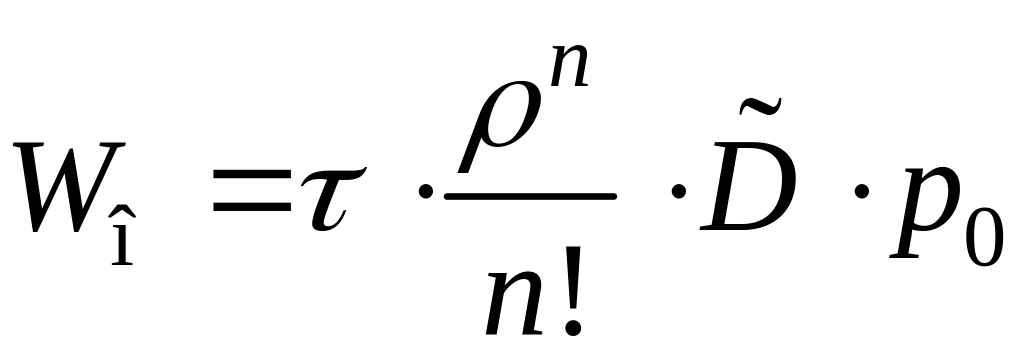 (53)
(53)
где
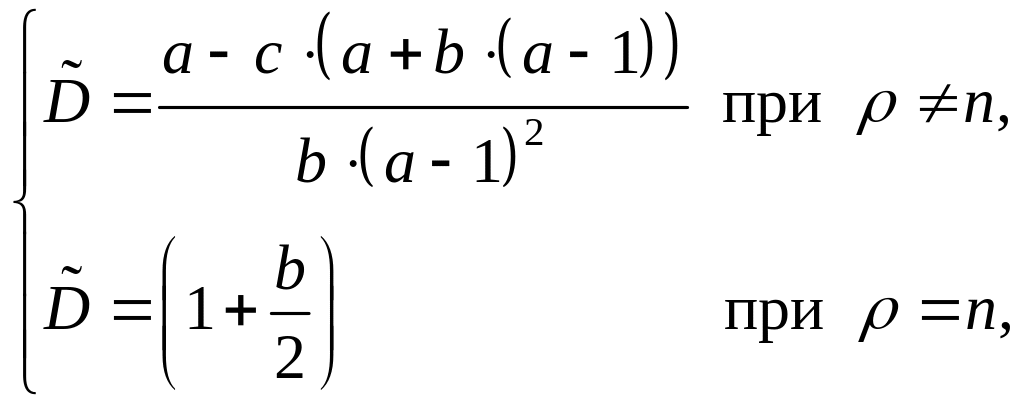 (54)
(54)
Задачи
Системы массового обслуживания с ограниченной очередью
Задача 1.
В пункте круглосуточной охраны 4 бригады. На пульте имеется 6 мест для запоминания поступившего вызова. В услугах бригады нуждается в среднем 4000 клиентов в месяц Бригада тратит на выезд в среднем 40 минут (выезд, проверка, задержание, возвращение).
Найти параметры работы системы. Определить, сколько клиентов будут «ограблены» – получат отказ. Сколько времени «ожидает» приезда бригады грабитель?
Определить, что оптимальнее с точки зрения для интенсификации работы системы, нанять еще одну бригаду или увеличить число мест на пульте до 10?
Задача 2.
На шоссе проверяет скорость патруль ГИБДД, состоящий из двух инспекторов. Инспектор оформляет протокол в среднем 10 минут. Инспекторы останавливают машину, если ожидают оформления не более трех машин. Статистически установлено, что за час на данном участке шоссе пытаются превысить скорость в среднем 70 водителей.
Определить параметры работы системы. Найти процент оштрафованных нарушителей. Каково среднее время, которое тратит водитель в ожидании оформления протокола? Сколько, в среднем, машин ожидает оформления?
Определить, что оптимальнее (с точки зрения наказания нарушителей), оформлять протокол в два раза быстрее или увеличить число инспекторов в два раза?
Системы массового обслуживания без очереди
Задача 3.
В офисе туристической фирмы два многоканальных телефона. По первому, имеющему четыре канала, менеджеры дают информацию о предлагаемых круизах (назовем этих менеджеров и эти телефоны «рекламными»). По второму, с двумя каналами, проводится консультирование клиентов по правилам оформления документов (их назовем «оформительскими»). В час на фирму поступает в среднем 30 звонков с целью получить рекламную информацию и 10 звонков для получения консультации по оформлению. Один рекламный менеджер дает рекламную информацию в среднем за 10 минут, а оформительскую мог бы дать за 30 минут. Менеджер-оформитель отвечает на любой звонок в среднем 15 минут. Заметим, что если все телефоны заняты, то звонок, а следовательно и клиент теряются.
Рассмотреть работу двух раздельных систем массового обслуживания и работу объединенной системы. Найти параметры работы задачи об офисе туристической фирмы. Дать трактовку всем найденным параметрам. Определить, выгодно ли объединение менеджеров.
Задача 4.
В лесу работает 5 лесников. Лесник производит задержание и оформление браконьера в среднем за 10 часов. За день (световой день летом равен 15 часов) пытаются вести незаконную охоту в среднем 9 человек. Очевидно, браконьеры не дожидаются «занятого» лесника. Определить, сколько браконьеров будет наказано, а какой процент окажется непойманными. Что эффективнее, взять лишнего лесника или ускорить работу лесников до 7,5 часов на браконьера?
