Системы массового обслуживания теория Основные параметры систем массового обслуживания

– число каналов обслуживания (мастеров, врачей, барменов и т.п.). Измеряется в «штуках». Например, в парикмахерской работает 4 мастера, значит .

– максимальная длина очереди (максимальное количество мест для ожидания обслуживания). В СМО без очереди ( ) и с неограниченной очередью ( ) этот параметр явно не участвует. Измеряется в «штуках». Например, в парикмахерской есть 3 кресла для ожидания, тогда .

– среднее время обслуживания одной заявки одним каналом (среднее время, которое тратит мастер, врач и т.п. на одного клиента, пациента; среднее время, которое тратится станцией техобслуживания на один автомобиль и т.д.). Измеряется в единицах времени. Пример: парикмахер обслуживает клиента в среднем за 40 минут: мин. Этот параметр зависит только от свойств системы массового обслуживания и не зависит от входящего потока (например, если большинство клиентов уедет в отпуск, скорость работы парикмахера не поменяется).

– интенсивность обслуживания одним каналом (среднее число заявок, которые обслуживает один канал за единицу времени; число заказов, обслуживаемых за единицу времени). Измеряется в «штуках» за единицу времени. Связан со среднем временем обслуживания соотношением:

.

Этот параметр, как и , зависит только от свойств системы массового обслуживания и не зависит от входящего потока. Для нашего примера: интенсивность работы парикмахера клиента за минуту. Важно следить, за какую единицу времени происходит обслуживание. Нужно, чтобы и были отнесены к одной единице времени (день, час, минута и т.п.). Через эту единицу будут выражаться все остальные параметры задачи, зависящие от времени или отражающие средние времена. В примере нужно перевести из клиентов в минуту в клиентов в рабочий день. Так как в рабочем дне 8 часов по 60 минут, то клиентов в день.

– интенсивность внешнего потока (среднее число заявок в единицу времени; число клиентов, пациентов и т.п., обращающихся в единице времени). Измеряется в «штуках» за единицу времени. Пример: за восьмичасовой часовой рабочий день в салон красоты обращается в среднем 50 человек: человек в раб. день. Этот параметр зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, при болезни парикмахера поток клиентов, приходящих на обслуживание, не меняется).

– максимальное время ожидания требованием начала обслуживания (время, после которого портится не обслуженный продукт, уходит нетерпеливый клиент, станивится неактуальным выполнение заказа и т.п.). Измеряется в единицах времени. СМО в этом случае носят название систем массового обслуживания с ограниченным временем ожидания. Необходимо, чтобы время было выражено в тех же единицах, к которым приведены и . Этот параметр, как и параметр , зависит только от свойств входящего потока и не зависит от свойств самой системы массового обслуживания (например, неиспользуемое молоко киснет в течении трех дней вне зависимости от интенсивности работы повара и количества поваров).

Итак, параметры , , и определяются свойствами обслуживающей системы, а параметры и – свойствами входящего потока.

Параметры, которые получим в дальнейшем, определяются взаимодействием обслуживающей системы и потока.

– интенсивность нагрузки. Безразмерная величина. До вычисления параметры и обязательно должны быть приведены к единой единице времени!

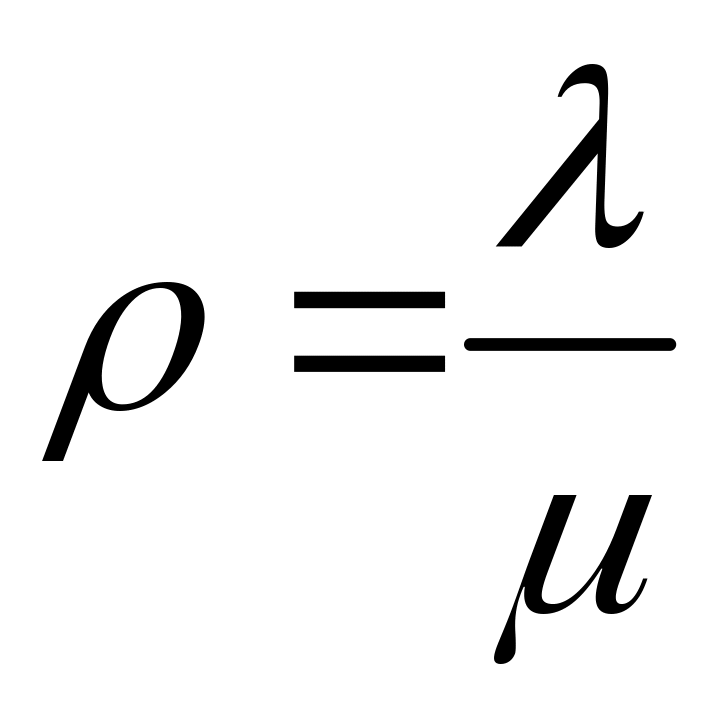(1)

– вероятность того, что занято ровно каналов обслуживания или доля общего времени работы СМО в течении которого заняты ровно каналов. Безразмерная величина, находится в диапазоне от 0 до 1.

– доля времени, когда все каналы свободны. Безразмерная величина, находится в диапазоне от 0 до 1. Является промежуточной величиной расчета всех СМО. Через нее выражаются многие остальные параметры. Безразмерная величина, находится в диапазоне от 0 до 1.

– вероятность того, что все каналы обслуживания заняты (заняты все мастера, врачи и т.д.). Безразмерная величина, находится в диапазоне от 0 до 1. Иначе говоря, это доля времени, в которое поступившая заявка попадает в очередь или получает отказ, если очереди нет или она максимально заполнена.

– вероятность отказа в обслуживании или доля из общего числа требований, которым будет отказано в обслуживании из-за занятости всех каналов и мест ожидания или из-за превышения максимального времени ожидания. Безразмерная величина, находится в диапазоне от 0 до 1.

– вероятность обслуживания или доля из общего числа требований, которые будут обслужены. Безразмерная величина, находится в диапазоне от 0 до 1. Еще одно название – относительная эффективность обслуживания.

(2)

– абсолютная эффективность обслуживания (абсолютная пропускная способность). Количество требований, которые будут обслужены в единицу времени (число обслуженных за день, за час, за минуту заявок, клиентов и т.п.). Измеряется в «штуках».

(3)

– абсолютная эффективность отказа. Количество требований, получивших отказ в обслуживании в единицу времени (число клиентов, заявок и т.п., которым будет отказано в течении дня, часа, минуты). Измеряется в «штуках».

(4)

– среднее число занятых каналов обслуживания (число работающих мастеров, занятых телефонов и т.п.). Измеряется в «штуках».

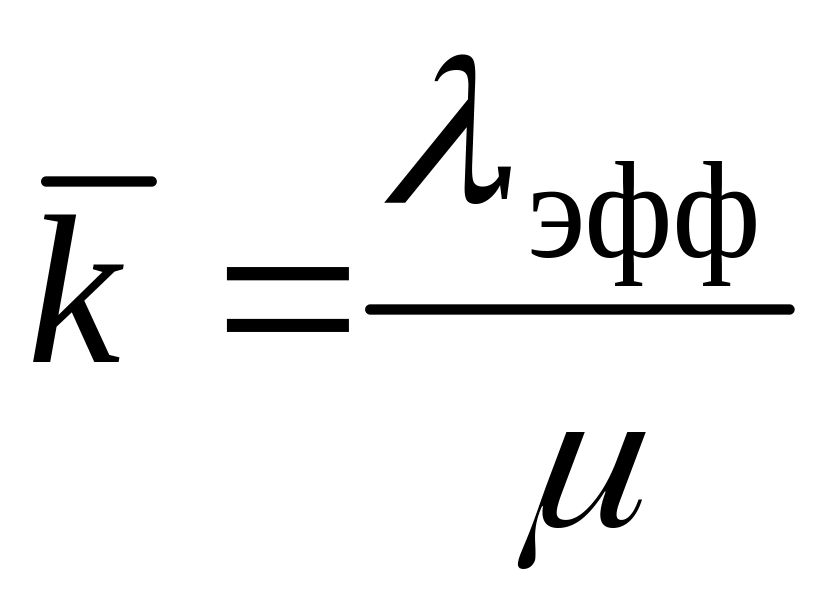(5)

– средняя длина очереди (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди). Измеряется в «штуках».

– среднее количество требований в системе (среднее число клиентов, заявок, ожидающих начала обслуживания в очереди и обслуживаемых в СМО). Измеряется в «штуках».

(6)

– среднее время, которое проводит требование в очереди (общее время, которое, в среднем, один клиент проводит в ожидании начала обслуживания и во время обслуживания). Измеряется в единицах времени. Иногда обозначается или .

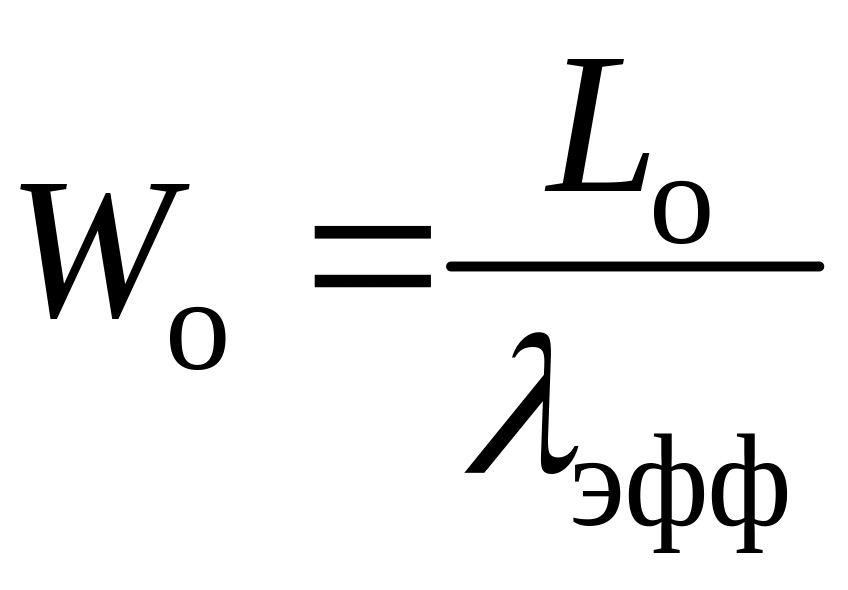(7)

– среднее время, которое проводит требование в системе (время, которое, в среднем, один клиент проводит в ожидании начала обслуживания). Измеряется в единицах времени. Иногда обозначается или .

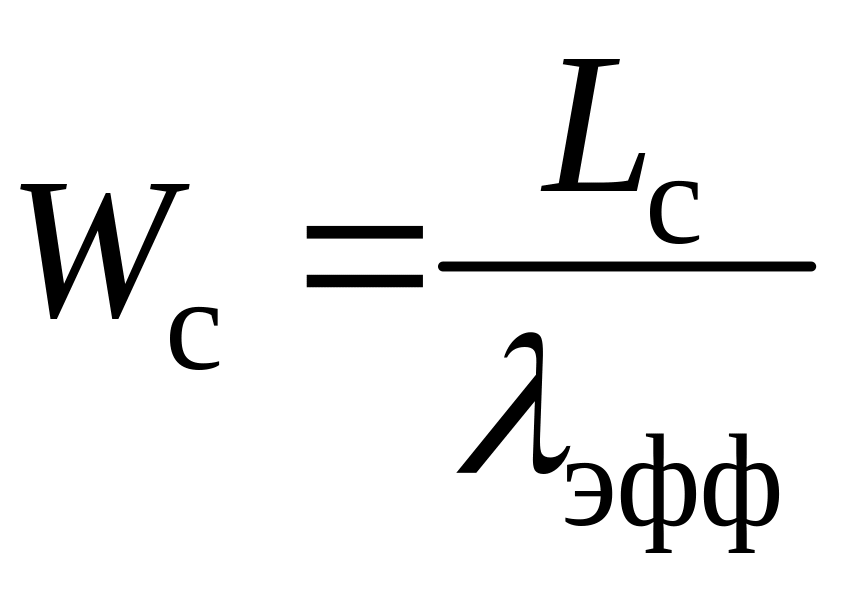(8)

Заметим, что в результате расчета по формулам, и будут выражены в той же временной единице, к которой приведены и . Иногда это не удобно для интерпретации решения (например, среднее время ожидания равно 0,03125 раб. дня). В этом случае необходимо перевести эти параметры в другую единицу измерения времени:

Например:

Важно понимать, что все эти величины носят средне статистический характер, то есть реализуются «в среднем» при продолжительном времени устойчивой работы системы массового обслуживания.

Формулы определения параметров различаются для разных типов СМО (связи между параметрами, определенные по формулам (1)–(8) остаются справедливыми для всех СМО). Приведем полный набор формул для СМО четырех типов. Для удобства повторим формулы (1)–(8) в каждом случае.