Решение игры .

Пусть игра задана матрицей

.

Строим прямые, соответствующие стратегиям игрока В рис. 2.3.

Ломаная соответствует нижней границе выигрыша, точка К на ней даёт решение игры: , , .

В данном случае оптимальная стратегия противника получается применением смеси двух полезных стратегий и , пересекающихся в точке К. Стратегия является заведомо выгодной при оптимальных стратегиях.

, .

0

0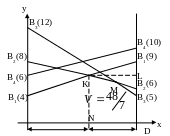

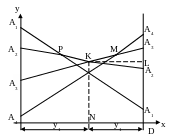
рис. 2.3. Иллюстрация решения игры рис. 2.4. Иллюстрация решения игры

Решение игры .

Аналогично может быть решена игра с матрицей , только в этом случае строим верхнюю границу выигрыша и на ней определяем минимум.

Пусть игра задана матрицей

.

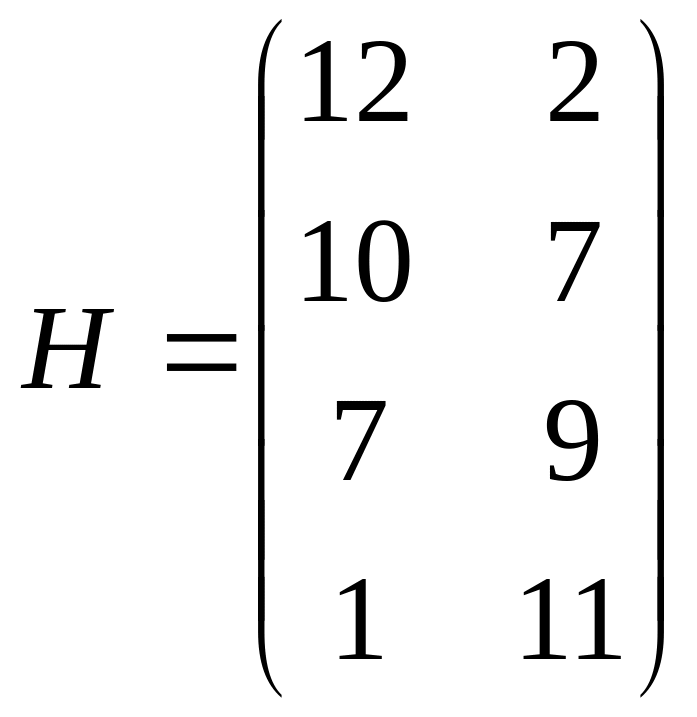Решение задачи находим для игрока В рис. 2.4.

Ломаная изображает верхнюю границу выигрыша игрока А, на ней ищется точка К с минимальной ординатой, которая и есть цена игры , , .

Оптимальными стратегиями для игрока А являются вторая и третья. При этом

, .

Матрица оптимальных стратегий имеет вид . Тогда решение можно найти по формулам (2.4), (2.5), (2.6), (2.8) и (2.9).

Следовательно, решение игры таково:

, , .

Решение матричных игр .

При решении произвольной конечной игры размера рекомендуется придерживаться следующей схемы:

1. Исключить из платёжной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).

2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена игры совпадает с верхней (нижней) ценой.

3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера рекомендуется симплексный метод, а для игр размером , , следует руководствоваться выводами предыдущих пунктов.

Пример (п.2.3)

Магазин может завести в различных пропорциях товары четырёх типов . Их реализация и прибыль магазина зависят от вида товара и состояния спроса.

Предполагается, что спрос может иметь пять состояний и не прогнозируется. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантируемой прибыли, при следующей матрице прибыли табл. 2.2.

Таблица 2.2

Матрица прибыли

Тип товара	Спрос
	В1	В2	В3	В4	В5
А1 А2 А3 А4	200 300 400 700	400 400 500 300	600 600 600 500	400 500 500 200	700 800 800 100

Будем рассматривать возникшую ситуацию как игровую. Сторона А стремится увеличить прибыль, а потому для неё стратегия заведомо выгодна по сравнению со стратегией . Точно так же стратегия уступает стратегии , и исходные данные упрощаются табл. 2.3.

Для игрока В естественным является выбор стратегии с большим спросом. Поэтому стратегия менее выгодна, чем стратегия , в свою очередь, стратегия невыгодна по сравнению со стратегией .

Таблица 2.3 Матрица игры заданная таблицей Таблица 2.4 Матрица игры заданная таблицей

В А В1 В2 В3 В4 В5 А3 А4 400 700 500 300 600 500 500 200 800 100

В А В1 В3 В5 А3 А4 400 700 600 500 800 100

Следовательно, имеет смысл анализировать игру , заданную табл. 1.4. Решение этой матрицы даёт оптимальную стратегию завоза товаров , т.е. нужно завести товара третьего типа и товара четвёртого типа, а товары первого и второго типов не завозить, при этом средняя гарантированная прибыль (цена игры) .

Пример (п.2.4)

Предполагается оснастить цех новой технологической линией. Промышленность выпускает три типа линий. На каждой из линий можно изготовлять пять различных видов изделий. Учитывая расходы сырья, трудоёмкость, спрос и др., составлена матрица предполагаемой прибыли

.

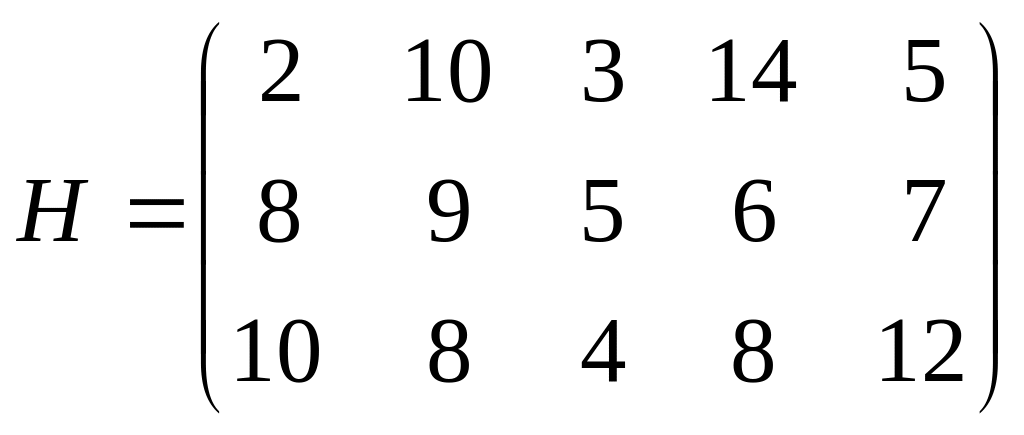Нужно выбрать тип технологической линии, при которой прибыль будет наибольшей.

Так как , то игра имеет седловую точку и задача разрешима в чистых стратегиях. Выбирая второй тип технологической линии, будет достигнута наибольшая прибыль не меньше пяти.