1.Сколько технологических способов (способов переработки сырья в продукт) задано?

Задано четыре технологических способов, т.к. задано четыре связи сырье-продукт.

2. По каждому технологическому способу составьте единичные и объемные векторы «затраты-выпуск» (сырье-продукт).

Единичные векторы «сырье-продукт» (На первом месте всегда сырье):

первым технологическим способом для производства 1 единицы продукции вида А можем использовать 2 единицы сырья 1, 1 единицу сырья 2, 3 единицы сырья 3.

вторым технологическим способом для производства 1 единицы продукции вида Б можем использовать 1 единицу сырья 1, 5 единиц сырья 2.

третьим технологическим способом для производства 1 единицы продукции вида В можем использовать 1/2 единиц сырья 1, 3 единиц сырья 2, 6 единицу сырья 3.

четвертым технологическим способом для производства 1 единицы продукции вида Г можем использовать 4 единицы сырья 1, 1 единицу сырья 3.

Объемные векторы «сырье-продукт» (На первом месте всегда сырье):

1. 2400/2=1200, 1200/1=1200, 3000/3=1000 - выбираем наименьшее число, т.к. у нас ограничение по запасу сырья (меньше можно, больше – невозможно, т.к. у нас в запасе определенное количество сырья).

первым технологическим способом можно изготовить 1000 единиц продукции вида А, при этом будет затрачено 2000 единиц сырья 1, 1000 единиц сырья 2, 3000 единиц сырья 3. Третий вид сырья будет выработан полностью.

2. 2400/1=2400, 1200/5=240 - выбираем наименьшее число, т.к. у нас ограничение по запасу сырья.

вторым технологическим способом можно изготовить 240 единиц продукции вида Б, при этом будет затрачено 240 единиц сырья 1, 1200 единиц сырья 2. Второй вид сырья будет выработан полностью.

3. 2400/(1/2)=4800, 1200/3=400, 3000/6=500 - выбираем наименьшее число, т.к. у нас ограничение по запасу сырья.

третьим технологическим способом можно изготовить 400 единиц продукции вида В, при этом будет затрачено 200 единиц сырья 1, 1200 единиц сырья 2, 2400 единиц сырья 3. Второй вид сырья будет выработан полностью.

4. 2400/4=600, 3000/1=3000 - выбираем наименьшее число, т.к. у нас ограничение по запасу сырья.

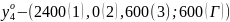четвертым технологическим способом можно изготовить 600 единиц продукции вида Г, при этом будет затрачено 2400 единиц сырья 1, 600 единиц сырья 3. Первый вид сырья будет выработан полностью.

3. Составьте математическую модель (совокупность алгебраических соотношений) планирования выпуска продукции по технологическим способам исходя из условия максимизации прибыли.

Принимаем: [х] – единица продукции (смотрим в шапке таблице)

Совокупность алгебраических соотношений (ни в коем случае не система):

Т.к. у нас цель максимизировать прибыль, то → max.

Т.к. у нас ограничение по запасу сырья (меньше затратить сырья можно, больше – невозможно) выбираем знак ≤.

Задача №5.

В таблице задано количество изделий А и Б, которое может быть изготовлено из каждой единицы сырья, каждым из четырех технологических способов:

Изделие	Выход изделия из единицы сырья				План выпуска
	1	2	3	4
А	2	1	7	4	5574
Б	6	12	2	3	328