
- •Задача № 1. - Оценка уровня качества однородной продукции (товаров и услуг) по нескольким параметрам (4 часа)
- •1.1.Дифференциальный метод оценки уровня качества по нескольким параметрам
- •1.2.Комплексный метод оценки уровня качества по нескольким параметрам
- •Исходные данные для расчета задачи 1.1. По вариантам:
- •Дополнительные исходные данные, необходимые для расчета задачи 1.2. По вариантам:
- •Задача 1.3. Комплексный метод оценки уровня качества продукции с помощью интегрального показателя
- •Задача 2. Оценка качества объектов методом нормализации разнородных показателей и их аддитивного взвешенного свертывания.
- •Задача № 3. – Оценка уровня качества разнородной продукции (товаров и услуг) по нескольким параметрам.
- •3.1. Оценка качества продукции с помощью индекса качества.
- •3.2. Оценка качества продукции с помощью индекса сортности.
- •3.3. Оценка качества продукции с помощью коэффициента дефектности.
- •3.4. Оценка качества продукции с помощью индекса дефектности.
- •Задача № 4. – Оценка затрат на качество.
- •Исходные данные для расчета задачи 4.1. По вариантам:
Задача 2. Оценка качества объектов методом нормализации разнородных показателей и их аддитивного взвешенного свертывания.
В задаче будут приведены исходные данные:
Показатели эффективности работы предприятия общие для всех вариантов;
Значения весовых коэффициентов показателей эффективности работы компаний определяются по варианту (последняя цифра шифра студента).
Требуется определить:
единичные показатели качества относительно базовых;
комплексные показатели качества по формулам среднего геометрического взвешенного, среднего квадратического взвешенного и среднего арифметического взвешенного.
Алгоритм решения:
Определяем какие показатели исследуемого объекта относятся к положительным или отрицательным. К первой группе относятся те показатели, увеличение численного значения которых соответствует улучшению качества. Ко второй группе относятся те показатели, увеличение численного значения которых приводит к снижению качества;
Выделить в каждом столбце j базовые (эталонные) максимальные по абсолютной величине показатели
 или
или
 ;
;Нормализовать показатели путем деления каждого из них на базовый, используя формулы:
– для положительных показателей:
![]() ,
,
где i – номер исследуемого объекта (номер строки);
j – номер показателя (номер столбца);
– для отрицательных показателей:
![]() .
.
Рассчитать комплексный показатель качества исследуемого объекта
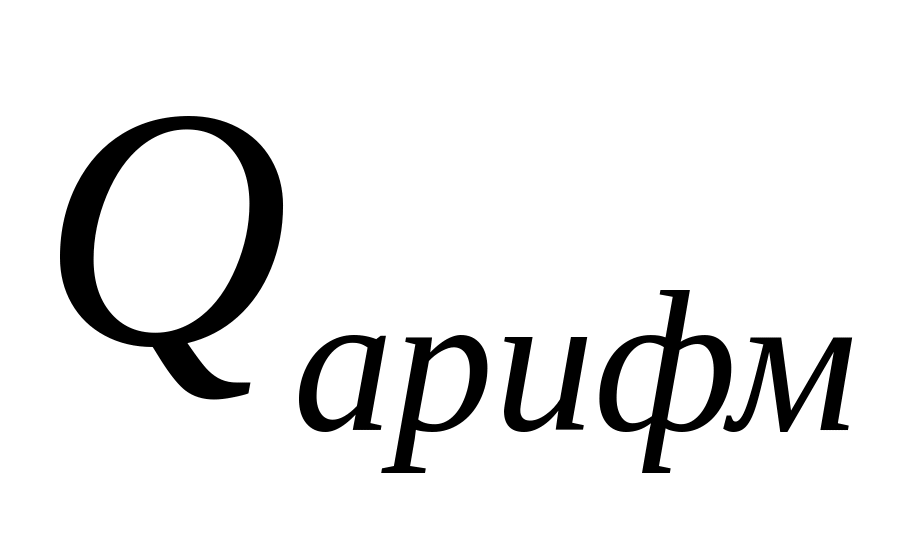 по заданной формуле свертывания (по
формуле среднего арифметического
взвешенного):
по заданной формуле свертывания (по
формуле среднего арифметического
взвешенного):
![]() ,
,
где
![]() - весовой коэффициент показателей
качества,
- весовой коэффициент показателей
качества,
![]() ;
;
![]() - количество
показателей (характеристик).
- количество
показателей (характеристик).
По результатам оценки объекты можно ранжировать по комплексным показателям качества в следующем порядке: слева располагается объект с наибольшим комплексным показателем, затем слева направо располагаются объекты по уменьшению значения комплексного показателя.
Рассчитать комплексный показатель качества исследуемого объекта
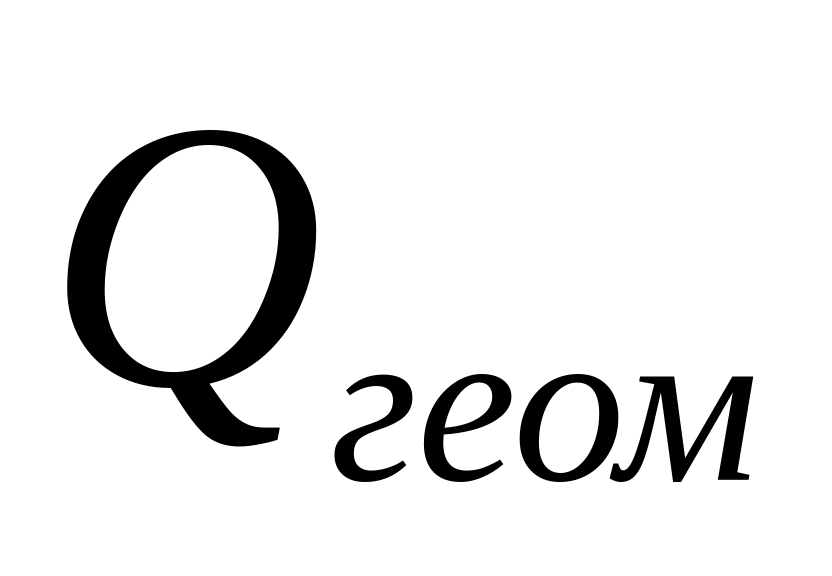 по заданной
формуле свертывания (по формуле среднего
геометрического взвешенного):
по заданной
формуле свертывания (по формуле среднего
геометрического взвешенного):
![]()
По результатам оценки объекты можно ранжировать по комплексным показателям качества в следующем порядке: слева располагается объект с наибольшим комплексным показателем, затем слева направо располагаются объекты по уменьшению значения комплексного показателя.
Рассчитать комплексный показатель качества исследуемого объекта
 по заданной
формуле свертывания (по формуле среднего
квадратического взвешенного):
по заданной
формуле свертывания (по формуле среднего
квадратического взвешенного):
![]()
По результатам оценки объекты можно ранжировать по комплексным показателям качества в следующем порядке: слева располагается объект с наибольшим комплексным показателем, затем слева направо располагаются объекты по уменьшению значения комплексного показателя.
Написать полученные цепочки ранжированных объектов (полученные цепочки ранжированных объектов могут различаться из-за округлений). Сравнить полученные результаты.
Сделать вывод.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ЗАДАЧИ 2 ПО ВАРИАНТАМ:
Необходимо выбрать наиболее эффективно работающее предприятие из шести предприятий. Показатели эффективности работы предприятий общие для всех вариантов. Исходные данные приведены в табл. 2.1.
Таблица 2.1. Исходные данные
Номер предприятия |
Показатели эффективности работы предприятий |
|||
Валовая прибыль, млн.руб. |
Эксплуатацион-ные расходы, млн.руб. |
Рентабель-ность активов, % |
Фондоотдача, руб./руб. |
|
I |
130,0 |
890,0 |
6,5 |
0,2 |
II |
125,0 |
750,0 |
7,8 |
0,3 |
III |
140,0 |
910,0 |
9,3 |
0,1 |
IV |
128,0 |
805,0 |
5,1 |
0,4 |
V |
115,0 |
796,0 |
7,4 |
0,3 |
VI |
150,0 |
865,0 |
8,2 |
0,2 |
Значения весовых коэффициентов определяются по варианту (последняя цифра шифра студента). Приведены в табл. 2.2.
Таблица 2.2. Исходные данные
Наименование показателей эффективности работы предприятия |
Значения весовых коэффициентов |
|||||||||
Варианты |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Валовая прибыль |
0,3 |
0,4 |
0,5 |
0,3 |
0,3 |
0,4 |
0,5 |
0,2 |
0,2 |
0,6 |
Эксплуатационные расходы |
0,2 |
0,1 |
0,2 |
0,3 |
0,4 |
0,2 |
0,1 |
0,5 |
0,4 |
0,1 |
Рентабельность активов |
0,3 |
0,3 |
0,2 |
0,2 |
0,2 |
0,1 |
0,3 |
0,1 |
0,2 |
0,1 |
Фондоотдача |
0,2 |
0,2 |
0,1 |
0,2 |
0,1 |
0,2 |
0,1 |
0,2 |
0,2 |
0,2 |
Задача для примера:
Для примера будет решена предыдущая задача.
Выбрать лучшую марку часов. Технические характеристики (по шкале порядка) ряда марок часов даны в табл. 2.3.
Таблица 2.3. Исходные данные
Прибор
|
Технические характеристики
|
||
Класс точности
|
Диапазон температур
|
Устойчивость к механическим
воздействиям* |
|
М1 |
1,5 |
–40…+60 |
0,75 (УП) |
М2 |
1,5 |
–30…+50 |
1,0 (ВУ) |
М3 |
1,0 |
–30…+60 |
0,75 (ВП) |
М4 |
1,0 |
–40…+60 |
1,0 (УУ) |
* УП – ударопрочные; ВУ – виброустойчивые; ВП – вибропрочные; УУ – удароустойчивые; i – номера приборов; j – номера единичных показателей качества |
|||
Значения весовых коэффициентов приведены в табл. 2.4.
Таблица 2.4. Исходные данные
Наименование технических характеристик часов |
Значения весовых коэффициентов |
Класс точности |
0,5 |
Диапазон температур |
0,2 |
Устойчивость к механическим воздействиям |
0,3 |
Решение.
Класс точности – положительный показатель,
диапазон температур – положительный показатель,
устойчивость к механическим воздействиям – положительный показатель;
Определяем базовые (эталонные) показатели по каждой технической характеристике в таблице 2.5.
Таблица 2.5. Расчетная таблица
Прибор
|
Технические характеристики |
||
Класс точности , % |
Диапазон температур , С |
Устойчивость к механическим воздействиям* , ед. |
|
М1 |
1,5 |
∆ = 100 |
0,75 |
М2 |
1,5 |
∆ = 80 |
1,0 |
М3 |
1,0 |
∆ = 90 |
0,75 |
М4 |
1,0 |
∆ = 100 |
1,0 |
Базовые
показатели
|
1,5 |
100 |
1,0 |
Определяем единичные показатели качества относительно базового (эталонного) показателя по каждой технической характеристики:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Результаты расчетов приведены в табл. 2.6.
Таблица 2.6. Единичные показатели качества
Прибор
|
Единичные относительные показатели качества |
||
аi1 |
аi2 |
аi3 |
|
М1 |
1,00 |
1,0 |
0,75 |
М2 |
1,00 |
0,8 |
1,00 |
М3 |
0,67 |
0,9 |
0,75 |
М4 |
0,67 |
1,0 |
1,00 |
Определяем комплексный показатель качества исследуемого объекта по формуле среднего арифметического взвешенного:
![]()
![]()
![]()
![]()
По результатам оценки приборы можно ранжировать по комплексным показателям качества в следующем порядке:
М2 > М1 > М4 > М3.
Определяем комплексный показатель качества исследуемого объекта по формуле среднего геометрического взвешенного:
![]()
![]()
![]()
![]()
По результатам оценки приборы можно ранжировать по комплексным показателям качества в следующем порядке:
М2 > М1 > М4 > М3.
Определяем комплексный показатель качества исследуемого объекта по формуле среднего квадратического взвешенного:
![]()
![]()
![]()
![]()
По результатам оценки приборы можно ранжировать по комплексным показателям качества в следующем порядке:
М2 > М1 > М4 > М3.
Результаты ранжирования по комплексным показателям качества приборов совпали. Независимо от того какой из вариантов расчета комплексного показателя качества (среднее арифметическое, среднее геометрическое и среднее квадратическое) был использован получен следующий результат:
М2 > М1 > М4 > М3.
Вывод: Лучший показатель качества у прибора (часов) М2.
