4.2 Пример расчета
Определить координаты центра тяжести составного сечения, приведенного на рисунке.
Рис. 18. Схема составного сечения
Решение:
1. Для решения
задачи используем методы разбиения на
части и отрицательных масс. Разбиваем
фигуру на пять простых элементов:
прямоугольник 1 размерами
;
полукруг 2 радиуса
;
треугольник 3 (вырез); полукруг 4 радиуса
(вырез); треугольник 5. Вводим систему
координат
с началом в точке О.
2. Определяем
площади
и координаты
центров тяжести
составных элементов.
Прямоугольник 1:
Треугольник 3:
|
Полукруг 2:
Полукруг 4:
|
Треугольник 5:
|
|
3. Находим статические моменты сечения относительно осей x,y:
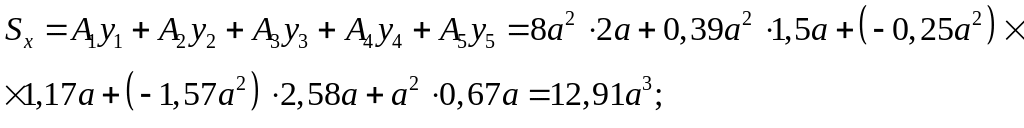
Площадь сечения:
.
4. Находим координаты центра тяжести:
Наносим центр тяжести на чертеж (рис. 19).
Рис. 19
5 УсловиЯ заданиЙ к расчетно-графической работе
Задача 1. Определение реакций опор твердого тела
На схемах показаны три способа закрепления бруса, ось которого - ломаная линия. Задаваемая нагрузка и размеры во всех трех случаях одинаковы. Составить уравнения равновесия для определения реакций опор для всех трех случаев закрепления. Для одной из схем (по указанию преподавателя) провести расчет реакций связей с проверкой полученных результатов. Схемы бруса приведены на рис. 20, числовые данные – в таблице 2.
Таблица 2. Числовые данные к задаче 1
№ варианта |
F, кН |
q, кН/м |
M, кН∙м |
a, м |
b, м |
α, град |
β, град |
1 |
20 |
2 |
11 |
1,2 |
1,3 |
26 |
15 |
2 |
25 |
6 |
14 |
1,6 |
2,3 |
31 |
31 |
3 |
10 |
9 |
12 |
2,1 |
1,7 |
43 |
44 |
4 |
12 |
3 |
9 |
1,9 |
1,8 |
37 |
62 |
5 |
6 |
5 |
18 |
2,5 |
2,1 |
24 |
71 |
6 |
18 |
4 |
15 |
1,4 |
2,5 |
21 |
23 |
7 |
14 |
11 |
12 |
1,1 |
1,0 |
15 |
54 |
8 |
8 |
6 |
10 |
1,5 |
1,7 |
19 |
18 |
9 |
11 |
8 |
8 |
2,5 |
2,0 |
47 |
35 |
10 |
15 |
7 |
16 |
1,7 |
1,1 |
67 |
39 |
11 |
23 |
10 |
18 |
1,6 |
1,5 |
49 |
27 |
12 |
17 |
6 |
15 |
1,8 |
1,3 |
51 |
45 |
13 |
11 |
5 |
14 |
2,3 |
1,3 |
35 |
32 |
14 |
15 |
9 |
18 |
1,7 |
1,8 |
39 |
40 |
15 |
18 |
8 |
21 |
1,1 |
2,1 |
55 |
21 |
16 |
12 |
11 |
9 |
2,6 |
1,9 |
61 |
46 |
17 |
7 |
7 |
13 |
1,4 |
1,6 |
78 |
38 |
18 |
11 |
4 |
16 |
1,7 |
1,5 |
54 |
61 |
19 |
9 |
10 |
15 |
1,9 |
1,8 |
32 |
45 |
20 |
11 |
5 |
19 |
2,0 |
2,3 |
14 |
47 |
21 |
23 |
6 |
10 |
2,3 |
1,4 |
21 |
34 |
22 |
5 |
11 |
9 |
1,6 |
1,8 |
66 |
23 |
23 |
9 |
8 |
14 |
1,8 |
1,9 |
22 |
54 |
24 |
16 |
9 |
18 |
1,5 |
2,2 |
19 |
39 |
25 |
13 |
12 |
11 |
1,9 |
2,4 |
34 |
44 |
26 |
14 |
6 |
16 |
1,0 |
2,5 |
50 |
35 |
27 |
22 |
3 |
17 |
2,3 |
1,7 |
46 |
42 |
28 |
17 |
9 |
12 |
2,2 |
1,5 |
59 |
19 |
29 |
14 |
7 |
13 |
1,9 |
2,1 |
76 |
37 |
30 |
18 |
8 |
10 |
1,3 |
1,8 |
63 |
51 |
Рис. 20. Схемы к задаче 1
Продолжение рис. 20
Продолжение рис. 20
Продолжение рис. 20
