Интегрирование тригонометрических функций.
Задача 5. Вычислить интеграл
.
Решение. Функция не обладает
свойствами чётности или нечётности, то
есть, сменив знак синуса или косинуса,
мы не получим, что знак минус будет у
всей дроби. Поэтому применяем универсальную
тригонометрическую подстановку:
.
Напомним, что при этом
,
,
,
.
Итак, сделаем замену:
=
=
=
=
=
.
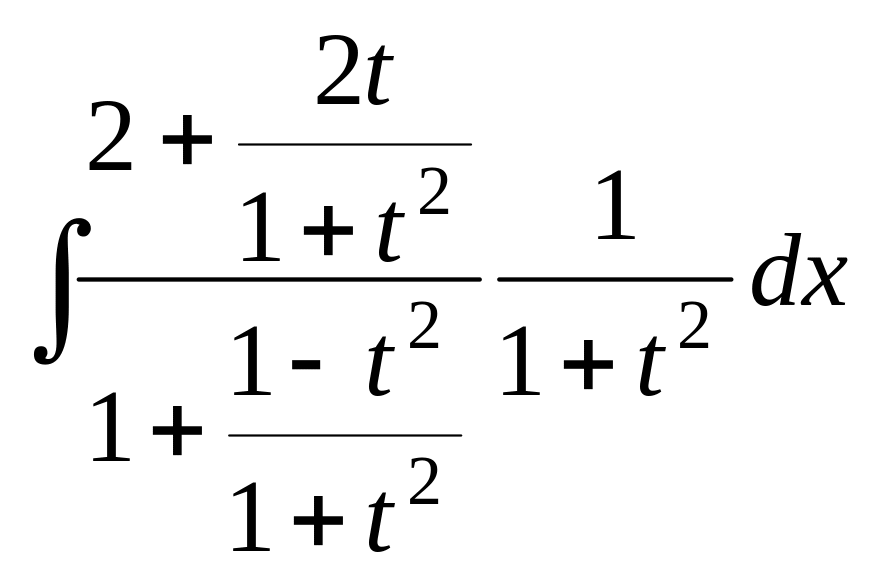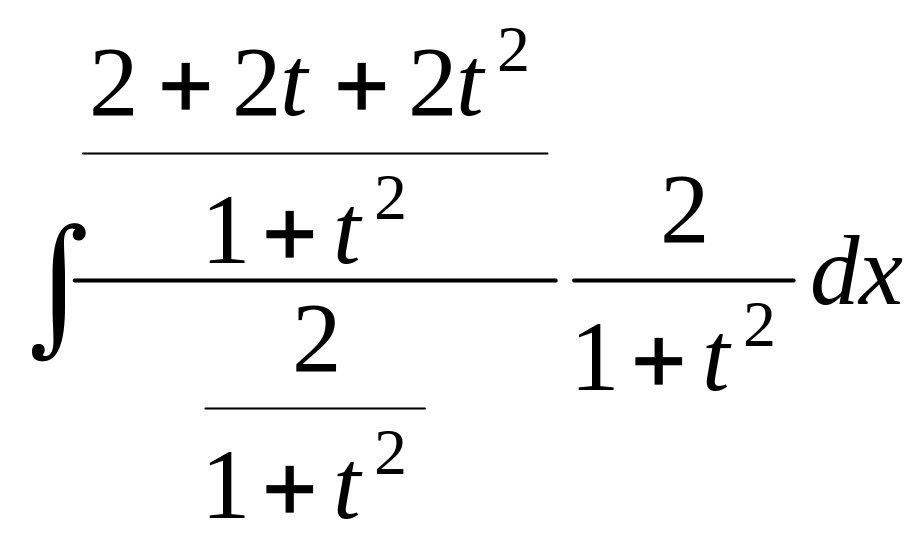Теперь сделаем обратную замену.
Ответ.
=
.
Задача 6. Вычислить интеграл
.
Решение. Сделаем замену .
=
=
вот и свелось к рациональной дроби, и
дальше для t можем
действовать в рамках прошлой темы
«рациональные дроби».
=
=
=
.
Приводим к общему знаменателю:
=
,
далее
,
,
отсюда следует
.
=
=
это можно после обратной замены и
применения свойств логарифмов, записать
так:
.
Ответ. .
Задача 7. Вычислить интеграл
.
Решение. Здесь, как и в прошлом примере, функция нечётная относительно косинуса, замена ,
,
,
.
Однако в этом примере квадратные корни
не сокращаются, а наоборот, умножаются,
ведь косинус теперь не в числителе, а в
знаменателе:
.
Но всё равно, будет чётная степень корня:
.
Итак,
,
что равно
=
.
Теперь мы можем воспользоваться тем разложением, которое получали для такого случая в теме «рациональные дроби» на прошлой практике, см. задачу, где оба корня знаменателя кратные.
Курс специально построен так, чтобы использовать некоторые коэффициенты из старых примеров и не искать их здесь повторно.
Разложение было такое:
.
После приведения к общему знаменателю и решения системы уравнений, там получалось , , , .
Итак,
=
=
=
=
=
.
Сделаем обратную замену.
.
Ответ.
.
Задача 8. Вычислить интеграл
.
Решение. Здесь нечётная степень
синуса, применяем замену
.
Тогда
=
=
=
=
=
=
.
Ответ. .
Задача 9. Вычислить интеграл
.
Решение. Здесь суммарная степень
чётная, то есть, если сменить знак перед
sin и cos, то
знак сменится 2 раза, и останется «+».
Поэтому надо применить замену
.
Тогда (см. в лекции):
.
,
.
=
=
=
=
=
=
.
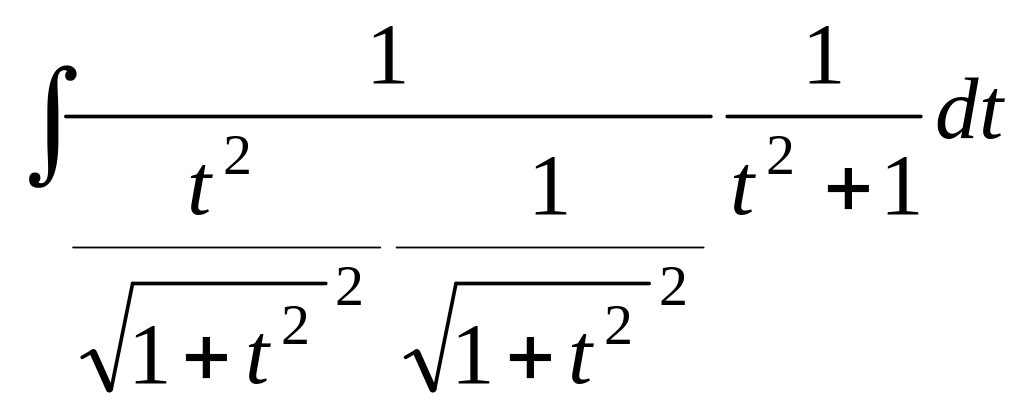После обратной замены получается:
.
Ответ. .
Задача 10. Вычислить интеграл
.
Решение. Здесь тоже суммарная степень чётная, замена .
. , .
=
=
=
=
=
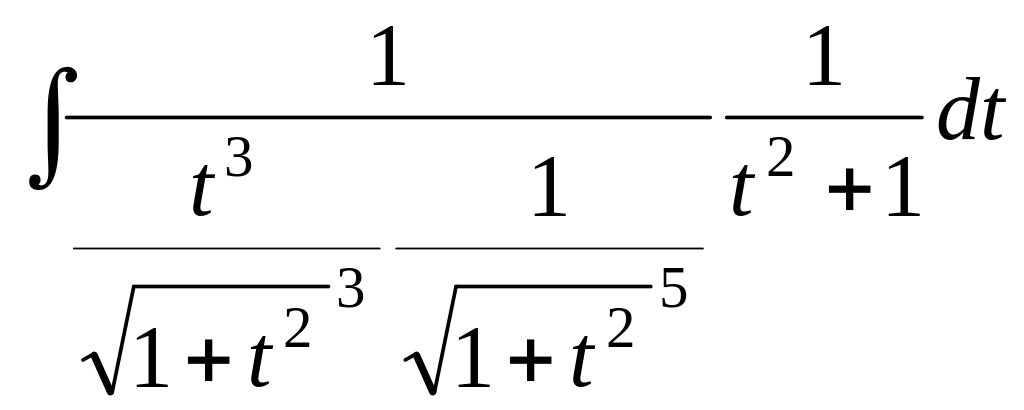здесь мы воспользовались формулой
.
=
.
После обратной замены получаем ответ:
Ответ.
.
ПРАКТИКА № 6.
Иррациональности, содержащие сумму или разность квадратов.
Задача 1. Вычислить интеграл
.
Решение. В этом случае нужно замена
(см. лекции)
.
Приэтом корень квадратный исчезает:
=
=
=
.
=
=
.
Итак,
=
=
=
.
Для обратной замены, вспомним, что
,
то есть
,
.
Тогда
=
.
Получается, что надо найти котангенс
того угла, синус которого равен
.
Подпишем соответствующие стороны на
чертеже прямоугольного треугольника.
Третья сторона вычисляется по теореме Пифагора: .
Тогда котангенс этого угла:
.
=
=
.
Задача 2. Вычислить интеграл
.
Решение. Здесь под корнем сумма
квадратов, и при этом
,
поэтому замена
.
Тогда
,
=
=
=
=
=
=
=
=
=
.
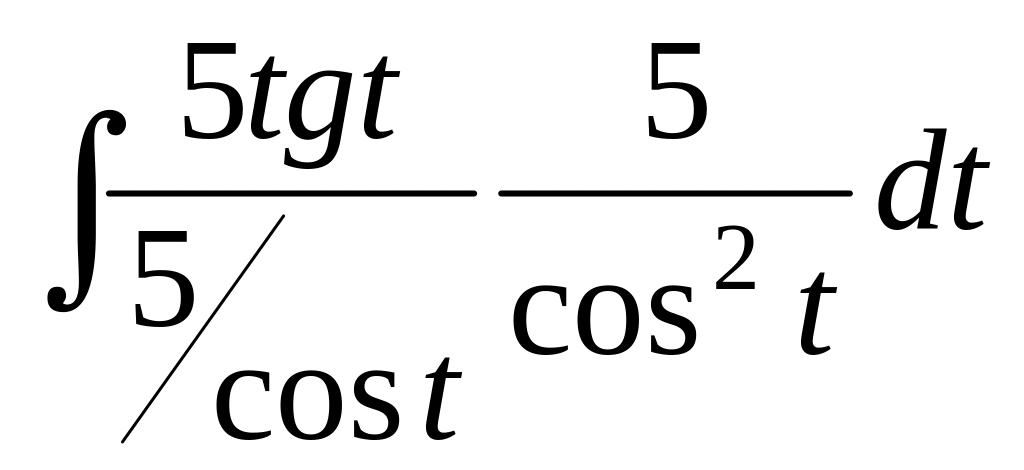Сделаем обратную замену.
,
то есть
.
Тогда
=
.
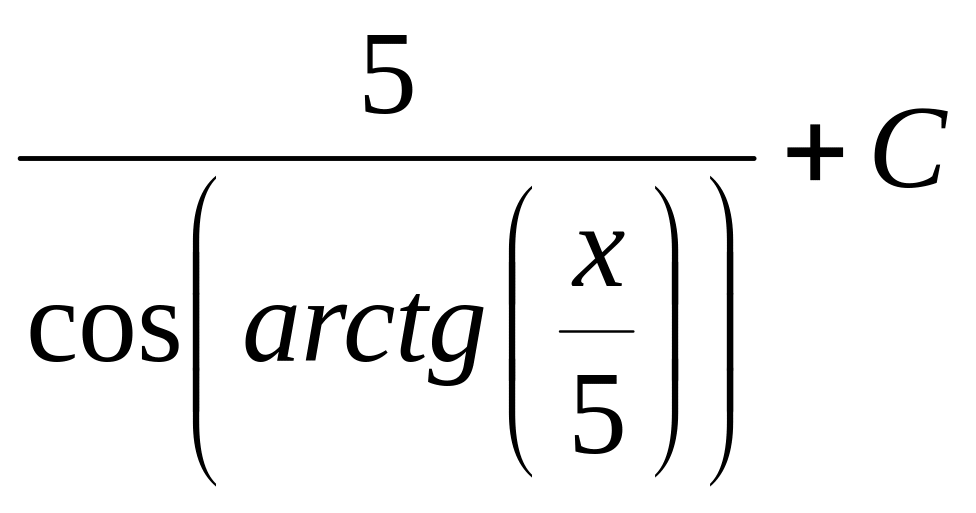Упростим композицию (косинус арктангенса)
с помощью прямоугольного треугольника,
как в прошлой задаче. Тангенс некоторого
угла равен
,
а требуется найти его косинус.
Подпишем 2 катета x и 5.
Гипотенуза легко вычислится по теореме
Пифагора. Теперь видно, что косинус это
.
Итак,
=
.
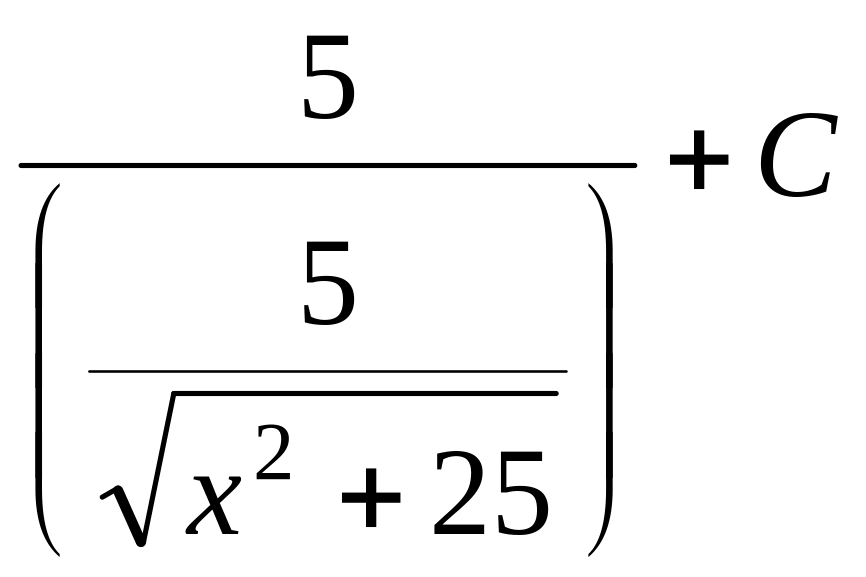Ответ: .