7.5. Интегральная теорема Муавра-Лапласа

Следствиями центральной предельной теоремы являются рассмотренные ранее локальная и интегральная теоремы Муавра-Лапласа. Приведем вывод интегральной теоремы Муавра-Лапласа.

Рассмотрим схему Бернулли. Пусть - число появления события А (число успехов) в n независимых испытаниях, в каждом из которых оно может появиться с вероятностью р (не появиться с вероятностью ). Случайную величину можно представить в виде суммы n независимых случайных величин таких, что , если в i-м испытании событие А наступило, и , в противном случае, т.е.

.

Так как , , то

, .

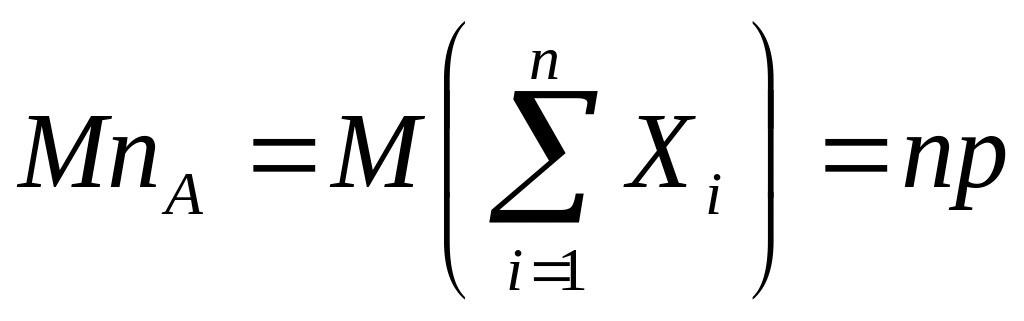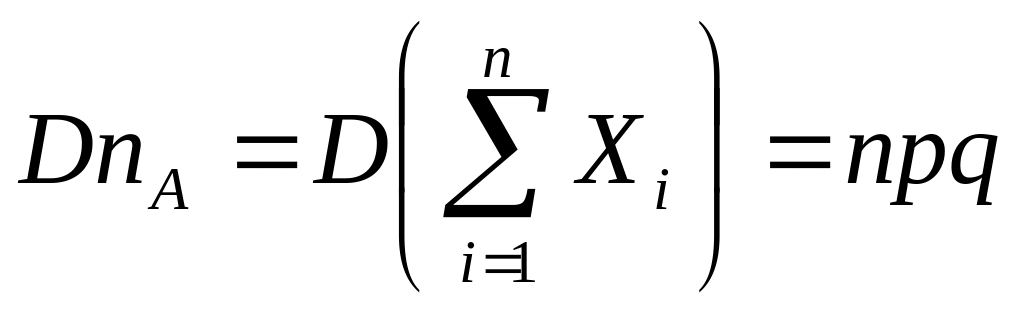Тогда случайная величина

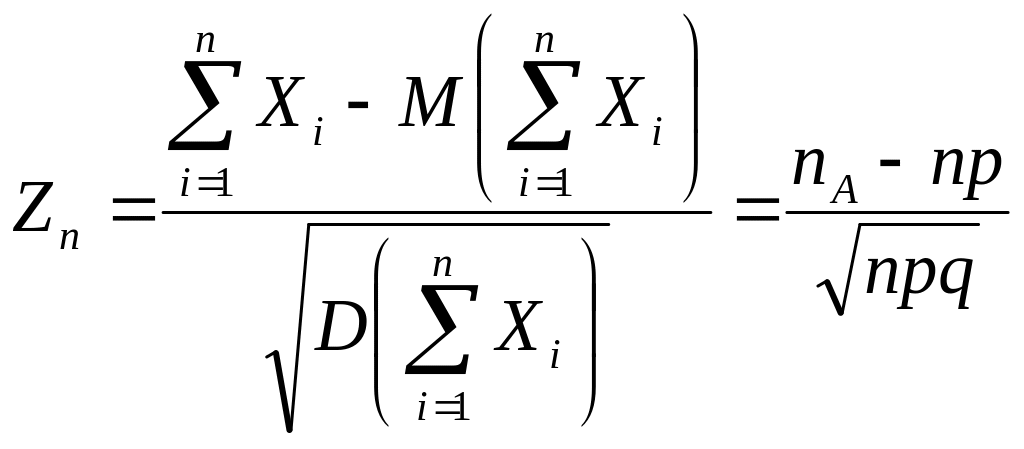
представляет также сумму n независимых, одинаково распределенных случайных величин. При этом , действительно:

,

Следовательно, на основании центральной предельной теоремы (7.13) случайная величина Z_n при большом числе n имеет приближенно нормальное распределение. По свойству нормального закона, записываем

,

- функция Лапласа.

Полагая

, ,

двойное неравенство

можно переписать в эквивалентном виде . Таким образом, получаем

,

т.е. интегральную теорему Муавра-Лапласа.

Заметим, что интегральная предельная теорема Муавра-Лапласа

(7.15)

для схемы Бернулли непосредственно вытекает из центральной предельной теоремы с учетом того, что , , . Тогда , .

Для подсчета сумм биноминальных вероятностей можно воспользоваться приближенной формулой

,

(7.16)

где - функция Лапласа.

Пример 7.4. Машинистке требуется напечатать текст, содержащий 8000 слов, состоящих из четырех и более букв. Вероятность сделать ошибку в любом из этих слов равна 0,01. Какова вероятность, что при печатании будет сделано не более 90 ошибок?

Решение:

Применим формулу (5.16). Так как , , , , то

,

, .

Следовательно, .