1. Определение опорного плана транспортной задачи методом северо-западного угла.

Замечание.

Сущность каждого из методов нахождения опорного плана состоит в том, что опорный план находится за

(n + m - 1) шагов.

На каждом шаге в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворения потребностей в грузе одного из пунктов назначения, либо вывоз груза из одного из пунктов отправления.

В методе северо-западного угла заполнение начинается с верхней левой(северо-западной) клетки.

Рассмотрим метод северо-западного угла на примере.

Пример.

Имеется 4 пункта назначения и 3 пункта отправления.

Запасы грузов соответственно равны:

потребности:

Матрица C(тарифы) имеет следующий вид:

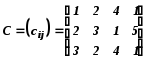
Пункты отправления	Пункты назначения				Запасы
					50
					30
					10
Потребности	30	30	10	20

Получили начальный опорный план методом северо-западного угла.

При определении оптимального плана будем использовать метод потенциала.

2. Метод потенциала.

Теорема 2.

(для транспортной задачи)

Если для некоторого опорного плана транспортной задачи существуют такие числа , для которых соблюдается:

то этот опорный план называется оптимальным планом транспортной задачи.

Числа называются потенциалами:

- потенциалы пунктов назначения;

- потенциалы пунктов отправления.

Базируясь на этой теореме можно построить алгоритм нахождения решения транспортной задачи.

Суть метода:

1. для каждой из заполненных клеток составляют уравнения 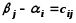. Таких уравнений должно быть (n + m - 1). Имеется система из (n + m - 1) уравнений, а неизвестных будет (n + m). Поэтому можно положить какое-то неизвестное, например, 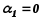и найти решение системы уравнений.

Иногда, в литературе встречается запись , но эта запись ничего не меняет;

2. после определения всех потенциалов 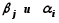для каждой свободной клетки определяется число

;

3. если среди чисел 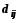нет положительных, то опорный план, в соответствии с теоремой 2, является оптимальным;

4. если существует хотя бы одна свободная клетка, в которой 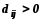, то исходный план не является оптимальным;

5. рассматриваются все свободные клетки, для которых 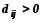и среди них выбирают ту клетку, для которой 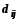- максимально. Эту клетку фиксируют и осуществляется переход к следующему опорному плану.

Замечание.

Мы будем использовать понятие цикла.

Циклом в таблице условий транспортной задачи будем называть ломаную линию, вершины которой, кроме одной, расположены в занятых клетках.

Ребра располагаются вдоль строк и вдоль столбцов.

В каждой вершине цикла встречаются ровно два звена: одно из которых находится в строке, а другое - в столбце.

Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами:

отмеченная точка не является вершиной.

При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки построен цикл, осуществляется переход к новому опорному плану транспортной задачи.

Переход к новому опорному плану осуществляется путем перемещения грузов в пределах клеток, связанных циклом с данной свободной клеткой.

Перемещение грузов осуществляется по следующим правилам:

1. каждой из клеток, связанной циклом с данной свободной клеткой (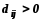) приписывают определенный знак(свободной клетки приписывают знак «+», а всем остальным клеткам поочередно знаки «+» и «-»).

2. в данную свободную клетку переносят меньшее из чисел 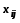(наименьший груз, стоящий в минусовых клетках). Одновременно это 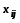прибавляют к соответствующим 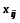( 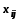- стоящие в плюсовых клетках) и отнимают от соответствующих 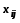( 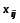- стоящие в минусовых клетках).

В результате описанных преобразований(преобразований по пунктам (1) и (2)) свободная клетка становится занятой, а ранее занятая клетка - клетка, в которой стояло наименьшее значение в вершинах цикла(на значит, что наименьшее из всех), становится свободной. Таким образом занятых клеток (n + m - 1).

Замечание.

Если в клетках со знаком «-» стоят значения одинаковые по величине и они являются минимальными, то освобождают только одну клетку, а в остальных клетках ставят ноль.

Таким образом осуществляется переход от одного опорного плана к другому. Такой переход называют сдвигом по циклу пересчета.

Полученный опорный план транспортной задачи проверяется на оптимальность(в соответствии с теоремой). Если план не оптимален, то осуществляем переход к следующему опорному плану и так далее, до перехода к оптимальному плану транспортной задачи.

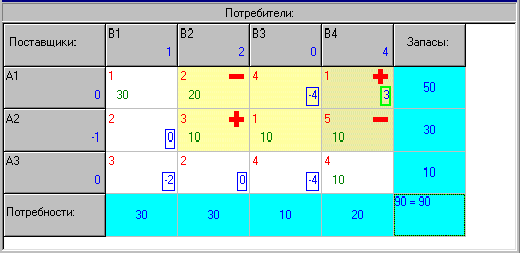
Пример.

Вернемся к рассмотренному ранее примеру.

Строим систему уравнений в соответствии с теоремой:

уравнений шесть, а неизвестных - семь.

полагаем:

1. Выбираем свободную клетку с наибольшим положительным ;

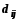2. Строим цикл(одна пустая клетка - другие заполненные);

3. Делаем цикл пересчета: среди минусовых клеток находим минимальное - 10. Ставим плюсы и минусы в узлах цикла. Начинаем переброс(к плюсовым клеткам прибавляем 10, от минусовых отнимаем 10) и получаем новый опорный план.

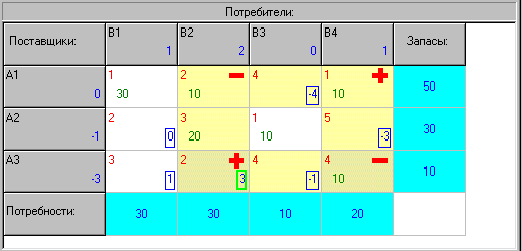
План является допустимым, проверим его на оптимальность.

Строим систему уравнений в соответствии с теоремой:

полагаем:

Выбираем свободную клетку с наибольшим положительным , , план не является оптимальным и мы осуществляем цикл пересчета и получаем новый опорный план.

План является допустимым, проверим его на оптимальность.

Строим систему уравнений в соответствии с теоремой:

полагаем:

Проанализируем: является ли этот план оптимальным.

Все - это говорит о том, что план является оптимальным.

Найдем теперь целевую функцию:

- минимальное значение.

Получили оптимальный план перевозок.