
Табличное представление симплекс - метода.
Пусть имеется начальный базис B, соответствующий начальной экстремальной точке. Целевая функция и ограничения задачи линейного программирования могут быть записаны в виде:
строка - целевая функция
![]()
строки-ограничения
![]()
Эти равенства можно свести в следующую симплекс - таблицу, в которой правая часть(ПЧ) соответствует их правым частям.
|
|
|
|
ПЧ |
|
1 |
|
|
0 |
|
0 |
B |
N |
b |
Строки-ограничения
преобразуются умножением на (![]() ).
К строке целевая
функция прибавляются
новые строки- ограничения, умноженные
на
).
К строке целевая
функция прибавляются
новые строки- ограничения, умноженные
на
![]() .
При этом получается следующая
преобразованная таблица:
.
При этом получается следующая
преобразованная таблица:
|
|
|
|
|
ПЧ |
|
|
1 |
|
|
|
|
|
0 |
1 |
|
|
Базисные переменные отмечены в таблице слева, а значения базисных переменных записаны в правой части таблицы.
Эта таблица содержит всю информацию, необходимую для завершения первого шага симплекс метода.
Если
![]() процесс прекращается, то есть текущая
точка является оптимальной.
процесс прекращается, то есть текущая
точка является оптимальной.
В противном случае:
при просмотре строки целевой функции можно выбрать внебазисную переменную с положительным значением
![]()
где
![]() -
вектор
-
вектор
![]() - матрица
- матрица
![]() -
вектор
-
вектор
![]() - скаляр
- скаляр
Если
![]() - то процесс прекращается - значениецелевой функции
неограниченно.
- то процесс прекращается - значениецелевой функции
неограниченно.
Если
![]() ,
то
,
то
так как
![]() записаны
подПЧ и
записаны
подПЧ и
![]() соответственно,
то следуя ( 6.4 .0 ) легко вычислить
соответственно,
то следуя ( 6.4 .0 ) легко вычислить![]() .
.
Базисная переменная
![]() ,
соответствующая минимальному отношению
в ( 6.4 .0 ), выводится из базиса, а
,
соответствующая минимальному отношению
в ( 6.4 .0 ), выводится из базиса, а![]() вводится
в базис.
вводится
в базис.
Далее проводим ведущее преобразование:
Строка, соответствующая
![]() (выводимая
переменная из базиса) - ведущая строка.
(выводимая
переменная из базиса) - ведущая строка.
Столбец, соответствующий
![]() (вводимая
переменная в базис) - ведущий столбец.
(вводимая
переменная в базис) - ведущий столбец.
Разделить ведущую строку(соответствующую
 )
на ведущий элемент
)
на ведущий элемент ;
;Умножить новую r - ую строку на
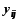 и результат вычесть изi
- ой строки
ограничений для всех
и результат вычесть изi
- ой строки
ограничений для всех
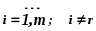
Умножить новую r - ую строку на
 и результат вычесть из строки целевой
функции.
и результат вычесть из строки целевой
функции.
Пример:
![]()
![]()
![]()
![]()
Графически:
A(4/3,
11/3)
(0,3)
(0,0) (5,0)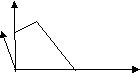

Оптимальной является
точка
![]() . Значение функции
. Значение функции![]()
приводим задачу линейного программирования к канонической форме:
![]()
![]()
![]()
![]()
![]()
![]()
Возьмем в качестве В матрицу
![]()
Так как
![]() ,
,
то найдена экстремальная точка:
|
|
|
|
|
|
|
ПЧ |
|
|
1 |
-1 |
3 |
0 |
0 |
0 |
|
|
0 |
-1 |
2 |
1 |
0 |
6 |
|
|
0 |
1 |
1 |
0 |
1 |
5 |
![]() - выводится из базиса
- выводится из базиса
![]() - вводится в базис
- вводится в базис
Новый базис
![]()
|
|
|
|
|
|
|
ПЧ |
|
|
1 |
|
0 |
|
0 |
-9 |
|
|
0 |
|
1 |
|
0 |
3 |
|
|
0 |
|
0 |
|
1 |
2 |
Теперь:
![]() -
выводится из базиса
-
выводится из базиса
![]() -
вводится в базис.
-
вводится в базис.
Новый базис
![]()
|
|
|
|
|
|
|
ПЧ |
|
|
1 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
0 |
1 |
0 |
|
|
|
Так как
![]() , то полученооптимальное
решение.
, то полученооптимальное
решение.
Выбор начальной экстремальной точки.
Для использования симплекс - метода необходимо задать некоторую начальную экстремальную точку.
Из теоремы(о характеристиках
экстремальных точек) нахождение начальной
экстремальной точки связано с разбиением
матрицы A
на
![]() ,
,
где В - матрица m x m полного ранга, называемая базисом.
N - матрица m x (n-m) ,
так чтобы
![]() .
В предыдущем примере начальная точка
определялась легко. В практических
задачах определить начальную точку не
так - то легко. Для этого используются
различные приемы.
.
В предыдущем примере начальная точка
определялась легко. В практических
задачах определить начальную точку не
так - то легко. Для этого используются
различные приемы.
Начальная точка может быть получена введением искусственных переменных.
Рассмотрим два метода
выбора начальной экстремальной точки.
Для обоих методов предварительно
необходимо привести задачу к каноническому
виду
![]()
![]() (причем предполагается, что
(причем предполагается, что![]() (если
(если![]() ,
то i
- ое ограничение умножается на (-1))).
,
то i
- ое ограничение умножается на (-1))).
Двухэтапный метод:
на первом этапе решения задачи вводится вектор
 -
вектор искусственных переменных
размерностиm.
-
вектор искусственных переменных
размерностиm.
![]()
![]()
![]()
где
![]() - вектор, все компоненты которого равны
единице.
- вектор, все компоненты которого равны
единице.
После окончания первого этапа:
либо
![]() ,
либо
,
либо![]()
Если
![]() исходная система несовместна, то есть
допустимая область пуста.
исходная система несовместна, то есть
допустимая область пуста.
Если
![]() искусственные переменные выводятся
из базиса и таким образом получается
экстремальная точка исходной системы.
искусственные переменные выводятся
из базиса и таким образом получается
экстремальная точка исходной системы.
на втором этапе начиная из полученной точки решается задача минимизации целевой функции.
M - метод:
В этом методе также вводятся искусственные переменные и каждой искусственной переменной назначается большой положительный штраф M (больше любого ci )
Задача линейного программирования принимает вид:
![]()
![]()
![]()
Если в оптимальном
решении
![]() ,
то это означает, что получено решение
исходной задачи.
,
то это означает, что получено решение
исходной задачи.
Если
![]() ,
то это означает, что система (
,
то это означает, что система (![]()
![]() )
не имеет решения.
)
не имеет решения.
Замечание 1.
(зацикливание)
Одним из основных недостатков симплекс-метода является зацикливание, возникающее в тех случаях, когда на очередном шаге поиска приходится иметь дело с вырожденным базисным решением. Подобная ситуация характеризуется невозможностью перехода к новому допустимому базисному решению, она начинает повторяться с определенной частотой, зависящей от числа нулевых базисных переменных, и такое повторение может продолжаться довольно долго.
В принципе зацикливание преодолимо(оно встречается сравнительно редко) и в качестве практических рекомендаций может быть предложено несколько вариантов выбора следующей точки:
отказ от точки
 для которой
для которой ;
;случайный выбор новой угловой точки
и так далее.


