4. Влияние гидростатического давления, наложенного на одноосное растяжение, на интенсивность разрушающих напряжений и деформаций
Для титанового сплава ВТ2-0 построим зависимость интенсивности разрушающего напряжения и соответствующей разрушающей деформации от величины гидростатического давления p при одноосном растяжении в камере высокого давления. Зависимость строим по точкам, соответствующим значениям давления, приведенным в таблице 6. При построении зависимости будем использовать критерий разрушения Мора и деформационный критерий.
Изобразим напряженное состояние, возникающее при одноосном растяжении в камере высокого давления (рисунок 8).
|
Рисунок 8. Напряженное состояние при наложении гидростатического
давления p на одноосное растяжение
4.1. Критерий о. Мора
При
напряженном состоянии, изображенном
на рисунке 7,
и
;
выражение для интенсивности напряжений
принимает вид
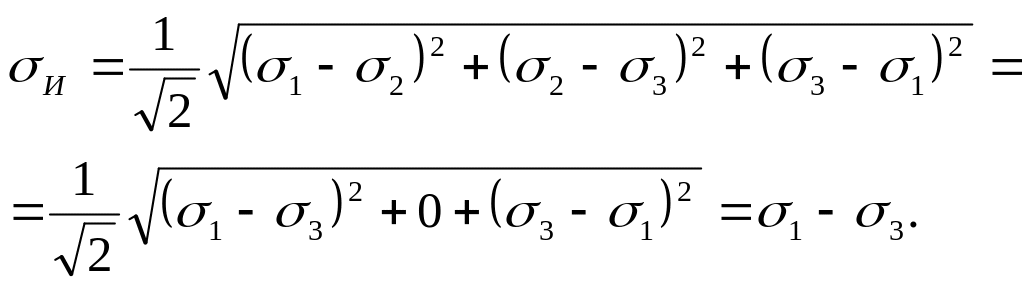(27)
Выразим из (27)
через
и
:
.
Результат подставим в формулу (15)
. (28)
Подставляя
значение
=0,433,
найденное в подразделе 3.1, преобразовываем
(28) дальше с учетом того, что
,
. (29)
Таким образом, для образца из титанового сплава ВТ2-0 по критерию Мора получена зависимость интенсивности напряжений в момент разрушения от величины гидростатического давления p при одноосном растяжении в камере высокого давления. Интенсивность разрушающей деформации найдем, применив степенную аппроксимацию кривой деформирования в виде (12), тогда
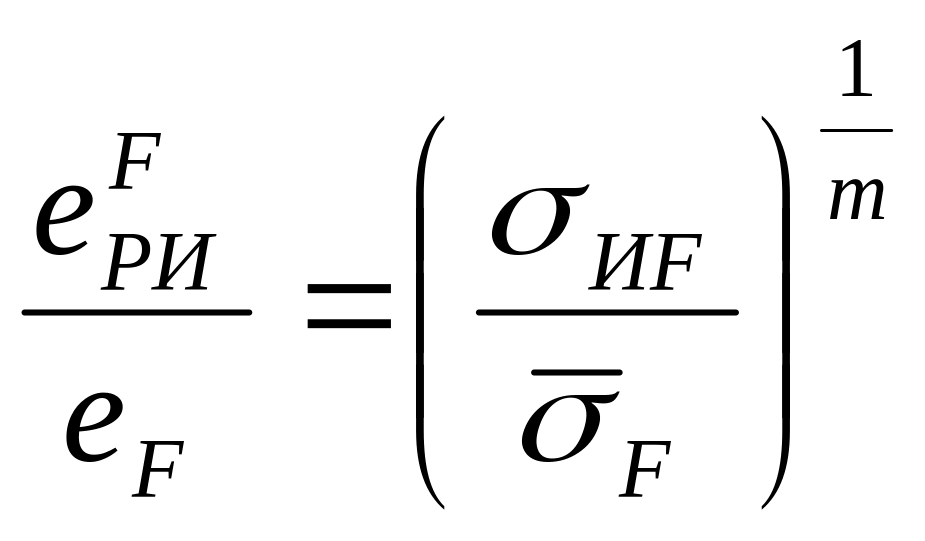, (30)
где m=0,067 – показатель упрочнения, был определен в разделе 2.
Результаты расчета представлены в таблице 13 и на рисунках 9 и 10.
Таблица 13. Зависимость разрушающей интенсивности напряжений и деформаций от величины гидростатического давления p по критерию Мора при одноосном растяжении в камере высокого давления для титанового сплава ВТ2-0.
|
0,000 |
0,200 |
0,400 |
0,600 |
0,800 |
1,000 |
|
1,000 |
1,113 |
1,227 |
1,341 |
1,454 |
1,567 |
|
1,000 |
4,971 |
21,146 |
79,148 |
266,121 |
816,854 |
4.2. Деформационный критерий
Условие разрушения по деформационному критерию (26) имеет вид
, (31)
где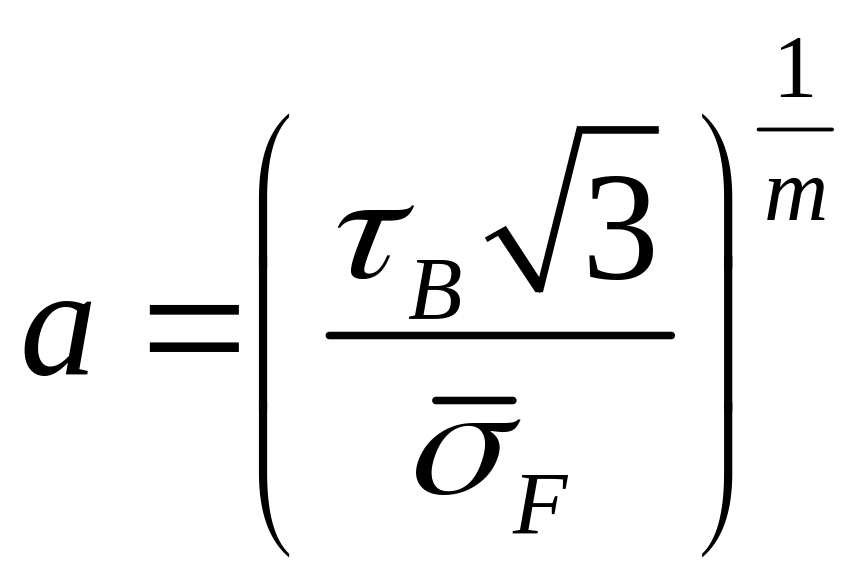 
,
, 
.
Характеристики титанового сплава ВТ2-0 приведены в таблице 1
МПа, 
.
Значения параметров a и b деформационной модели разрушения (31)
, 
.
Для
напряженного состояния (рисунок 8) найдем
параметры
и
.
Из (27)
находим
;
.
Подставим значения параметров a, b, m и выражения для и в деформационную модель (31)
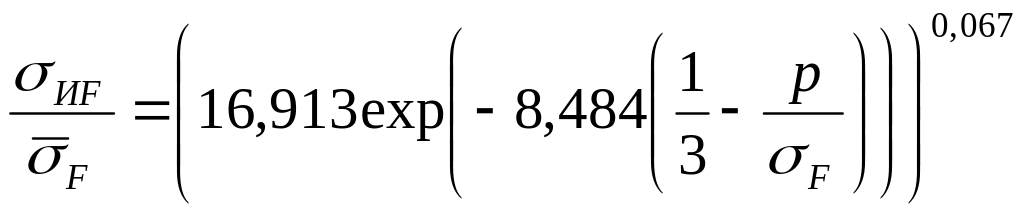. (32)
Выведем
зависимость между осевой разрушающей
нагрузкой
при действии гидростатического давления
p и истинным
сопротивлением разрыву
.
Подставим
в (27) выражения для
и
:
Полученное выражение для интенсивности разрушающего напряжения подставим в (28) и после элементарных преобразований получим
.
(33)
Теперь
заменим отношение
на
в (32), используя выражение (33), тогда
.
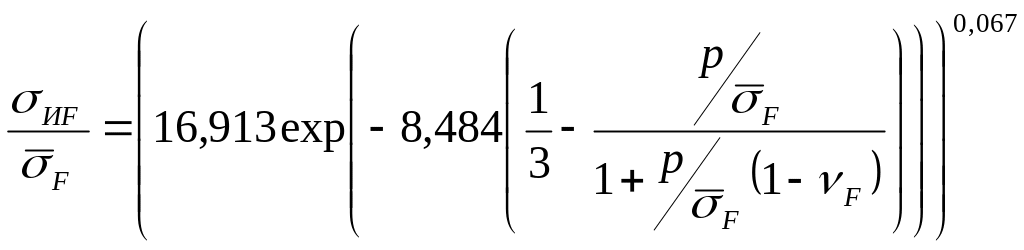(34)
Интенсивность разрушающей деформации найдем из соотношения (30).
Результаты расчета представлены в таблице 14 и на рисунках 9 и 10.
Таблица 14. Зависимость разрушающей интенсивности напряжений и деформаций от величины гидростатического давления p по деформационному критерию при одноосном растяжении в камере высокого давления для титанового сплава ВТ2-0.
|
0,000 |
0,200 |
0,400 |
0,600 |
0,800 |
1,000 |
|
1,000 |
1,107 |
1,204 |
1,291 |
1,367 |
1,437 |
|
1,000 |
4,591 |
15,903 |
44,646 |
106,696 |
224,784 |
1 - расчет по деформационному критерию;
2 - расчет по критерию О. Мора.
Рисунок 9. Зависимость интенсивности разрушающих напряжений от величины гидростатического давления p при одноосном растяжении в камере
высокого давления для титанового сплава ВТ2-0
1 - расчет по деформационному критерию;
2 - расчет по критерию О. Мора.
Рисунок 10. Зависимость интенсивности разрушающей деформаций от величины гидростатического давления p при одноосном растяжении в камере
высокого давления для титанового сплава ВТ2-0
Как следует из рисунков 9 и 10, наложение всестороннего гидростатического давления на одноосное растяжение повышает сопротивление материала разрушению в 1,437 раза по деформационному критерию и в 1,567 раза по критерию Мора, а так же повышает пластичность материала. Также можно отметить, что максимальная интенсивность разрушающей деформации, определенная по критерию Мора в 3,6 раза больше максимальной интенсивности разрушающей деформации по деформационному критерию. Деформационный критерий в отличии от критерия Мора, учитывает влияние всех главных напряжений, и по этому дает более точный результат.
ЗАКЛЮЧЕНИЕ
В данной работе выполнена аппроксимация кривой деформирования титанового сплава ВТ2-0 степенной функцией
.
По заданным механическим характеристикам для титанового сплава ВТ2-0 определены:
ресурс пластичности (пластическая деформация в момент разрушения)
;
истинное сопротивление разрыву
МПа.
Для пластичного материала титанового сплава ВТ2-0 в относительных координатах "интенсивность напряжений – интенсивность деформаций" построена обобщенная кривая деформирования. На кривой деформирования отмечены точки, соответствующие разрушающим значениям напряжений и деформаций при растяжении, сжатии, чистом сдвиге, плоском равноосном растяжении, плоском равноосном сжатии, неравноосном объемном растяжении.
С уменьшением "жесткости" напряженного состояния возрастает интенсивность соответствующей логарифмической деформации в момент разрушения и, следовательно, тем более вероятность вязкого разрушения. В точке 5 на обобщенной кривой деформирования, соответствующей равноосному плоскому сжатию (соответствующее напряженное состояние является самым "мягким" из отмеченных на кривой деформирования), моменту разрушения соответствует интенсивность логарифмической пластической деформации в 4838 раз больше ресурса пластичности материала при линейном напряженном состоянии. Интенсивность напряжений при этом в 1,765 раза выше истинного сопротивления разрыву.
В точке 6 на обобщенной кривой деформирования, соответствующей объемному растяжению (соответствующее напряженное состояние является самым "жестким" из отмеченных на кривой деформирования), моменту разрушения соответствует интенсивность логарифмической пластической деформации, составляющей 0,0003% ресурса пластичности материала при линейном напряженном состоянии. Интенсивность напряжений при этом составляет 42,6% истинного сопротивления разрыву.
При плоском напряженном состоянии для титанового сплава ВТ2-0 и шарикоподшипниковой стали ШХ15 рассчитаны, построены и проанализированы поверхности разрушения, соответствующие критериям О. Мора, Лебедева-Писаренко и деформационному критерию.
В первом квадранте (область растягивающих напряжений ‑ "жесткие" напряженные состояния) критерии Мора и Лебедева–Писаренко дают результаты с ошибкой не в запас прочности.
С помощью введенного параметра l, характеризующего длину радиус-вектора точки, принадлежащей поверхности разрушения, осуществлено сравнение рассматриваемых критериев.
Во втором, третьем и четвертом квадрантах поверхностей разрушения хрупкого материала критерий Мора и Лебедева – Писаренко дают более консервативную оценку, чем наиболее адекватный деформационный критерий.
В третьем квадранте для пластичного материала критерий Мора дает завышенные оценки разрушающего напряжения. При плоском равноосном сжатии отличие между разрушающими напряжениями, определенными по деформационному критерию и по критерию Мора составляет 30% для титанового сплава ВТ2-0 и 44% для инструментальной стали ШХ15. Причем, если для пластичного материала величины разрушающих напряжений, определенные по деформационному критерию и критерию Лебедева - Писаренко, более консервативны чем оценка Мора, то в случае хрупкого материала оценка, полученная при помощи деформационного критерия значительно «мягче» чем результаты полученные критериями Мора и Лебедева-Писаренко.
Во втором и четвертом квадрантах максимальное отличие оценок по критериям Мора и Лебедева–Писаренко от оценки разрушающих напряжений, предсказываемой деформационным критерием, составляет 23 % для шарикоподшипниковой стали ШХ15 (причем ошибка идет в запас прочности), для титанового
сплава ВТ2-0 это отличие составляет 58 % (с ошибкой идущей не в запас прочности).
Для пластичного материала рассчитаны и проанализированы зависимости интенсивности напряжения в момент разрушения от величины гидростатического давления. Наложение всестороннего гидростатического давления при одноосном сжатии повышает сопротивление материала разрушению.
Интенсивность
разрушающей деформаций при максимальном
гидростатическом давлении
, определенная по критерию Мора, в 3,6
раза выше, чем по деформационному
критерию. Интенсивность напряжений в
момент разрушения по критерию Мора в
1,1 раза выше, чем по деформационному
критерию.
Наложение всестороннего гидростатического давления на одноосное растяжение повышает сопротивление материала разрушению в 1,437 раза по деформационному критерию и в 1,567 раза по критерию Мора.
Деформационный критерий хорошо согласуется с экспериментальными данными и, в отличии от критерия Мора, учитывает влияние всех главных напряжений. Поэтому, деформационный критерий дает более точный результат.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Кононов К.М. Критерии прочности материалов при статическом нагружении: учебное пособие / К.М. Кононов, В.Б. Порошин. – Челябинск: Изд-во ЮУрГУ, 2011.– 30 с.