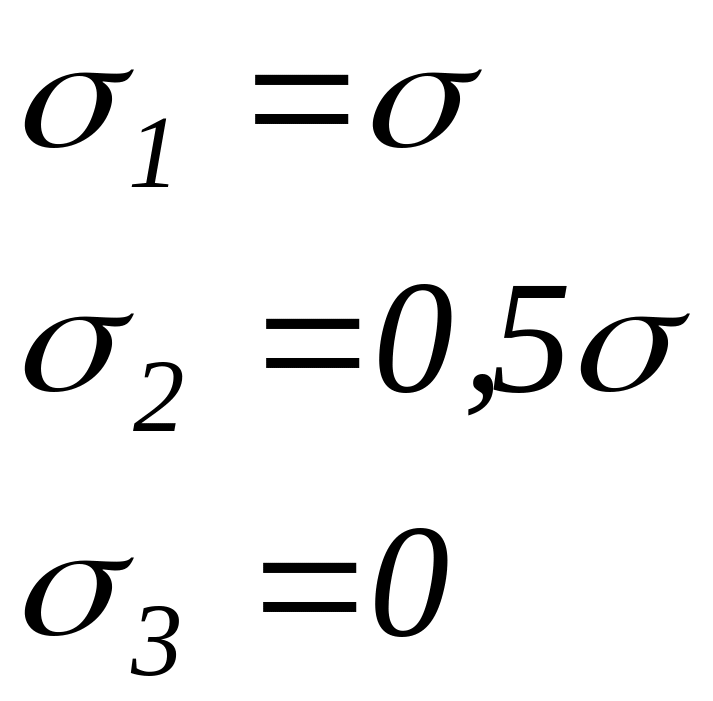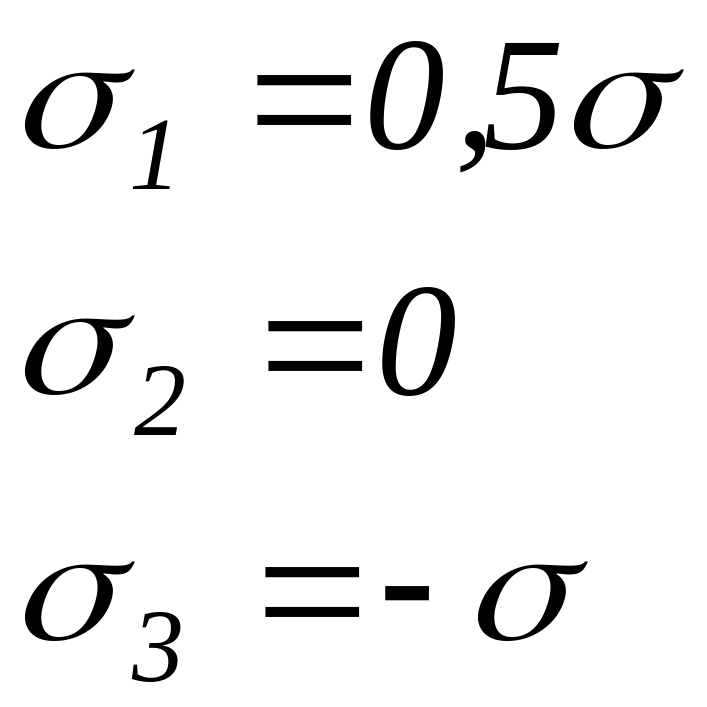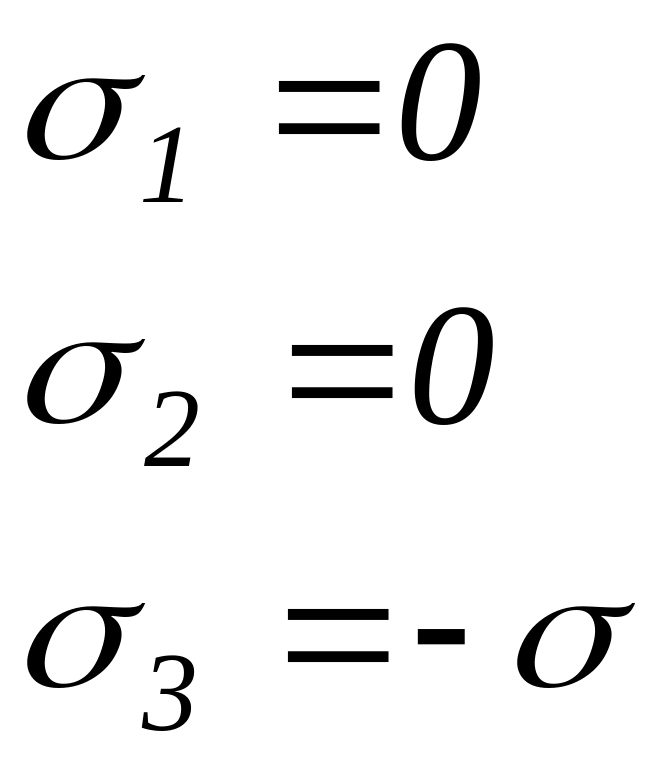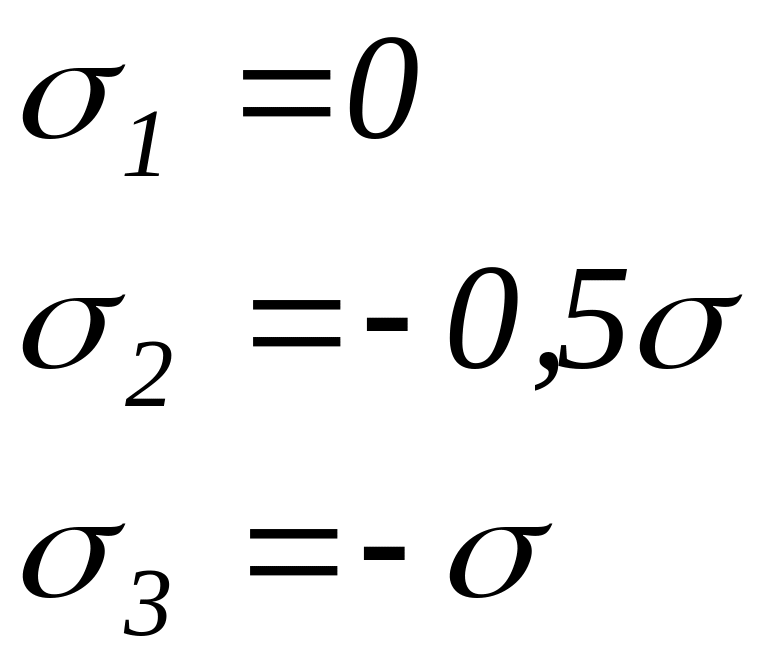3. Поверхности разрушения при плоском напряжённом состоянии для пластичного и хрупкого материалов

3.1. Критерий о. Мора

Теория прочности Мора основана на предположении, что второе главное напряжение оказывает малое влияние на наступление предельного состояния и может не учитываться. Она развивает идею о зависимости прочности как от нормального, так и касательного напряжения.

Эту гипотезу удобно применять для материалов, прочностные характеристики которых при одноосном сжатии отличаются от прочностных характеристик при одноосном растяжении.

В соответствии с теорией О.Мора для определения условия разрушения при сложном напряжённом состоянии используется огибающая окружностей радиусом и координатами центра ; , построенных для предельных напряжений, при которых в опытах при различных напряжённых состояниях наступает разрушение. Считается, что разрушение происходит, если наибольшая окружность Мора для данного напряжённого состояния коснётся огибающей или пересечёт её. Предполагается, что в момент разрушения в опасной площадке (площадка с максимальным касательным напряжением ) величина разрушающего касательного напряжения зависит от величины и знака нормального напряжения, действующего в этой площадке

.

Если огибающую предельных окружностей Мора аппроксимировать прямой, касающейся окружностей, соответствующих растяжению и сжатию , то разрушающее значение максимального касательного напряжения будет линейно зависеть от напряжения . В этом случае условие разрушения при сложном напряжённом состоянии может быть записано в виде

, или

.

Для определения параметров A и B достаточно провести испытания, например, на растяжение и сжатие.

Условие разрушения по критерию О. Мора при сложном напряжённом состоянии имееет вид

, ;

(15)

здесь , – действительное напряжение в момент разрушения при растяжении и сжатии; – коэффициент разнопрочности; – главные напряжения.

Для инструментальной стали ШХ15 (таблица 4)

МПа, МПа, . (16)

Согласно критерию О.Мора, при сдвиге запишем

. (17)

Тогда, используя данные таблицы 2 и зависимость (17) для пластичного материала титанового сплава ВТ2-0, получим

МПа, МПа,

. (18)

Поверхность разрушения строим в относительных координатах . По точкам, соответствующим относительным значениям напряжений и , приведенным в таблице 5, определяем главные напряжения , по критерию Мора (15) рассчитываем эквивалентное напряжение и из условия разрушения (15) получаем координаты точек поверхности разрушения.

Результаты расчета для титанового сплава ВТ2-0 и инструментальной стали ШХ15 представлены в таблице 9 и проиллюстрированы рисунком 3.

Рисунок 3. Поверхности разрушения по критерию Мора

для хрупкого и пластичного материалов

Теория Мора нашла подтверждение в многочисленных опытах над различными материалами. Она отличается определенной широтой: предвидит возможность перехода материала из упругого состояния в пластичное; возможность хрупкого разрушения без заметных пластических деформаций; допускает различное сопротивление материала растяжению и сжатию.

Однако теория Мора обладает серьезными недостатками. Один из них – отсутствие учета второго главного напряжения . Для объёмных напряжённых состояний при растягивающих главных напряжениях теория разрушения Мора может давать большую ошибку при определении разрушающих напряжений вследствие замены криволинейной огибающей прямой линией. Для описания разрушения конструкций из малопластичных и хрупких материалов критерий Мора вполне пригоден.

Таблица 9. Координаты точек поверхностей разрушения титанового сплава ВТ2-0 и инструментальной стали ШХ15 по критерию Мора

Вид напряженного состояния	Главные напряжения	Титановый сплав ВТ2-0			Инструментальная сталь ШХ15
		Эквивалентное напряжение			Эквивалентное напряжение
		1,000	1,000	1,000	1,000	1,000	1,000
		1,000	1,000	0,500	1,000	1,000	0,500
		1,000	1,000	0,000	1,000	1,000	0,000
		1,217	0,822	-0,411	1,242	0,805	-0,402
		1,443	0,698	-0,698	1,485	0,673	-0,673

Таблица 9 (продолжение)

Вид напряженного состояния	Главные напряжения	Титановый сплав ВТ2-0			Инструментальная сталь ШХ15
		Эквивалентное напряжение			Эквивалентное напряжение
		0,933	0,536	-1,072	0,985	0,508	-1,015
		0,433	0,000	-2,308	0,485	0,000	-2,063
		0,433	-1,154	-2,308	0,485	-1,031	-2,063
		0,433	-2,308	-2,308	0,485	-2,063	-2,063