1 Задание на курсовое проектирование [1]

1. Для пластичного материала – титанового сплава ВТ2-0 по значениям приведенных в таблице 1 механических характеристик необходимо получить параметры степенной аппроксимации кривой деформирования в виде

,

где exp(e) ‑ истинное напряжение;

- условное напряжение; при построении соответствующей диаграммы деформирования определяется отношением приложенной нагрузки к начальной площади поперечного сечения образца;

- логарифмическая деформация – сумма упругой и неупругой составляющих; если значение е велики, допустимо принять ;

‑ логарифмическая пластическая деформация; при <10% можно считать, что (максимальное отличие не превышает 0,5%);

- пластическая составляющая деформации (относительное удлинение ε);

K, m – постоянные материала, зависящие от температуры и скорости деформирования.

Таблица 1. Механические характеристики пластичного материала – титанового сплава ВТ2-0

Условный предел текучести	Временное сопротивление	Коэффициент относительного поперечного сужения (в момент разрыва)	Предел прочности при сдвиге	Модуль упругости
840	1000	25	820	1,10

2. В относительных координатах 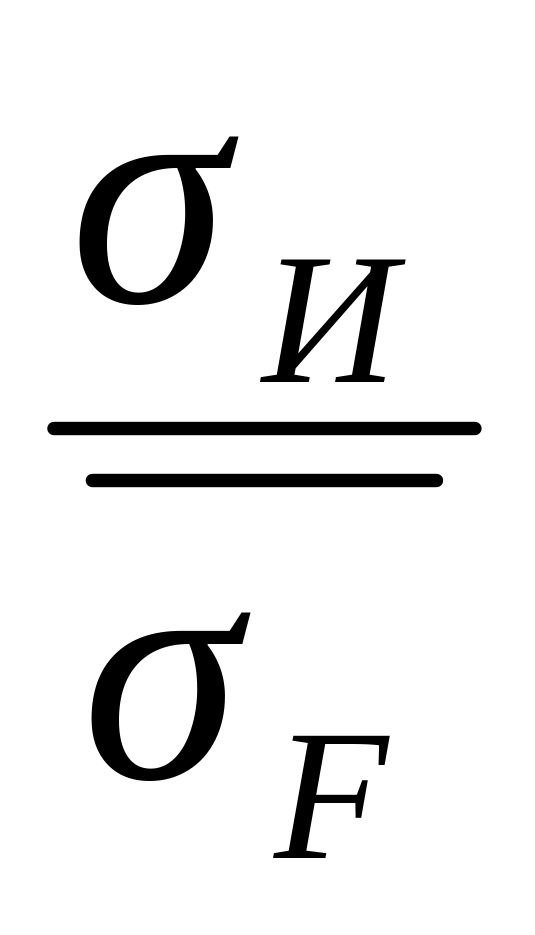~ построить единую кривую деформирования по точкам, соответствующим следующим значениям относительной деформации (таблица 2).

- истинное напряжение при разрушение растягиваемого образца (истинное сопротивление разрыву);

- ресурс пластичности материала, предельная логарифмическая пластическая деформация в момент разрыва образца.

Таблица 2. Значения относительной деформаций для построения кривой деформирования

0,01

0,05

0,10

0,60

1,00

2,00

3,00

4,00

3. На единой кривой деформирования отметить точки, соответствующие предельным значениям интенсивности напряжений и деформаций в момент разрушения, при следующих видах напряжённого состояния: растяжение, сжатие, чистый сдвиг, плоское равноосное растяжение ( ), плоское равноосное сжатие ( ), объёмное растяжение с соотношением компонент , . Виды напряженного состояния с иллюстрациями приведены в таблице 3.

Таблица 3. Виды напряженного состояния

Растяжение		Плоское равноосное растяжение
Сжатие		Плоское равноосное сжатие
Чистый сдвиг		Объемное растяжение

4. Для заданных пластичного и хрупкого материалов, характеристики которых представлены в таблицах 1 и 2, построить поверхности разрушения при плоском напряжённом состоянии, соответствующие трем критериям: О. Мора, Лебедева–Писаренко и деформационному критерию при различных сочетаниях двух главных напряжений σ_x , σ_y . Поверхности строятся по точкам, соответствующим значениям главных напряжений, приведенным в таблице 5.

Таблица 4. Характеристики прочности хрупкого материала – инструментальной стали ШХ15(закалка)

Предел прочности при растяжении	Предел прочности при сжатии	Временное сопротивление сдвигу
2400	4950	2000

Таблица 5. Относительные значения главных напряжений и для построения поверхностей разрушения

	1	1	1	1	1	0,5	0	-0,5	-1
	1	0,5	0	-0,5	-1	-1	-1	-1	-1

5. Для пластичного материала построить зависимость интенсивности логарифмической неупругой деформации в момент разрушения 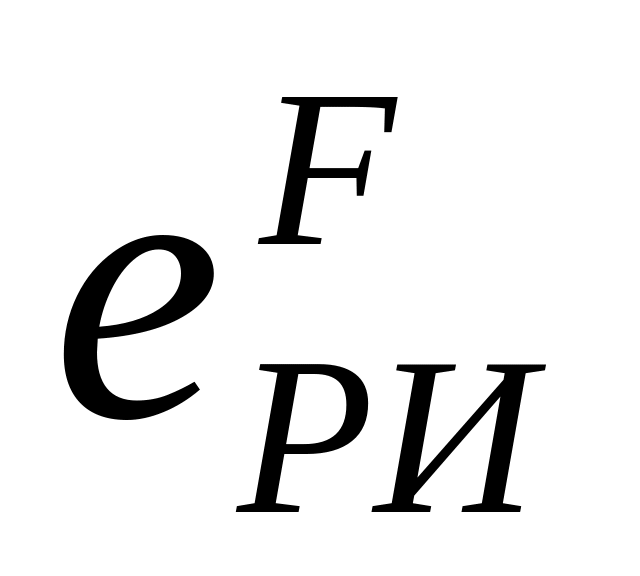и соответствующей интенсивности напряжений от величины гидростатического давления p в сочетании с одноосным растяжением (так моделируется растяжение в камере высокого давления). Зависимость строить по точкам, соответствующим значениям относительного давления, приведенным в таблице 6.

Таблица 6. Величины гидростатического давления p

0,0

0,2

0,4

0,6

0,8

1,0

При построении использовать два критерия разрушения: О. Мора и деформационный критерий.