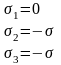3.2 Аппроксимация диаграммы деформирования при сложном напряженном состоянии

На основании многочисленных экспериментальных данных, полученных в условиях пропорционального нагружения, было установлено, что с достаточной для инженерных расчетов степенью точности диаграмму деформирования материала независимо от вида напряженного состояния можно описать с помощью зависимости, получившей название обобщенной кривой деформирования, которая в случае значительных пластических деформаций вполне удовлетворительно аппроксимируется по Рамбергу-Осгуду степенной функцией вида

где и – интенсивности напряжения и логарифмической пластической деформации соответственно, определяемые по формулам

– (10)

– интенсивность напряжения ( – главные напряжения);

– (11)

– интенсивность логарифмической пластической деформации.

При таком их определении значения показателя упрочнения m и коэффициента прочности материала K будут совпадать с величинами, полученными в результате аппроксимации аналогичной степенной функцией кривой деформирования при растяжении.

В ряде случаев (например, при сопоставлении прочностных и деформационных свойств различных материалов) единую кривую удобно представлять в относительных величинах . В такой форме её легко получить, разделив левую и правую часть равенства (9) на соответствующие части выражения (8):

(12)

Графическое представление зависимости (9) приведено на рисунке 3. В таблице 8 представлены значения и соответствующие им значения в расчетных точках единой кривой деформирования.

Рисунок 3. Единая кривая деформирования стали 12Х18Н9 в относительных координатах

Таблица 8. Значения относительных величин и в расчетных точках единой кривой деформирования для стали 12Х18Н9

	0	0,25	0,5	0,75	1	1,2
	0	0,698	0,823	0,906	0,97	1,012

4.Поверхности разрушения стали 12х18н9 при плоском напряженном состоянии

4.1 Критерий о.Мора

Согласно теории Мора для определения условия разрушения используется огибающая окружностей радиусом и координатами центра ; , построенных для предельных значений главных напряжений, при которых в опытах при различных напряженных состояниях наступает разрушение. Считается, что разрушение произойдет, если наибольшая окружность Мора для данного напряженного состояния коснется огибающей или пересечет ее. Таким образом, условие разрушения приобретает вид

. (13)

Если огибающую предельных окружностей Мора аппроксимировать прямой, касающейся окружностей, соответствующих растяжению (радиусом ) и сжатию (радиусом ; – истинное напряжение разрушения при сжатии), то предельное значение максимального касательного напряжения будет линейно зависеть от напряжения величиной , определяющего положение центра соответствующей окружности.

В итоге критерий разрушения О. Мора принимает вид

. (14)

Параметр

(15)

называют коэффициентом разнопрочности.

Из теории прочности Мора следует, в частности, что предел прочности при сдвиге равен

. (16)

Тогда, используя данные таблицы 1, получим

(17)

Очевидным недостатком теории Мора является допущение об отсутствии влияния на прочность второго главного напряжения. Так для объемных напряженных состояний с положительными главными напряжениями критерий Мора может давать значительную ошибку «не в запас» при определении предельных напряжений. Во избежание этого критерий (14) в первом приближении можно дополнить условием, ограничивающим наибольшее главное напряжение. В итоге он будет выглядеть следующим образом :

. (18)

Поверхность разрушения построим в относительных координатах по точкам, соответствующим значениям главных напряжений, приведенным в таблице 9. Результаты расчета относительных эквивалентных и напряжений для стали 12Х18Н9 представлены в таблице 9 и проиллюстрированы рисунком 4.

Таблица 9. Координаты точек поверхности разрушения стали 12Х18Н9 по критерию Мора

Компоненты напряженного состояния	Главные напряжения	Эквивалентное напряжение
		1,000	1,000	1,000
		1,000	1,000	0,5
		1,000	1,000	0
		1,119	0,893	-0,447
		1,239	0,807	-0,807
		0,739	0,677	-1,353
		0,239	0	-4,184
		0,239	-2,092	-4,184
		0,239	-4,184	-4,184