Производная сложной функции
Пусть у нас есть сложная функция: у=u(v(x)). Эту сложную функцию (или функцию от функции) можно представить в виде элементарных функций, которые являются её промежуточными аргументами. Сложная функция дифференцируется по следующему правилу:
Если функция v(x) имеет производную v’(x), а функция у=u(v) производную у’v=u’(v)в соответствующей точке v, то сложная функция у=u(v(x)) в данной точке х имеет производную у’x, которая находится по формуле: у’x=u’(v)·v’(x)
Например:
Производные высших порядков
Производная
от производной первого порядка называется
производной
второго порядка и
обозначается:
или
.
Производная от производной второго порядка называется производной третьего порядка и т.д.
Физический смысл производной второго порядка заключается в том, что вторая производная от пути S по времени t равна мгновенному ускорению переменного движения:
Задача: Найти скорость и ускорение точки, совершающей гармонические колебания по закону:
где
Дифференциал функции и его геометрический смысл
Дифференциалом функции y=f(x) называется произведение производной этой функции на дифференциал аргумента dx или на приращение аргумента ∆х:
dx≈∆x
Для объяснения геометрического смысла дифференциала функции обратимся к рисунку 1. Из треугольника МОС находим:
ОС=МС tg=x yx.
Но из определения дифференциала функции: yxx=dy, следовательно,
ОС=dy.
Таким образом, отрезок ОС, равный дифференциалу функции, геометрически представляет собой приращение ординаты касательной к графику функции в точке с абциссой x при переходе от точки касания в точку с абциссой (x+x).
Полный дифференциал функции
Пусть дана функция nпеременных:
Z = f (x, y, …, t)
В
этом случае вводится понятие частной
производной:
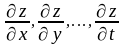
Частной
производной функции Z=f
(x, y) по
аргументу х
называется предел отношения приращения
функции, когда изменяется х,
к приращению аргумента 
х,
когда приращение аргумента стремится
к нулю (
х
→ 0)
Соответственно
частная производная по y
обозначается
.
Если частную производную от функции Z = f(x, y) по х умножить на ее дифференциал dx, то получим частный дифференциал по аргументу х:
Частный
дифференциал по
у будет
равен:
Сумма
частных дифференциалов определяет
полный дифференциал функции
Полный дифференциал для функции двух переменных Z = f(x, y) равен:
Применение понятия дифференциала функции в приближённых вычислениях
При достаточно малых |x| выполняется условие: y dy.
Учитывая, что y = f(x0+x)-f(x0),
dy =f(x0)x, получаем
f(x0+x)-f(x0) f(x0)x, откуда
f(x0+x) f(x0)+f(x0) x (*)
Например:
Вычислить приближённо
.
Решение:
,
тогда x0
=25, x=2.
Применяя формулу (*), получаем:
Эталоны решения типовых задач
Задача
1(а). Найти
производную функции:
.
Решение:
Для решения
задачи необходимо применить правило
дифференцирования алгебраической
суммы:
и формулу производной степенной
функции:
.
Тогда получим:
Ответ:
Задача
1(б). Найти
производную функции:
Решение:
Применяя правило дифференцирования
произведения функций
,
находим
Ответ:
Задача
1(в) .Найти
производную функции:
;
x2-1≠0.
Решение:
Применяя
правило дифференцирования частного
функций:
;
v≠0
находим:
Ответ:
Задача
2(а). Найти
производную функции:
.
Решение:
Данная функция
может быть представлена в виде сложной
степенной функции:
.
В
соответствии с формулой производной
сложной степенной функции:
,
имеем:
.
Ответ:
Задача
2(б). Найти
производную функции:
Решение:
Применяем
правило дифференцирования сложной
функции:
и имеем:
Ответ:
Задача
2(в). Найти
производную функции:
.
Решение: Данная функция является сложной и её производная определится следующим образом:
.
Ответ:
.
Задача
3(а). Найти
производную второго порядка от функции:
.
Решение:
Находим первую
производную:
.
Зная, что производной второго порядка называется производная от производной первого порядка, получаем:
Ответ:-
Задача 3(б). Точка движется по закону: x=t–sint. Определить мгновенные скорость и ускорение точки.
Решение:
Мгновенная
скорость точки характеризуется первой
производной от смещения x
по времени t:
.
Мгновенное ускорение точки характеризуется
второй производной от смещения x
по времени t
или первой
производной от скорости по времени:
.
Ответ:
;
.
Задача
4. Определите
зависимость градиента концентрации от
координаты, если зависимость концентрации
от координаты задана функцией:
,
где k
- константа, а C0
есть концентрация вещества при x=0.
Решение:
Величина
градиента концентрации определяется
выражением
и характеризует быстроту изменения
концентрации при изменении координаты.
Пользуясь правилом дифференцирования
сложной функции:
,
в данном случае получим:
.
Ответ: величина зависимости градиента концентрации от координаты
.
Задача
5. Найти
дифференциал функции:
.
Решение:
По определению
,
т.е. чтобы найти дифференциал одной
переменной, нужно найти производную
и умножить её на дифференциал аргумента
dx.
Искомый дифференциал будет:
Ответ:
.
Задача 6.Найти полный дифференциал функции:
Z=3x2y3+8xy2-3y+ex.
Решение:
Применение понятия дифференциала для приближенных вычислений.
Степенная функция: y=xn=(x0±∆x)n, где n любое действительное число.
Если х0=1, то
Задача
7:
Вычислить
;
Решение:
Ответ: 2,016; 1,07
Показательная функция: у=ах
Задача: Вычислить 42,1
Решение:
Ответ: 42,118,37