
- •Гидравлика
- •Основные характеристики турбулентного движения
- •Основные уравнения переноса субстанций
- •2.Перенос энергии (теплоты) - закон Фурье:
- •3.Перенос импульса:
- •Уравнение неразрывности потока
- •Моделирование химико - технологических процессов
- •Гидромеханические процессы
- •Давление покоящейся жидкости на дно и стенки сосуда
- •Уравнение Бернулли
Моделирование химико - технологических процессов
Многие химико-технологические процессы настолько сложны, что описывающую их систему дифференциальных уравнений решить известными в математике методами не представляется возможным. В таких случаях используют метод моделирования. Под моделированием понимают исследование объектов на их моделях. Моделирование широко применяется как в научных исследованиях, так и в решении задач. Моделирование осуществляется 2-мя основными методами:
методом теории подобия – физическое моделирование, и
методом численного эксперимента - математическое моделирование.
Физическое моделирование ( метод обобщенных переменных ). Здесь одним из основных принципов теории подобия является выделение группы подобных явлений.
Подобные явления – те, для которых отношения сходственных и характеризующих их величин постоянны .Выделяют 4 вида подобия: геометрическое, временное, физических величин, начальных и граничных условий.
н атура
атура
![]() константа
геометрического подобия.
константа
геометрического подобия.
модель
В ременное подобие предполагает, что сходственные точки подобных систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отношения которых = const.
П![]() одобие
физических величин –
означает, что отношение физических
величин двух любых сходственных точек
или частиц подобно размещенных в
пространстве и времени, величина
постоянная.
одобие
физических величин –
означает, что отношение физических
величин двух любых сходственных точек
или частиц подобно размещенных в
пространстве и времени, величина
постоянная.
П![]() одобие
начальных и граничных условий
предполагает, что начальное состояние
и состояние на границах системы (натуры
и модели) подобны, т. е. отношения основных
параметров в начале и на границах систем
постоянны. (справедливо, когда есть
геометрическое временное и физическое
подобие)
одобие
начальных и граничных условий
предполагает, что начальное состояние
и состояние на границах системы (натуры
и модели) подобны, т. е. отношения основных
параметров в начале и на границах систем
постоянны. (справедливо, когда есть
геометрическое временное и физическое
подобие)
Безразмерные числа i, выражающее отношение 2-х однородных величин в подобных системах, называются инвариантами подобия (i).
Отношения однородных величин – называются симплекс.
![]()
![]() - геометический
симплекс.
- геометический
симплекс.
Инварианты подобия, выраженные отношением разнородных величин – называются критериями подобия. (Re – число или критерий подобия).
Можно получить критерии для любого физического явления.
Критерия подобия – безразмерны.
Подобные между собой явления характеризуются численно равным критериями подобия – это условие подобия процессов.
Если критерии подобия найдены из условий однозначности, то они называются определяемыми.
Критерии, в которые входит искомая величина называется определяющими.
С истема дифференциальных уравнений может быть представлена в виде зависимости между критериями подобия. f(k1, k2,…)=0. – критериальное уравнение.
Т.о, теория подобия дает возможность представить решение дифференциального уравнения в виде обобщенных критериальных уравнений.
Г идродинамическое
подобие. Запишем
уравнение Н-С для оси z..
идродинамическое
подобие. Запишем
уравнение Н-С для оси z..
![]()


Е![]() сли
движение установившееся, то
сли
движение установившееся, то
Т![]() огда
огда
З![]()
 аменим
дифференциалы конечными величинами,
l–
определяющий размер
аменим
дифференциалы конечными величинами,
l–
определяющий размер
![]() - о
тражает
силы тяжести ;
- о
тражает
силы тяжести ;
![]() - силы трения;
- силы трения;
![]() -
силы инерции;
-
силы инерции;
![]() -
отражает силы давления;
-
отражает силы давления;
Разделим члены одной части уравнения на члены другой части. Получим критерии подобия
1)![]()

к![]() р.
Фруда, но чтобы избежать чисел <1 к
р.
Фруда называют величину
р.
Фруда, но чтобы избежать чисел <1 к
р.
Фруда называют величину
К
![]() р.
Fr-
отражает
влияние силы тяжести на движение
жидкости.
р.
Fr-
отражает
влияние силы тяжести на движение
жидкости.
2)
к![]()
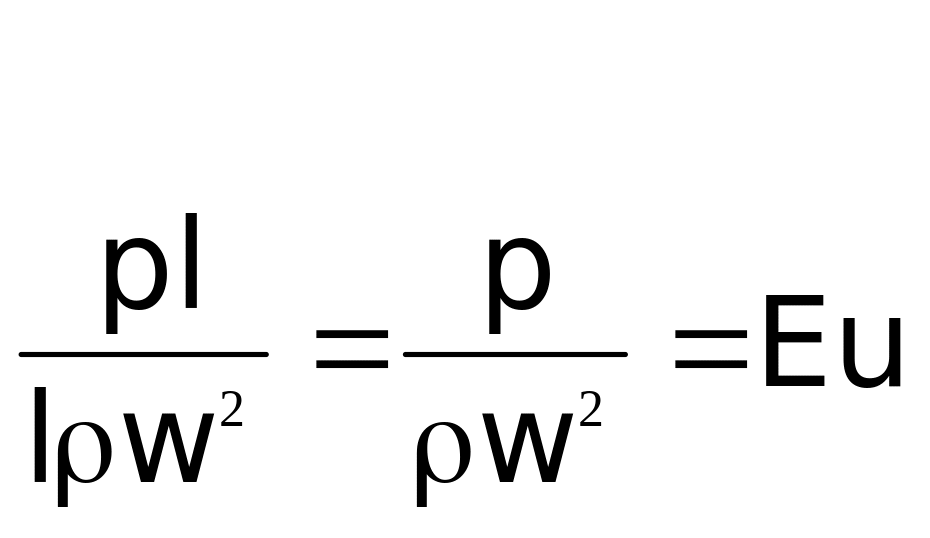

![]() р.
Эйлера. Обычно вместо
р.
Эйлера. Обычно вместо
к![]() р.
Эйлера отражает влияние
перепада гидростатического давления
на движение жидкости.
р.
Эйлера отражает влияние
перепада гидростатического давления
на движение жидкости.
3)
к![]()
![]() р.Re
– отражает влияние
силы трения на движение жидкости
р.Re
– отражает влияние
силы трения на движение жидкости
Решение уравнения Н-С, описывающее в общем виде процесс движения жидкости, может быть представлен критериальным уравнением вида:
![]()
![]() Кр. Галилея .
Кр.Архимеда
Кр. Галилея .
Кр.Архимеда
![]()
