Скалярний добуток векторів

Кутом між двома векторами називається кут між їх напрямами.

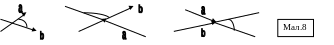
Скалярним добутком двох ненульових векторів називається число, що дорівнює добутку довжин цих векторів на косинус кута між ними, тобто

.

Якщо один з цих векторів нульовий, тоді їх добуток вважається рівним 0.

Скалярний добуток позначається та називається скалярним квадратом; .

З означення скалярного добутку випливає: якщо вектори перпендикулярні, то їх скалярний добуток дорівнює 0. Навпаки: якщо скалярний добуток векторів дорівнює 0, то вектори перпендикулярні:

.

Якщо вектори задані з своїми координатами, тоді скалярний добуток можна обчислити за формулами: ; .

Приклад 5.

В рівносторонньому трикутнику АВС сторона дорівнює 6см. Знайти скалярний добуток векторів: а) та ; б) та .

Розв'язання.

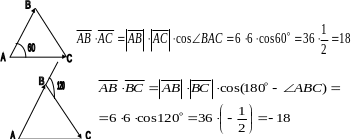
Відповідь: а) 18, б) – 18.

Приклад 6.

Дано: . Знайти .

Розв'язання.

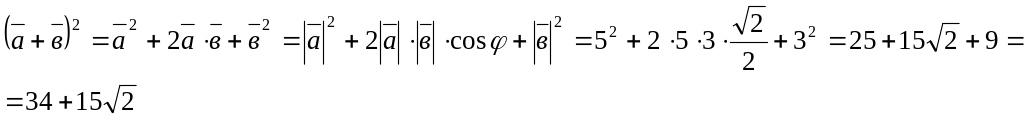Відповідь: .

Приклад 7.

Які з даних пар векторів взаємно перпендикулярні: ?

Розв'язання.

Відповідь: .

Знаходження кута між векторами

За означенням скалярного добутку . Тоді

.

Приклад 8.

Обчислити кут між векторами .

Розв’язання.

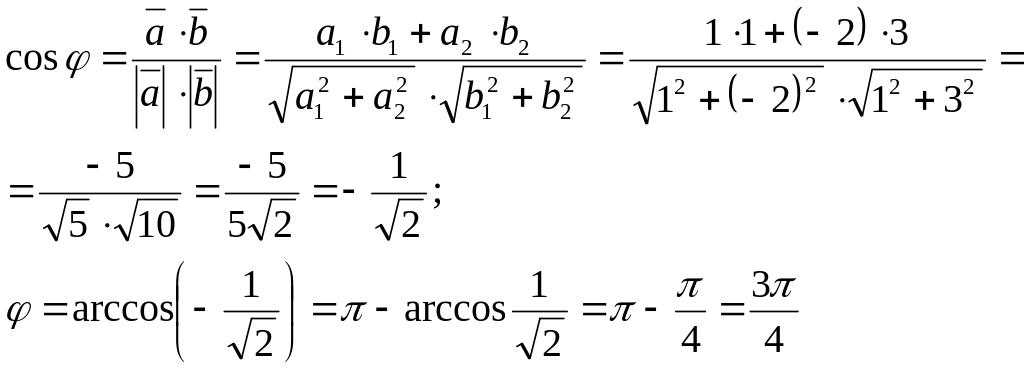
Відповідь: .

Приклад 9. Знайти кути трикутника АВС, якщо А(6;7), В(3;3), С(1;-5).

Розв’язання.

1)

2)

3) Тоді

Відповідь: .

Ділення відрізку в заданому відношенні

Якщо точка М ділить відрізок між точками та у відношенні (мал.9), тоді координати точки ділення М обчислюються за формулами:

; ; .

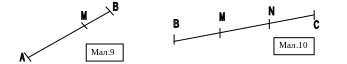
Якщо точка М ділить відрізок АВ навпіл, тоді і координати точки М обчислюються за формулами:

; ; .

Приклад 10.

Дано точки В(-1;3) та С(8;-12). Знайти координати точок М та N, які поділяють відрізок ВС на три рівні частини (мал.10).

Розв’язання.

Точка N поділяє відрізок ВС у відношенні , тоді ;

; тобто N(5;-7).

Точка М поділяє відрізок ВN навпіл, тоді ;

, тоді М(2;-2).

Відповідь: М(2;-2), N(5;-7).

Приклад 11.

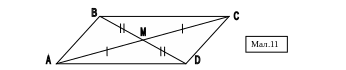
Дано три вершини А(-1;2), В(4;3) та С(7;5) паралелограму АВСD. Обчислити координати вершини D.

Розв’язання.

Діагоналі паралелограму АВСD (мал.11) точкою М поділяються навпіл, тобто точка М – середина відрізків АС та ВD. Знайдемо координати точки М:

та , отже М(3;3,5).

Але , тоді і

. Отже , D(2;4).

Відповідь: D(2;4).

Проекції вектора на вісі координат

Розглянемо вектор з початком в центрі координат та кінцем в точці А(х;у) (мал.12).

Щоб знайти проекції та вектора треба використати формули:

та , при заданому куті нахилу вектора до вісі ОХ.

Приклад 12.

Дано А(5;-2) та В(-3;4). Знайти кут нахилу вектора до вісі абсцис.

Розв’язання.

Знайдемо довжину відрізку : .

За мал.13 проекція дорівнює: ; аналогічно,

. Тоді .

Розв’яжемо систему рівнянь:

Відповідь: .

Приклад 13.

Три сили F₁, F₂, F₃ прикладені в одну точку таким чином, що кут між F₁ и F₂ дорівнює 30°, а між F₂ и F₃ – 60°. Знайдіть їх рівнодіючу силу, якщо | F₁ | = 2 Н,

| F₂| = 10 Н, | F₃ | =11 Н.

Розв’язання.

Розглянемо мал.14: при додаванні векторів та за правилом паралелограма отримаємо прямокутник . Для використаємо теорему Піфагора: .

За правилом паралелограма додамо вектори та , результатом буде результуюча трьох сил . Для знаходження її числового значення використаємо теорему косинусів у : .

Але . При паралельних прямих та кути відповідні, тобто .

З знайдемо : . Тоді , , отже

. Остаточно: .

Відповідь: 19,26Н.

Приклад 14.

Довести, що трикутник з вершинами А(2;2), В(-1;6) та С(-5;3) – прямокутний.

Розв’язання.

Знайдемо довжини сторін трикутника АВС:

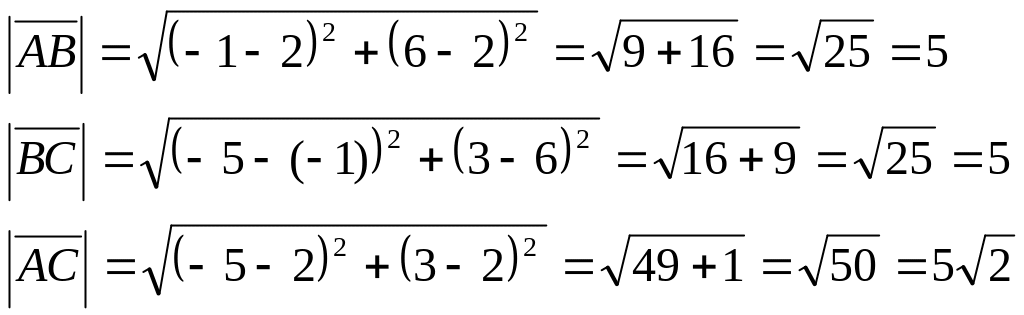
Скористуємося оберненою теоремою Піфагора: якщо в трикутнику сума квадратів двох сторін дорівнює квадрату більшої сторони, тоді цей трикутник прямокутний і навпроти більшої сторони лежить прямий кут. Так як , тоді прямокутний та .

Відповідь: доведено.