МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

МАРІУПОЛЬСЬКИЙ КОЛЕДЖ ДВНЗ «ПДТУ»

МЕТОДИЧНИЙ ПОСІБНИК

ДЛЯ САМОСТІЙНОЇ РОБОТИ

З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ:

«ВИЩА МАТЕМАТИКА»

ДЛЯ СТУДЕНТІВ 2 КУРСУ

Розробила Карбан Н.В.

Розглянуто і затверджено

на засіданні циклової

комісії _____________

Голова циклової комісії

Карбан Н.В.

Для викладачів математики

та студентів.

Загальні методичні вказівки

Даний посібник надає можливість студентам середніх спеціальних навчальних закладів правильно організувати їх самостійну роботу в оволодінні системою знань, умінь та навичок в обсязі діючої програми.

Ця робота вимагає не тільки великої наполегливості, але й уміння, без якого витрата сил та часу не дає потрібного ефекту. Читати, розуміти прочитане та застосовувати його практично – це зміст вміння працювати з навчальними посібниками.

Передусім необхідно ознайомитись зі змістом програми, даної для само опрацювання. Потім слід обрати з наданої літератури основний навчальний посібник чи підручник, за яким буде опрацьована теоретична частина тієї чи іншої теми.

Розв’язання задач є найкращим способом закріплення матеріалу. Загального алгоритму розв’язання всіх математичних задач не існує, але можна виділити певні рекомендації:

1) величини, задані в умові задачі, необхідно перевести в одну систему

одиниць;

2) уважно вивчити мету та питання в задачі, які теоретичні положення

пов'язанні з нею;

3) обміркувати умову та знайти план розв'язання;

4) порівняти задачу з типовими, розв’язання яких вам вже відомі;

5) послідовно дати відповіді та запитання: що дано; що необхідно знайти; чи достатньо даних, щоб знайти невідомі, та т. п.;

6) виконати алгоритм розв’язання та зробити перевірку;

7) обміркувати, чи не має ця задача іншого, більш раціонального розв’язання;

8) якщо ви не можете розв’язати задачу, звернутися до навчальної літератури, в якій може міститися розв'язана задача, схожа на дану; спробуйте використати її для розв’язання.

Література

1. Лисичкин В. Т., Соловейчик И. Л. Математика: учеб. пособие для техникумов. – М.:Высш. шк., 1991. – 480с.

2. Зайцев И. Л. Элементы высшей математики для техникумов. М., 1974г. 416стр.

3. Богомолов Н. В. Практические занятия по математике: Учеб. пособие для

техникумов. – М.: Высш. шк., 1990 – 495с.

4. Алгебра и начала анализа / Под ред. Г. Н. Яковлева. М., 1981, ч. II.

Вектори і координати на площині та в просторі.

Програма

Векторні величини. Вектори. Дії з векторами (додавання векторів, множення вектора на число, скалярний добуток векторів). Розклад вектора. Прямокутні координати на площині та в просторі. Ділення відрізку в даному відношенні. Застосування векторів для розв’язання прикладних задач.

Методичні вказівки

1. Вивчити навчальний матеріал за підручником В. Т. Лисичкин, И. Л. Соловейчик "Математика" розділ 3.

2. Ознайомитися з методичними вказівками до даної теми та розібрати розв’язання прикладів з даного посібника.

3. Дати відповіді на питання та виконати вправи для самоперевірки.

Поняття вектора

Деякі фізичні величини (сила, швидкість, прискорення та інші) характеризуються не тільки числовим значенням, але й напрямом. Наприклад, для характеристики руху тіла в даний момент часу, недостатньо сказати, що воно рухається з швидкістю 50км/год, потрібно ще вказати напрям його руху, тобто напрям швидкості. В зв’язку з цим указані фізичні величини зручно зображати напрямленими відрізками. Такий спосіб зображення фізичних величин відрізняється наочністю.

Напрямлений відрізок називається вектором. Термін «вектор» походить від латинського слова «vector», що в перекладі – «нести», «вести» або «переносити».

Для позначення векторів користуються прописними латинськими літерами, над якими ставлять стрілки або риски: .

Іноді вектор позначають двома великими літерами кінців відрізку, що зображає вектор. Наприклад, вектор на мал.1 можна позначити , де А – початок, В – кінець вектора.

Вектор називають нульовим, якщо його початок співпадає з кінцем. Наприклад, є нульовими векторами.

Довжиною вектора або абсолютною величиною вектора, або модулем вектора називається довжина відрізка, який зображає вектор. Наприклад, , тобто абсолютна величина нульового вектору дорівнює 0.

Два ненульових вектора називають колінеарними, якщо вони лежать на

одній прямій або на паралельних прямих (див. мал.2).

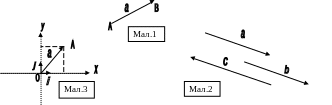
Два колінеарних вектора з одним напрямом називають спів напрямленими, а з різними напрямами – протилежно напрямленими. Наприклад, на мал.2 вектори та - співнапрямлені, а вектори та - протилежно напрямлені.

Нульовий вектор вважається колінеарним любому вектору.

Одиничним вектором або ортом називається вектор одиничної довжини.

Два вектори називаються рівними, якщо вони спів напрямлені та мають однакову довжину. Наприклад, вектори та не рівні, бо хоч мають одну довжину, але мають різні напрями.