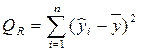- •1. Эконометрическое исследование: определение, задача, цель. Назначение эконометрических моделей.
- •2. Схема проведения эконометрических исследований (краткая характеристика каждого этапа).
- •3. Принципы спецификации эконометрических моделей.
- •4. Типы переменных в эконометрических моделях. Типы экономических моделей (примеры).
- •5. Структурная и приведённая формы спецификации эконометрических моделей (на примере макромодели).
- •6. Классическая парная регрессионная модель (определение и спецификация модели).
- •7. Оценка параметров парной регрессионной модели методом наименьших квадратов (суть метода, вывод формул для нахождения оценок коэффициентов через систему нормальных уравнений).
- •8. Матричная форма метода наименьших квадратов: спецификация парной регрессионной модели в матричной форме, необходимые условия экстремума в матричном виде, вывод оценки вектора параметров модели.
- •9. Теорема Гаусса-Маркова (формулировка, смысл условий и вывода).
- •10. Линейная модель множественной регрессии. Порядок её оценивания методом наименьших квадратов в Excel. Смысл выходной статистической информации функции линейн.
- •11. Алгоритм проверки значимости регрессоров во множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки.
- •14. Алгоритм проверки адекватности множественной регрессионной модели.
- •15. Гетероскедастичность случайного возмущения: определение, причины, последствия, количественные характеристики вектора случайных возмущений в условиях гетероскедастичности.
- •16. Автокорреляция случайного возмущения: определение, причины, последствия, количественные характеристики вектора случайных возмущений в условиях автокорреляции.
- •18. Проблема мультиколлинеарности в моделях множественной регрессии. Виды мультиколлинеарности, признаки, последствия. Методы устранения мультиколлинеарности.
- •20. В чем состоит задача эконометрики?
- •21. Принципы спецификации модели.
- •22. Эндогенные переменные модели конкурентного равновесного рынка
- •23. Экзогенные переменные модели конкурентного равновесного рынка
- •24. Группа предопределённых переменных
- •25. Структурная и приведённая форма модели
- •26. Структурная форма спецификации модели конкурентного рынка
- •27. Оценка ковариации случайных переменных
- •28. Оценка дисперсии случайных переменных
- •29. В чем состоит мнк?
- •30. Эконометрика как наука, определение, основные цели и задачи.
- •31. Этапы построения моделей, их практическое содержание и особенности.
- •32. Базовые понятия эконометрики: экономический объект, переменные объекта, параметры и их взаимосвязи. Примеры экономических моделей.
- •33. Принципы спецификации эконометрических моделей и их содержание.
- •34. Классификация переменных эконометрических моделей.
- •35. Классификация моделей и их формы.
- •36. Формы эконометрических моделей. Переход от структурной к приведенной форме модели.
- •37. Учет случайности характера взаимодействия переменных в экономических объектах. Общий вид эконометрической модели.
- •38. Модели временных рядов, их спецификация.
- •39. Понятие оценки и требования, предъявляемые к оценкам параметров моделей.
- •40. Метод наименьших квадратов, основные понятия и определения.
- •41. Расчет оценок параметров уравнения парной регрессии методом наименьших квадратов.
- •42. Линейный множественный регрессионный анализ
- •43. Проверка значимости множественного уравнения регрессии
- •44. Множественный корреляционный анализ.
- •45. Парные коэффициенты корреляции
- •46. Значимость парных коэффициентов корреляции
- •47. Множественный нелинейный регрессионный анализ
- •48. Линеаризация внутреyнелинейных форм уравнений
- •49. Отличия между регрессионным и корреляционным анализом.
- •50. Задача множественного регрессионного анализа.
- •51. Интерполяция и экстраполяция
- •5 2. Проверка значимости множественного уравнения регрессии.
42. Линейный множественный регрессионный анализ
Задача линейного множественного регрессионного анализа состоит в построении такого уравнения плоскости в (р + 1)-мерном пространстве, отклонение результатов наблюдений уi от которой были бы минимальными. Другими словами, следует вычислить значения коэффициентов b0, b1, …, bp в линейном полиноме
![]() ,
,
Таким образом, чтобы минимизировать выражение
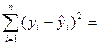
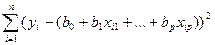 ,
,
где ![]() –
предсказанные значения функции отклика
по модели.
–
предсказанные значения функции отклика
по модели.
Для отыскания минимума указанного выражения необходимо найти частные производные по всем неизвестным коэффициентам b0, b1,…, bp и приравнять их к нулю. Полученные уравнения образуют систему нормальных уравнений
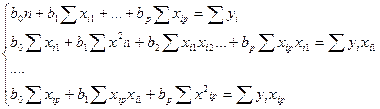
Введем обозначение
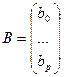 ,
,  и
и 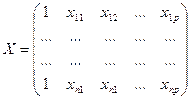 ,
,
тогда систему можно записать в матричной форме
![]() ,
,
где XT – матрица, транспонированная к матрице Х. Для решения системы нормальных уравнений в матричной форме следует умножить ее слева на матрицу, обратную матрице системы нормальных уравнений, если она существует т.е.
![]() ,
,
но ![]() ,
следовательно, столбец коэффициентов
можно найти по выражению
,
следовательно, столбец коэффициентов
можно найти по выражению
![]()
После
определения коэффициентов b0, b1,
…, bp и построения уравнения
регрессии необходимо проверить его
статистическую значимость при помощи
критерия Фишера и статистическую
значимость каждого bi(![]() )
при помощи критерия Стьюдента. При
необходимости можно построить
доверительные интервалы истинных
значений коэффициентов регрессии.
)
при помощи критерия Стьюдента. При
необходимости можно построить
доверительные интервалы истинных
значений коэффициентов регрессии.
Адекватность регрессионной модели можно повысить, увеличивая степень полинома. Однако для полиномов высоких степеней при проведении матричных операций на вычислительной машине накапливаются столь значительные вычислительные погрешности округления, что решение становится практически невозможным. Поэтому обычно ограничиваются построением полинома второго порядка и проведением пошагового регрессионного анализа с включением или исключением переменных.
43. Проверка значимости множественного уравнения регрессии
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
В математической статистике дисперсионный анализ рассмотрен как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.
Обозначим ![]() Согласно
основной идее дисперсионного анализа
Согласно
основной идее дисперсионного анализа
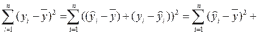
 или
или
![]()
где Q – общая сумма квадратов отклонений зависимой переменной от средней, а QR и Qe - соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
Убедимся
в том, что третье слагаемое  равно
0. Имеем:
равно
0. Имеем:
![]() ,
,
![]() .
.
Теперь
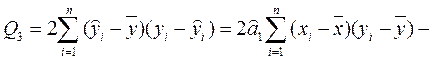

Схема дисперсионного анализа имеет вид, представленный в таблице.
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Средние квадраты |
Регрессия |
|
m-1 |
|
Остаточная |
|
n-m |
|
Общая |
|
n-1 |
|
Средние
квадраты ![]() и
и ![]() представляют
собой несмещенные оценки дисперсий
зависимой переменной, обусловленных
соответственно регрессией или объясняющей
переменной Х ивоздействием
неучтенных случайных факторов и
ошибок; m – число оцениваемых
параметров уравнения регрессии; n –
число наблюдений.
представляют
собой несмещенные оценки дисперсий
зависимой переменной, обусловленных
соответственно регрессией или объясняющей
переменной Х ивоздействием
неучтенных случайных факторов и
ошибок; m – число оцениваемых
параметров уравнения регрессии; n –
число наблюдений.
При
отсутствии линейной зависимости между
зависимой и объясняющими переменными
случайные величины
и
имеют ![]() -
распределение соответственно
с m-1 и n-m степенями свободы,
а их отношение – F- распределение с
теми же степенями свободы. Поэтому
уравнение регрессии значимо на уровне
-
распределение соответственно
с m-1 и n-m степенями свободы,
а их отношение – F- распределение с
теми же степенями свободы. Поэтому
уравнение регрессии значимо на уровне ![]() ,
если фактически наблюдаемое значение
статистики
,
если фактически наблюдаемое значение
статистики
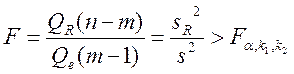 ,
,
где ![]() -
табличное значение критерия Фишера,
определенное на уровне
значимости
при k1=m-1 и k2=n-m степенях
свободы.
-
табличное значение критерия Фишера,
определенное на уровне
значимости
при k1=m-1 и k2=n-m степенях
свободы.
В случае линейной парной регрессии m=2, и уравнение регрессии значимо на уровне , если

Мерой качества регрессионной модели, характеристикой прогностической силы регрессионной модели является коэффициент детерминации, определяемый по формуле

Величина R2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
Так
как ![]() ,
то
,
то ![]() .
.
Чем
ближе ![]() к
единице, тем лучше регрессия аппроксимирует
эмпирические данные, тем теснее наблюдения
примыкают к линейной регрессии. Если
=1,
то эмпирические точки (xi,yi) лежат
на линии регрессии и между переменными
Y и X существует линейная функциональная
зависимость. Если
=0,
то вариация зависимой переменной
полностью обусловлена воздействием
неучтенных в модели переменных, и линия
регрессии параллельна оси абсцисс.
к
единице, тем лучше регрессия аппроксимирует
эмпирические данные, тем теснее наблюдения
примыкают к линейной регрессии. Если
=1,
то эмпирические точки (xi,yi) лежат
на линии регрессии и между переменными
Y и X существует линейная функциональная
зависимость. Если
=0,
то вариация зависимой переменной
полностью обусловлена воздействием
неучтенных в модели переменных, и линия
регрессии параллельна оси абсцисс.
Средняя ошибка аппроксимации
Еще одним показателем качества построенной регрессионной зависимости является средняя ошибка аппроксимации, которая вычисляется по формуле

Эта величина представляет собой среднюю относительную ошибку.