27. Оценка ковариации случайных переменных

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее не известно).

Ковариация служит для характеристики тесноты связи между случайными величинами. Если (x,y) — пара случайных переменных, то их ковариацией называется константа С_ху=Cov(x,y)=E(x·y)-E(x)·E(y)

Свойства математического ожидания позволяют представить С_ху и так: С_ху=E((x-m_x)·(y-m_y)), где m_x=E(x), m_y=E(y)

Для вычисления С_ху нужно знать закон распределения P_xy(q, r) пары (x,y). Если он неизвестен, то ковариацию можно оценить по выборке из генеральной совокупности Ω(x,y): {(x₁, y₁), (x₂, y₂),…,(x_n, y_n)}

Оценкой ковариации служит величина именуемая выборочной ковариацией.

Также тесноту связи определяют при помощи коэффициента корреляции. Существует разные модификации формула данного показателя:

 ,

причем -1≤r_xy≤1

Если |r_xy|=1, то y=a₀+a₁x. Так что при |r_xy|=1 между переменными (x,y) существует жесткая (функциональная) линейная связь.

28. Оценка дисперсии случайных переменных

Оценку дисперсии случайных возмущений можно получить, используя МНК. Для этого должны выполняться предпосылки теоремы Гаусса-Маркова:

ü математическое ожидание случайного возмущения при фиксированном значении предопределенной переменной равно 0

ü дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе (условие гомоскедастичности)

ü ковариация между парами случайных возмущений в наблюдениях =0

ü ковариация между вектором регрессоров и вектором случайных возмущений =0, то есть регрессоры и случайные возмущения независимы.

Оценка ошибки случайных возмущений ищется через дисперсию (согласно теореме Гаусса-Маркова) 

 =   = |   |

На практике применяется не оценка дисперсии, а оценка СКО, как мера адекватности.

В эконометрике важную роль играют две количественные характеристики случайной переменной х: математическое ожидание и дисперсия.

Дисперсия Var(x) – это средний квадрат разброса возможных значений случайной переменной x относительно ее ожидаемого значения:

 

Var (x) =   =E   = 

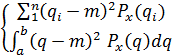
Var(x) – тоже константа, физическая размерность которой равна квадрату физической размерности значений х. Положительный квадратный корень из дисперсии именуется средним квадратическим отклонением (СКО).

Второй предпосылкой теоремы Гаусса-Маркова – дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе.

E ( 

Если, мы имеем одно наблюдение i=1, то получим   и   -это первая выборка. Сделав m выборок, получим набор значений переменной u, которая в каждом наблюдении представляет собой условное распределение. Гомоскедастичность – это ситуация, в которой случайной возмущение подчиняется одному закону распределения.

29. В чем состоит мнк?

Метод наименьших квадратов (МНК, англ. OrdinaryLeastSquares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Пусть   — набор   неизвестных переменных (параметров),  ,  ,   — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым значениям  . По существу речь идет о «решении» переопределенной системы уравнений  ,   в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей   . Таким образом, сущность МНК может быть выражена следующим образом:

.

В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор   в смысле максимальной близости векторов   и   или максимальной близости вектора отклонений   к нулю (близость понимается в смысле евклидова расстояния).