2.7. О корректности поставленной задачи и единственности решения задачи математической физики.

1. Решение должно существовать в каком-то классе функций М₁ .

2. Решение должно быть единственным в некотором классе функций М₂

3. Решение должно нейтрально зависеть от данных задачи (начальных и граничных условий, свободного члена, коэффициентов уравнения).

8. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах.

9. Понятие об общем интеграле уравнения в частных производных.

Рассмотрим практически определение общих интегралов некоторых дифференциальных уравнения в частных производных:

_{Пример 1.} Задана

_и диф. уравнение

_{следовательно} любая произвольная функция - является решением данного уравнения.

_Пример 2. Задано диф. уравнение

_{можно получить решение общего вида}

где _, произвольные дифференцируемые функции.

_Пример 3. Задана

_и диф. уравнение _;

_{проведем замену переменных}

_{найдем частные производные:}

_{получаем уравнение}

_{следовательно} получаем

_{- любая дифференцируемая функция.}

_Пример 4. Задано диф. уравнение

_{проведем замену переменных}

_{найдем частные производные:}

_{уравнение} принимает вид решением является

_{любая дифференцируемая функция .}

_Пример 5 . Задано диф. уравнение

_{проведем замену переменных}

_{уравнение принимает вид}

_{следовательно,} общий интеграл уравнения будет

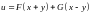
где F и G – любые дифференцируемые функции.

_Пример 6 . задано уравнение

_{решение найдем в виде}

где F и G – любые дифференцируемые функции

Применение общего интеграла к решению некоторых задач математической физики

_{Задано волновое уравнение}

_{обозначим}

_{уравнение примет вид:}

_{общий интеграл волнового уравнения}

_{волна распространяющаяся вправо от начала координат -}

_{волна распространяющаяся влево от начала координат -}

_{Рассмотрим трехмерное волновое уравнение}

_{предположим инвариантность решения от угловых координат θ и φ}

_{замена переменной u=w/r}

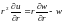
_{в результате получим уравнение}

_{общий интеграл волнового уравнения}

_волна распространяющаяся из бесконечности в точку

_волна распространяющаяся из точки в бесконечность

получим окончательно .

Метод Даламбера для задачи о колебаниях неограниченной струны

Найти функцию , удовлетворяющую уравнению и начальным условиям (задача Коши):

Общий интеграл уравнения имеет вид ;

При 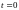будем иметь

Откуда находим или

После подстановки в выражение для получим:

, где .

Легко видеть, что это следует из начальных условий

В итоге получаем формулу, называемую формулой Даламбера:

Раздел 3. Метод Фурье

Метод Фурье является одним из распространенных методов решения уравнений с частными производными и позволяет получить решение задачи в формульном или в общем виде. На практике часто используют приближенные методы решения задач: асимптотические или численные.

1. Уравнения с разделяющимися переменными.

Дифференциальное уравнение называется линейным, если неизвестная функция и все её производные входят в уравнение в первой степени и если оно не содержит членов с произведениями этих величин.

Так, например дифференциальное уравнение второго порядка в частных производных, линейное и однородное относительно неизвестной функции

- линейный дифференциальный оператор,

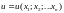
_{уравнение называется неоднородным.}

_{В основе решения таких уравнений лежит принцип суперпозиции:}

_{Если каждая из функций …}

_{Является решением однородного линейного уравнения,}

_{то их линейная комбинация}

_{тоже является решением этого уравнения}. произвольные const.

_{если тогда}

В случае бесконечных рядов принцип суперпозиции допускает обобщение.

_{также является решением этого уравнения, если он сходится к некоторой функции} и допускает почленное дифференцирование.

Обобщенный принцип суперпозиции:

Если каждая из функций является решением однородного дифференциального уравнения, то ряд

_{тоже является решением этого уравнения}. произвольные const.

_{Проверка: тогда .}

_{В случае линейного уравнения в частных производных число слагаемых можно выбрать бесконечно большим, тогда из бесконечно большого множества всегда можно выбрать решения, удовлетворяющие произвольным дополнительным условиям.}

_{Может оказаться, что решение уравнения в частных производных имеет вид то есть зависит от некоторого параметра изменяющегося в конечном или бесконечном промежутке ,то есть при функция является решением уравнения .}

_{cледовательно, любая произвольная функция является решением}

_{Сумма бесконечного сходящегося ряда может быть заменена определенным интегралом:}

_{Этот интеграл тоже является решением уравнения .}

Рассмотрим линейное дифференциальное уравнение с разделяющимися переменными имеющее бесконечное множество решений в виде:

_{Причем все решения} получаются из обыкновенных дифференциальных уравнений подстановкой в

_{Тогда, чтобы переменные в уравнении разделялись, оператор L должен иметь определенную структуру.}

_{Переменные разделяются, если уравнение имеет вид:}

_{L1 зависит только от х1… Lп зависит только от хп, тоесть каждая из частей Li}

_{зависит от одной переменной хi.}

_{Например:}

_.

_{Рассмотрим методику разделения переменных на примере:}

_{Задано уравнение в виде: ,}

_{решение уравнения}

подставим решение в исходное уравнение

Первое слагаемое зависит от х₁ , а второе слагаемое зависит от х₂ равенство возможно только в том случае когда

Исходное уравнение распадается на два уравнения:

Переменные разделены, параметр разделения.

_{Задано уравнение в виде:}

_{решение уравнения}

Исходное уравнение распадается на два уравнения:

3.2. Задача Дирихле для круга. Интеграл Пуассона.